Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME GPK, Department of Machine and Product Design

Supervisor: Dr. Zwierczyk Péter

Strength enhancement and biomechanical development of custom-made acetabular cages

Introducing the research area

Hip joint osteoarthritis is one of the most widespread diseases of our time. Due to increased life expectancy and higher expectations towards the quality of life, including pain-free joint mobility, more people are receiving total hip implants at increasingly younger ages. Parallel to this, the number of replacements for these implants is also rising. One possible indication of this is the development of extensive pelvic bone defects. [1] An image of this can be seen in Figure 1. The research topic is related to the development of implants used for treating such bone defects, the so-called acetabular cages.

 

Figure 1: Healthy pelvis and pelvis with large acetabular bone defect.

 

Brief introduction of the research place

Finite element analyses in biomechanics have a long history at the Department of Machine and Product Design at the Budapest University of Technology and Economics (BME), primarily through the work of Professor Károly Váradi, who supervised numerous diploma theses and doctoral dissertations. The subject matter taught at the department provided a very solid foundation for deepening research in this area.

History and context of the research

The most modern procedure currently used to treat pelvic bone defects, which allows the original pivot point of the hip joint to be restored, is the use of custom-made metal 3D printed acetabular cages. These are custom-made using a virtual reconstruction process, filling the bone gap with a partly solid, partly lattice structure, to fit the patient's anatomy. Their implantation is easy, and the chance of implant fracture is small. The disadvantage is that they are extremely expensive, and a significant amount of metal parts are implanted, which will never transform into living bone. If they have to be removed due to a possible infection, clinical experts will face an even larger bone defect. Dr. Róbert Sződy and his colleagues treated several patients with custom-shaped plate component acetabular cages. [2] Not only did the patients regain their mobility, but the flexible nature of the implant helped the integration of the bone grafts placed behind the acetabular cage. This reduced the degree of bone deficiency, which subsequently allowed for the implantation of a smaller implant. This positive biomechanical effect suggests that it is worth working with such types of implants.

The research goals, open questions

The long-term goal of the research is to develop these acetabular cages. The development will include strength enhancement and related biomechanical development. The strength enhancement is aimed at reducing the stresses in the implant to decrease the likelihood of fracture arising from material fatigue. Biomechanical development refers to the facilitation of the integration and transformation into living bone of the bone grafts placed behind the implant due to mechanical stimulus. For this phenomenon, the implant must be sufficiently flexible, a requirement that goes against the aforementioned strength-related demands. In this way, the problem is reduced to engineering optimization. An indispensable part of the optimization is the knowledge of the loads, in other words, the designer's task includes the determination of those mechanical loads and combinations of loads with which the simulation examination of the acetabular cage can be performed cost-effectively. It should be considered, however, that although the most common lifestyle loads are known, it is not necessarily the same loads that should be used for strength and biomechanical examinations. According to the current standing of the literature, the most frequently selected loads are associated with maximum walking and stair climbing loads, but their use only enables examination for a narrow segment. [3], [4] This kind of loading model should be extended so that computational costs do not increase drastically.

Methods

Modern digital reconstruction, modeling, and simulation methods used in mechanical engineering practice can also be applied to biomechanical analyses. Based on data from computed tomography examinations (CT, a medical imaging tool) a virtual 3D model of the patients' pelvis and implanted prostheses could be created. After accurate geometric modeling, it was possible to simulate the mechanical stresses formed due to loads, using a finite element model. The created virtual models can be seen in Figure 2.

 

 

Figure 2: Geometric and finite element model of the acetabular cage fixation.

 

To ensure that the results provided in this way correspond to reality, the first step was to validate the model, which could be done by using control CT scans.

Biomechanical development includes modeling the transformation of bone grafts. Like bones, bone grafts have the property that their structure strengthens and can become stiffer when subjected to appropriate amounts of mechanical stimuli. Of course, the degradation and stiffness reduction under low loads and overloads can also be modeled. In the current stage of research, this phenomenon, which is known in the literature, has been implemented in the commercial finite element software I used, by a program I have written. To allow for a multitude of simulation runs, it was necessary to automate them, which was done with scripts written in Python and efficient data visualization tools. The transformation of the bone graft is most commonly approached in the literature based on strain energy density, taking into account its average distribution due to loads. The problem here lies in the wide spectrum of loads, the effects of which others have so far been able to approximate only by selecting certain loads. [5] In my research, I used an analytical, mathematical-mechanical derivation with a symbolic mathematical program to determine such equivalent loads and verified the correctness of the derivation with a separate finite element reference calculation.

Results

For strength development, I developed an algorithm that can provide those main load vectors that cover the life-cycle loads, with which the stress concentration locations in the implant can be calculated. The model consistently gave correct results when analyzing the acetabular cages of the examined patients, as deformation or fracture occurred in the zone of the greatest stress predicted by the calculation in the implants. By querying tensile and compressive stress results, even the nature of the deformation can be considered qualitatively correct, as seen from the data derived from the patients' postoperative and one-year control CT examinations. This can be seen in Figure 3, presented for one such load. In the strongly tensioned zones, protrusions are typically observed, while in the strongly compressed zones, dents can be noticed.

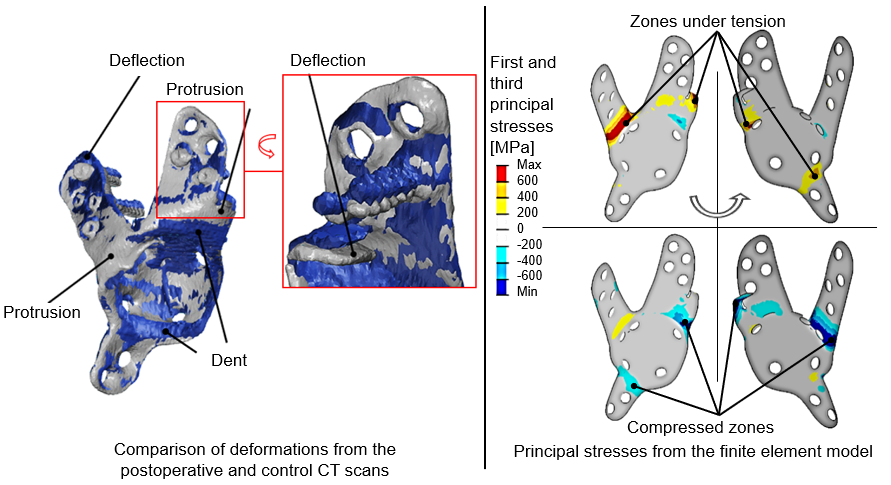
Figure 3: On the left: Deformation reconstructed from the post-operative (blue) and one-year control CT (gray) scans is consistent with the calculated principal stresses (on the right).

 

 

To model the transformation of bone grafts, replacing the multitude of loads, I derived three load vectors in closed form, which provide the same strain energy density distribution in the graft as if it were calculated from the multitude of lifestyle loads. This is presented in Figure 4.

 

 

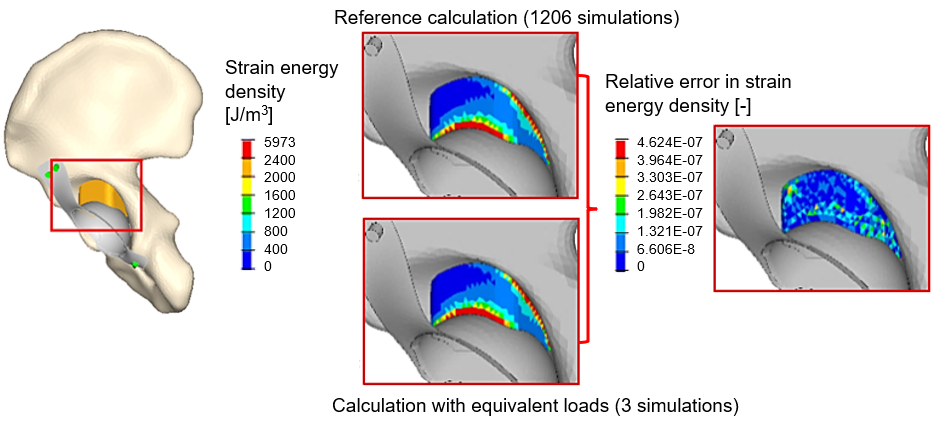
Figure 4: There is only a slight numerical error between the strain energy density calculated by the reference loads and the equivalent load vectors.

 

These loading models clearly introduce a new approach, they improve the loading models that have been widely used in the literature so far and can be used faster to achieve equally accurate or more accurate results.

Expected impact and further research

Each loading model contributes to the evaluation of implant variations, the selection decision, and further implant development. For generating conceptual variations, it is worth using the method of topology optimization, the constraints and objective function of which are related to the mechanical responses to these loads. Figure 5 shows the iterations of a topology optimization run, where a possible shape of the implant is outlined.

 

 

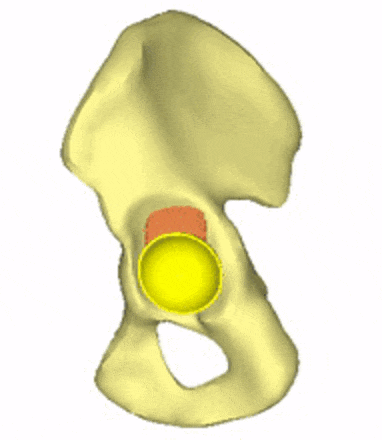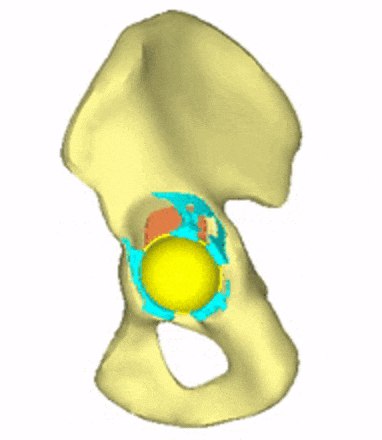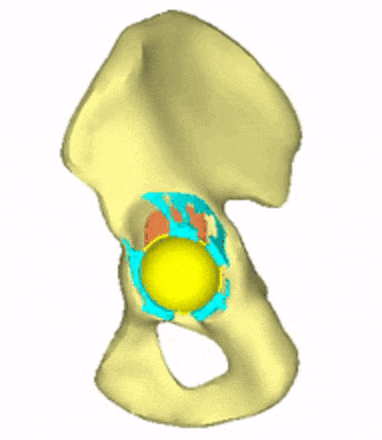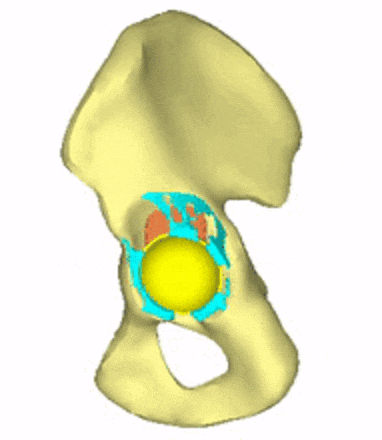
Figure 5: Conceptual design of the acetabular cage from topology optimization.

 

Further research will extend to the application of machine learning models, such as so-called Kohonen maps (self-organizing maps), which can assist in creating conceptual designs for the sheet metal part from the optimization results. Preliminary results from these are also shown in Figure 6.

 

Figure 6: Fitting a self-organizing map to the result of topology optimization.

 

The results of this research will hopefully be beneficial in the future in the form of cost-effective implants that promote the integration of bone grafts.

 

Publications, references, links

List of corresponding own publications (cumulated IF = 10.65):

[Dóczi2018] Dóczi, M; Simonovics, J: Egyedi vápakosaras rögzítés végeselemes modelljének elkészítése. GÉP 69: 3 pp. 8–11, 4 p. (2018)

[Dóczi2020a] Dóczi, M; Zwierczyk, PT; Sződy, R:

Failure analysis of a custom-made acetabular cage with finite element method

In: Steglich, M; Mueller, C; Neumann, G; Walther, M Proceedings of the 34th International ECMS Conference on Modelling and Simulation, ECMS 2020: June 2020, United Kingdom Wilhelmshaven, Germany: European Council for Modelling and Simulation (ECMS) (2020) 408 p. pp. 250–255, 6 p.

[Dóczi2020b] Dóczi, M; Sződy, R; Zwierczyk, PT: Csontgraft változásának végeselemes modellezése HyperMesh-Calculix környezetben GÉP 71: 7-8 pp. 15–18, 4 p. (2020)

[Dóczi2021] Dóczi, M; Zwierczyk, PT; Sződy, R: Implementation of bone graft adaptation's FE model in hypermesh In: Al-Begain, K.; Iacono, M.; Campanile, L.; Bargiela, A. 35th ECMS International Conference on Modelling and Simulation, ECMS 2021 European Council for Modelling and Simulation (2021) pp. 152–156, 5 p.

[Dóczi2022] Dóczi, M; Sződy, R; Zwierczyk, PT: Effect of the Design Constraints and the Loading Model on the Geometry of Topology Optimized Acetabular Cages PERIODICA POLYTECHNICA-MECHANICAL ENGINEERING 66: 3 pp. 253–259, 7 p. (2022)

[Dóczi2023a] Dóczi, M; Sződy, R; Zwierczyk, PT. Equivalent loads from the life cycle of acetabular cages in relation to bone-graft transformation COMPUTER METHODS AND PROGRAMS IN BIOMEDICINE 236 p. 107564 Paper: 107564 (2023)

[Dóczi2023b] Dóczi, M; Sződy, R; Zwierczyk, PT: Extended mechanical loads for the analysis of acetabular cages BIOMECHANICS AND MODELING IN MECHANOBIOLOGY preliminary edition, 13 p. (2023)

 

Table of links:

Own publications (MTMT)

Researchgate profile

BME Department of Machine and Product Design

 

List of references:
[1] Paprosky W, Perona P, Lawrence J (1994) Acetabular defect classification and surgical reconstruction in revision arthroplasty: a 6-year follow-up evaluation. J Arthroplasty 9(1):33–44.

[2] Sződy R, Kotormán I, Manó S, Csernátony Z, Bagi I, Borbás L, Hatos I (2017) Design and manufacturing of custom-made acetabular cages for the revision of hip joint implants: procedure applied in three cases. 7. In: Hungarian conference of Biomechanics, Oct 6–7, Szeged, Hungary

[3] Bergmann G, Deuretzbacher G, Heller M, Graichen F, Rohlmann A, Strauss J, Duda G (2001) Hip contact forces and gait patterns from routine activities. J Biomech 34(7):859–891.

[4] Plessers K, Mau H (2016) Stress analysis of a Burch-Schneider cage in an acetabular bone defect: A case study. Reconstr Rev 6(1):37–42.

[5] Chun BJ, Jang IG (2021) Determination of the representative static loads for cyclically repeated dynamic loads: a case study of bone remodeling simulation with gait loads. Comput Methods Programs Biomed 200:105924.