Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék

Témavezető: Dr. Dombóvári Zoltán

Ipari robotok által megvalósított megmunkálási folyamatok modellezése

A kutatási téma néhány soros bemutatása

Az iparban egyre növekszik az igény arra, hogy iparirobot-karokat fém alkatrészek megmunkálására használjanak, amely felhasználásnak azonban általában magas geometriai pontossági követelményei vannak. Robotok esetén ezen felhasználás során két fontos dinamikai probléma lép fel. Először is a robotkarok a dinamikai hatásokkal szemben – a szerszámgépekkel ellentétben – általában gyenge szerkezetek. Emiatt hajlamosak erősebben nemlineáris tulajdonságokat [H1] mutatni – például ugyanazon rezgés amplitúdó esetében –, amelyek főleg a robotkar csuklóitól és meghajtásától származnak. Az emiatt potenciálisan kialakuló instabil határciklusok még lineárisan stabil megmunkálás esetén is alááshatják a rendszer robusztusságát. Emellett az esztergálás vagy marási eljárások regeneratív folyamatok [H2], vagyis a dinamikai rendszer múltbeli állapotváltozói fontos szerepet játszanak a rendszer hosszú távú viselkedésében. Ennek a tulajdonságnak, illetve a szabályozók időkésései által generált instabilitásoknak már jelentős hatása lehet a megmunkálás minőségére.

A kutatóhely rövid bemutatása

Kutatómunkámat a BME GPK Műszaki Mechanikai Tanszékén végzem. Emellett részt veszek az MTA-BME Lendület Szerszámgéprezgések Kutatócsoport munkájában is, amelynek célja ipari szerszámgépek stabilitásának, illetve robusztusságának fejlesztése. A megmunkálások helyes modellezése fontos a doktori témámban is, ezért a kutatócsoport munkája szoros kapcsolatban van az általam végzett kutatással.

A kutatás történetének, tágabb kontextusának bemutatása

A legelső robotokat legfőképp tárgyak felvételére és áthelyezésére fejlesztették ki [H3], ahol nem volt szükséges kimagasló geometriai pontosságot elérni. Később már használták őket megmunkálási folyamatoknál is, különösen ipari agyag prototípusok gyártására. Ebben az időben a pozícionálási pontosság már egy nagyságrendet fejlődött, amit jobb szenzorok és beépített proporcionális-derivatív visszacsatolású szabályozás segítségével értek el. Ez az elérhető pontosság elegendő volt a korábban említett agyag szoborfelületek esetén, ahol a vágási erők nem különösebben nagyok. Ezt a prototípusgyártási formát lassan átvette a 3D-polimer nyomtatási technológia, néhány esetben azonban manapság is használatosak agyag prototípusok, például autókarosszéria-prototípusok gyártásánál, alacsony költségük és tartósságuk miatt.

Manapság fém alkatrészek ipari robotokkal való megmunkálása nagy lehetőségeket rejt magában, mivel – a szerszámgépekkel ellentétben – sokoldalúak és olcsók. A legtöbb nyílt kinematikai láncú robot kiváló szoborfelületek megmunkálására, továbbá nagy munkatérrel is rendelkeznek. Ennek a sokoldalú konfigurációnak hátránya az alacsony dinamikus merevség, amire fém alkatrészek marása esetén szükség lenne. Ezen felül ezek a szerkezetek hajlamosak erősen nemlineáris tulajdonságokat mutatni, ami veszélyeztetheti a folyamat robusztusságát. Végül a robotok rezgési paraméterei függenek a karok pozíciójától, ezáltal nagy mértékben változhatnak a megmunkálás során, ami nem autonóm matematikai problémához vezet, és fontos szerepet játszhat a rendszer stabilitásának kérdésében.

A kutatás célja, a megválaszolandó kérdések

A kutatás legfőbb célja, hogy az ipari robotokat felkészítse fém alkatrészek megmunkálására, aminek jelen pillanatban jelentős akadályai vannak. A robotok helyes lineáris és nemlineáris jellemzése ugyanolyan fontos, mint a robotmegmunkálás során felmerülő összetett matematikai problémák megfelelő kezelése.

Az általam használt módszerek elsősorban erre a problémára adnak tervezési lehetőségeket, amelyek segítségével lehetőség van a folyamat stabilitásának és robusztusságának biztosítására. A legfőbb problémák közé tartozik a robotok csuklóknál és hajtásoknál jelentkező lehetséges nemlineáris karakterisztikája, a regeneratív hatásból és késleltetett visszacsatolású szabályozókból származó instabilitások, illetve a rendszer bejárt úttól függő időben változó rezgési paraméterei. Ezekre a problémákra először külön-külön kell választ találni, ami végül egy egyesített tervezési és fejlesztési megközelítést eredményezhet. A kutatás során próbálunk a problémákra általános matematikai leírásokat és megoldásokat találni, mivel a vizsgált jelenségek más mérnöki problémákban is előfordulnak.

Módszerek

Gyorsulás-visszacsatolású szabályozás használata a stabilitás és robusztusság javítása érdekében

A tapasztalat az, hogy a megfelelő minőség eléréséhez a robotok dinamikai tulajdonságait javítani kell fémek megmunkálása esetén. Ez viszonylag könnyedén megvalósítható lenne online szabályozással, ami a beépített szabályozó sebesség- vagy gyorsulásjeleit használja fel. Ez egy relatíve egyszerű megoldás lenne, mivel nem szükségesek további költségnövelő berendezések. Problémát jelent viszont, hogy a gyártó biztonsági okokból általában nem ad hozzáférést a már beépített szabályozókhoz, így ezek a mért jelek nem használhatók. Egy másik megközelítés, hogy a végeffektor dinamikus látszólagos merevségét növeljük, passzív vagy szemi-aktív rendszerek használatával. A tapasztalat szerint viszont az ipari felhasználók ódzkodnak ezektől a módszerektől. A már beépített pozicionáló proporcionális-derivatív szabályozó mellett egy további gyorsulás-visszacsatolású szabályozás használata olcsó és egyszerű megoldás lehet a stabilitás és robusztusság javítására. A stabil megmunkálás megvalósításához szükséges az új szabályozó paramétereinek gondos megválasztása és az időkésés helyes szinkronizálása a proporcionális-derivatív szabályozó időkésésével. Elméletileg a robotszerkezet nemlineáris viselkedéséből származó kedvezőtlen hatások is ellensúlyozhatók nemlineáris karakterisztikájú szabályozó segítségével [F1], biztosítva a rendszer robusztusságát.

 

Digitális kontrollerek kvantálásának hatása

A modern digitális kontrollerekben jelenlévő kvantálásnak jelentős hatása lehet a mechanikai rendszer stabilitására. Ez kifejezetten igaz neutrális és siettetett differenciálegyenletek esetén [H4], ahol az állapotváltozók deriváltja függ a múltbéli állapotváltozók deriváltjától vagy második deriváltjától. Az időkésések ezekben a digitális rendszerekben fűrészfogszerű jelekként modellezhetők, amelyek periodikus időkésésfüggvényeket adnak. Az időkésések periodikussága és a lehetséges megmunkálási folyamatok lehetséges periodikussága adja a főperiódust, amely meghatározza a használt numerikus séma szimulációs időintervallumát, amivel a stabilitási tulajdonságok számítása lehetséges.

 

Robotok időben változó rezgési paramétereinek hatása

Az ipari robotok rezgési paraméterei általában erősen függenek a robot pozíciójától, így a megmunkálás során ezek a paraméterek folyamatosan változhatnak a bejárt úttól függően. Az ilyen rendszerek matematikai leírása nem autonóm (általánosan nem periodikus) dinamikai rendszerekhez vezetnek, amelyeknek a paraméterei időben folytonosan változnak. Ezekben a rendszerekben az aszimptotikus stabilitás megvalósítása az egész időintervallumon – például a robot által bejárt teljes pályán – sok esetben nem lehetséges. A véges idejű stabilitás azonban, amely korlátot ad a rezgési amplitúdók legnagyobb lehetséges értékére, megfelelő és teljesíthető követelményt adhat a megmunkálás megfelelő minőségének biztosításához. Ehhez a rezgési amplitúdók pontos becslése szükséges, ami ezen rendszerek esetén nem triviális, és az elérhető numerikus módszerek még a legegyszerűbb esetekben sem adnak megbízható eredményeket. Ezen elvárások szükségessé teszik egy analitikus közelítő módszer megalkotását, amely a későbbiekben akár az új numerikus eljárások verifikálására is megfelelő és ellenőrizhető eredményeket biztosít.

Eddigi eredmények

Hopf-bifurkáció számítása neutrális késleltetett differenciálegyenletekre

Két szabadságfokú nemlineáris robotmodellt késleltetett gyorsulás-visszacsatolású szabályozóval vizsgáltam. Ez tekinthető a legegyszerűbb ekvivalens modellnek, amely a robot nemlineáris tulajdonságait és a nemlineáris késleltetett gyorsulás szabályozót is képes jellemezni. Ezen rendszer mozgásegyenlete neutrális késleltetett differenciálegyenlet, mivel az állapotváltozók deriváltjai függenek múltbeli állapotváltozók deriváltjaitól.

A rendszer lineáris stabilitásvizsgálata után a nemlineáris vizsgálathoz a centrális sokaság redukciót levezettem neutrális egyenletekre [F2]. Ez a kritikus bifurkációs pont közelében lévő periodikus pályák analitikus közelítése. Az eredményeket numerikus követő módszer [H5] segítségével ellenőriztem. Az 1. ábra (c, d) képei mutatják, hogy a nemlineáris kontrolparaméterek helyes megválasztásával stabil határciklusok biztosíthatók, ami a rendszer robusztusságát javítja.

 

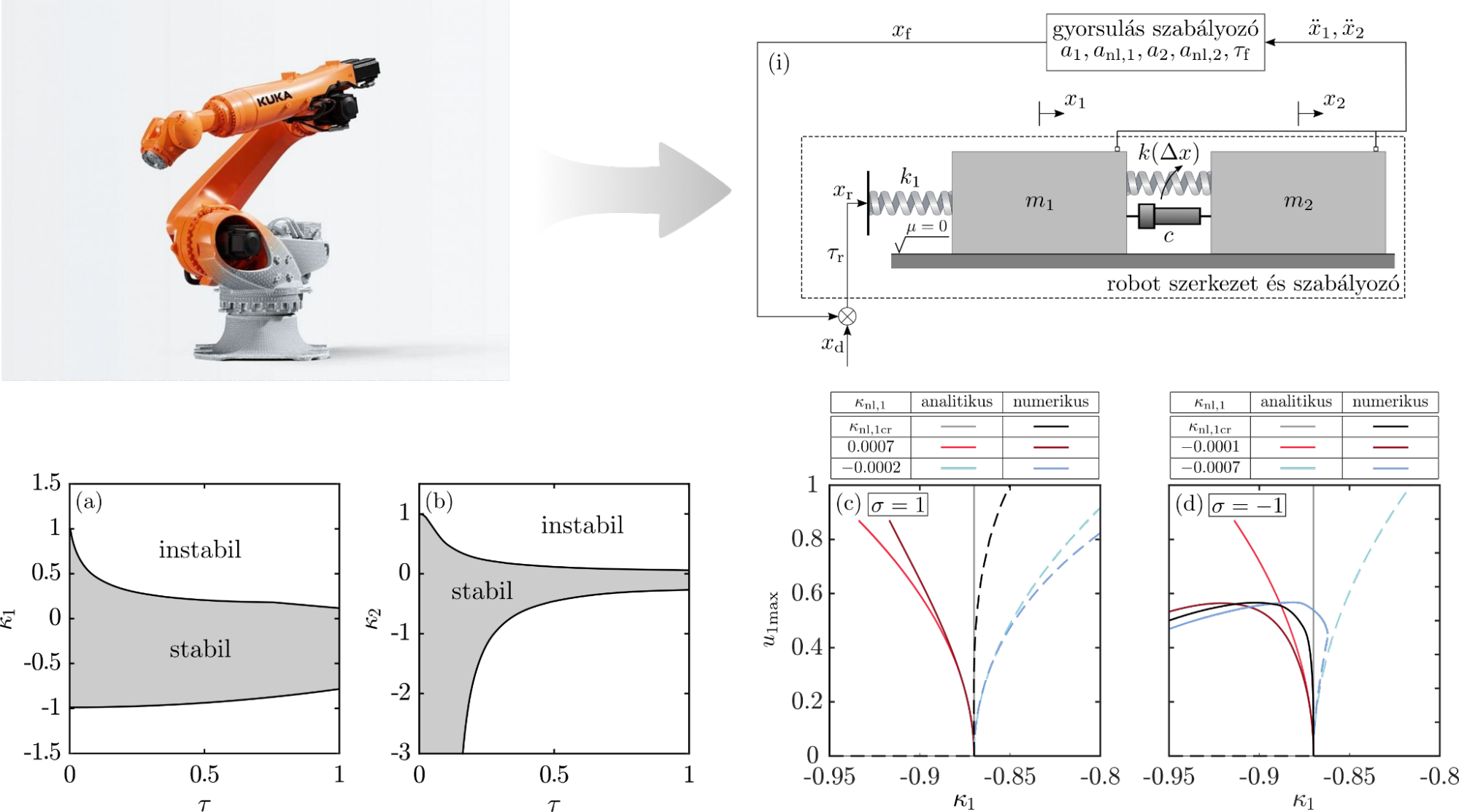
1. ábra: (i) két szabadságfokú robot modell. (a, b) lineáris stabilitás vizsgálat. (c, d) analitikus és numerikus eredmények bifurkációs eredmények felkeményedő (c) és kilágyuló (d) merevségre

 

Robotokkal való megmunkálások stabilitása digitális szabályozók esetén

A szemidiszkretizáció módszere [H6] alkalmas időkésleltetett rendszerek stabilitásának számítására. Ezt a módszert egy programcsomagban általánosítottam, amely alkalmas kvantált és folytonos időkésések kezelésére, illetve retardált, neutrális és siettetett egyenleteket is kezel. A numerikus módszert két mérnöki alkalmazáson keresztül ellenőriztem.

Elsőként egy önvezető autó hierarchikus szabályozásának stabilitásvizsgálatát végeztem el. Az eredményeket futópados méréssekkel is igazoltam egy kis skálájú modellen [F3]. Ezután robotkarral való marási megmunkálás stabilitását vizsgáltam, ahol a beépített digitális proporcionális-derivatív szabályozó mellett digitális gyorsulásszabályozás is van. Ez siettetett rendszert eredményez. A 3. ábrán látható, hogy megfelelő gyorsulásszabályozó-késéssel a rendszer stabilitása javítható [K2, F4].

 

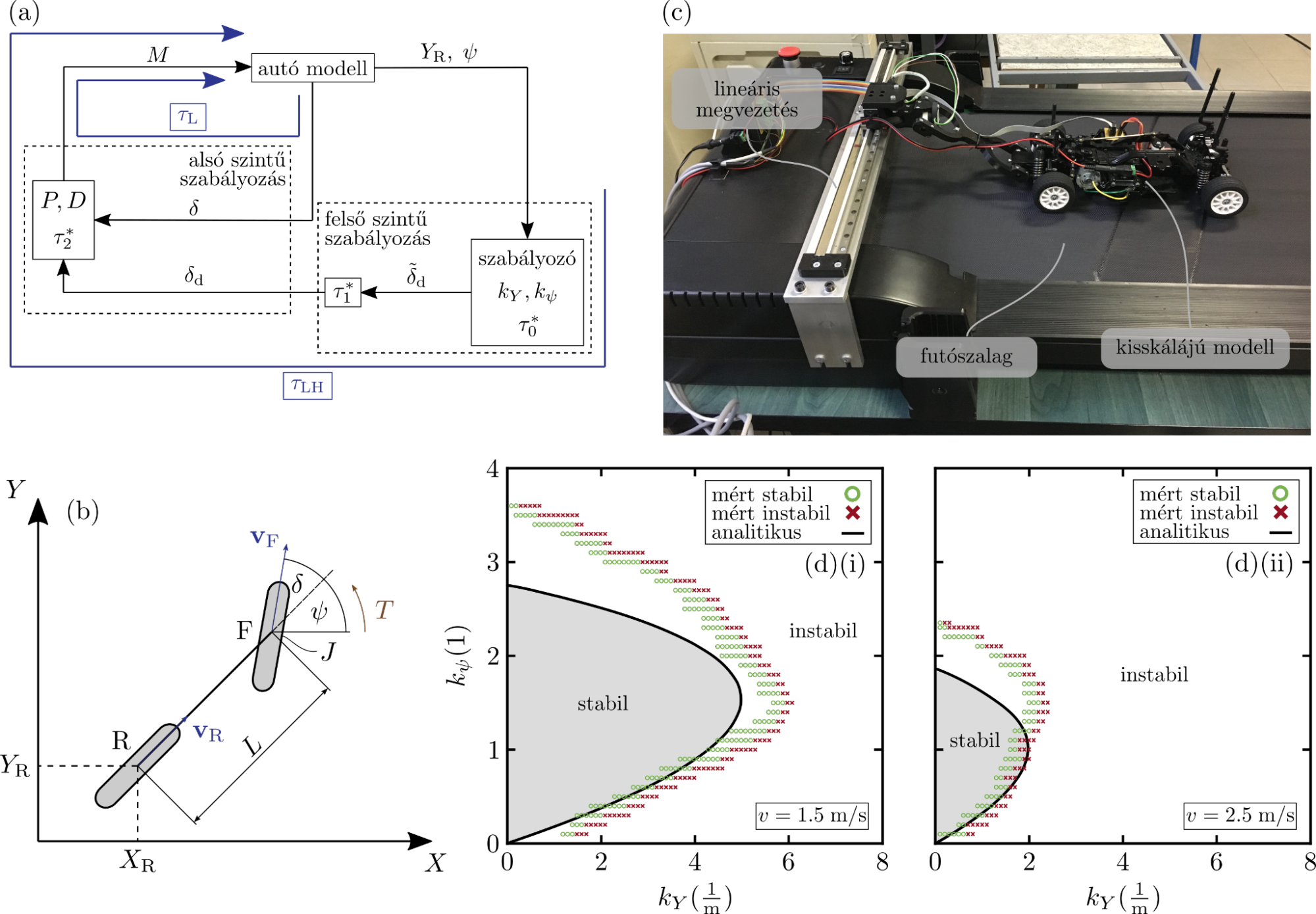
2. ábra: (a) hierarchikus kormányszabályozás. (b) autó biciklimodellje. (c) mérési összeállítás. (d) numerikus szimuláció és mérések stabilitása

 

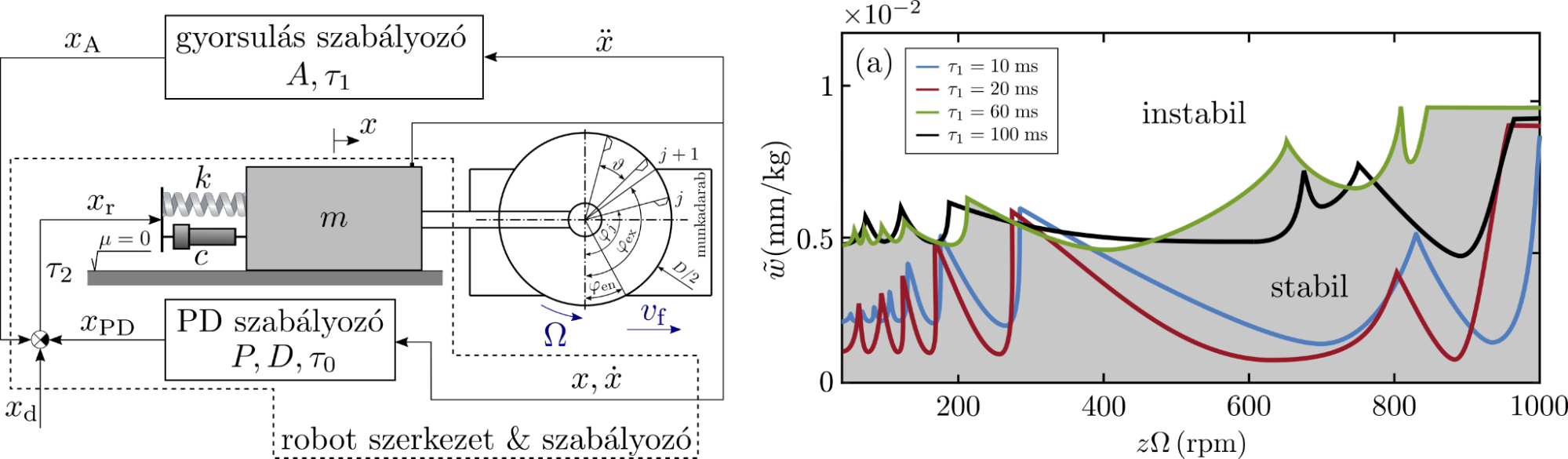
3. ábra: (a) robotszerkezet marással és gyorsulás-visszacsatolású szabályozással. (b) stabilitás különböző mintavételezési időkésésekre

 

Időben változó paraméterű rendszerek véges idejű stabilitásának analitikus közelítése

Időben változó paraméterű robotok véges idejű stabilitásának közelítéséhez egy keretrendszer megalkotása szükséges nemautonóm dinamikai rendszerekre. Célszerű ehhez a legegyszerűbb dinamikai stabilitásvesztésének vizsgálatával kezdeni. A homogén megoldás közelíthető a WKB-módszer [H7] segítségével, ha a paraméterek időben lassan változnak. A partikuláris megoldás közelítésére új, iteratív parciális integrálásra épülő (IBP) módszert [K1, F5] alkalmaztunk. Ez számos más mérnöki problémára adhat közelítő eredményt. A módszert aszimptotikus sorfejtéssel ellenőriztem, amely erre a specifikus rendszerre használható. Ahogy az a 4(i) ábrán látható a jelen numerikus módszerek nem alkalmasak véges idejű stabilitás pontos számítására, mivel ezek jelentősen eltérnek az analitikus eredménytől nagy paramétertartományon.

 

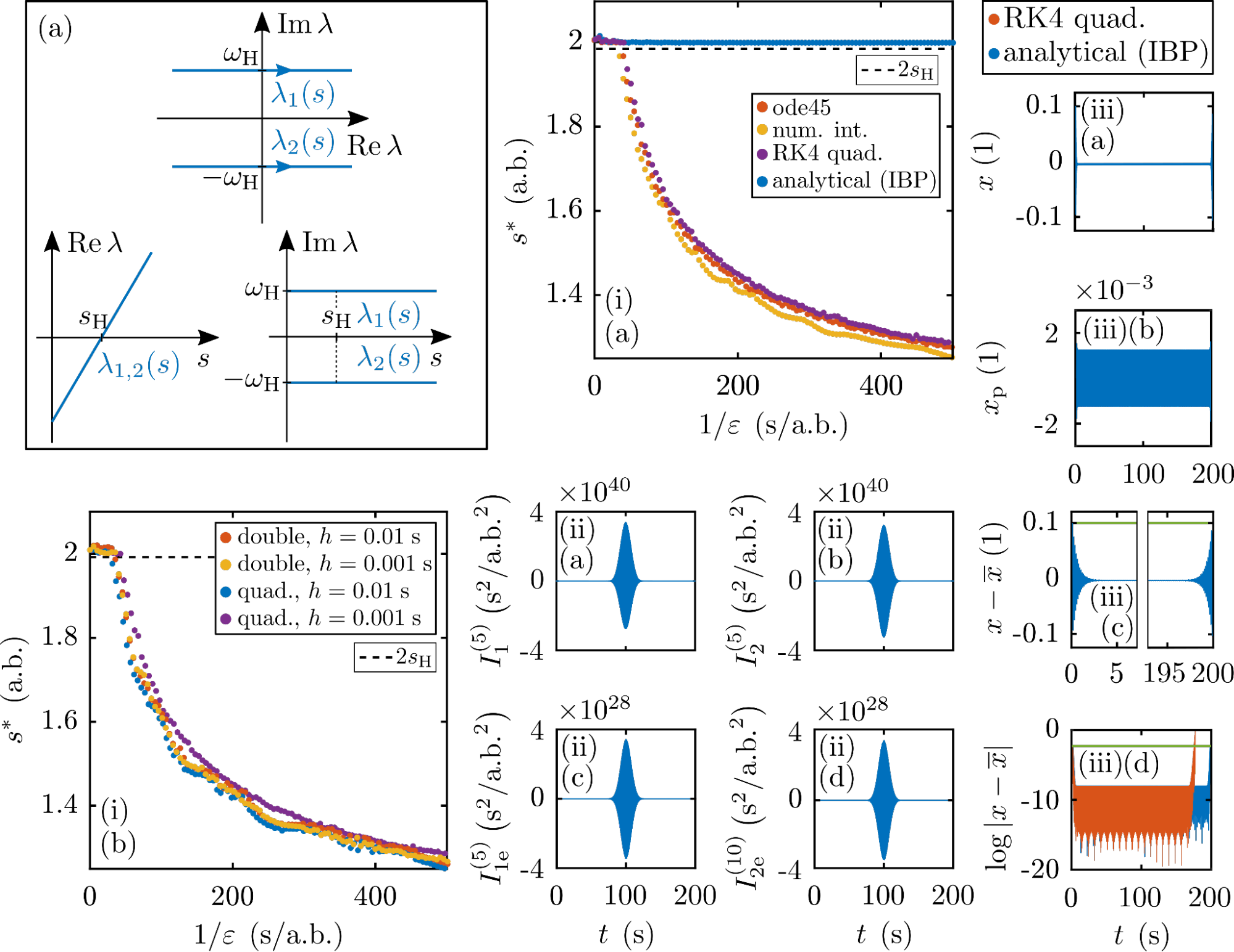
4. ábra: (a) dinamikus stabilitásvesztés sajátértékei. (i) véges idejű stabilitás analitikus és numerikus módszerekkel. (ii) partikuláris megoldás integráljának közelítése és hibája. (iii) időbeli szimulációk

Várható impakt, további kutatás

Ha a robotokkal történő megmunkálások jelen pillanatban fennálló problémái megoldhatók, akkor számos feladat alól felszabadíthatják a szerszámgépeket, megspórolva ezzel gépidőt, és előállítási költséget, ezáltal megvalósítható alternatíva lenne számos ipari alkalmazásban.

A kutatás már meglévő eredményei nemcsak fontos előrelépést jelentenek a robotokkal való megmunkálás terén, de számos más mérnöki probléma esetén is általánosan használható módszereket nyújtanak. A jövőbeli kutatás magában foglalja egy numerikus séma megalkotását, amely alkalmas nemlineáris késleltetett időben változó paraméterű rendszerek szimulálására.

Saját publikációk, hivatkozások, linkgyűjtemény.

Kapcsolódó saját publikációk listája.

Folyóirat cikkek.

[F1] Habib G., Bártfai A., Barrios A., Dombóvári Z. Bistability and delayed acceleration feedback control analytical study of collocated and non-collocated cases. Nonlinear Dynamics, 108, 2075–2096, 2022. (IF: 5,741)

[F2] Bartfai A., Dombovari Z., Hopf Bifurcation Calculation in Neutral Delay Differential Equations: Nonlinear Robotic Arms Subject to Delayed Acceleration Feedback Control. International Journal of Non-Linear Mechanics, 147, 2022. (IF: 2,985)

[F3] Bartfai A., Vörös I., Takacs D., Stability analysis of a digital hierarchical steering controller of autonomous vehicles with multiple time delays. Journal of Vibration and Control, OnlineFirst, 2023 (IF: 2,633)

[F4] Bartfai A., Barrios A., Dombovari Z., Stability Analysis of a One Degree-of-Freedom Robot Model with Sampled Digital Acceleration Feedback Controller in Turning and milling. Journal of Computational and Nonlinear Dynamics, 18(8), 2023. (IF: 1,872)

[F5] Bartfai A., Kuske R., Hogan J., Dombovari Z., Framework for the analytical approximation of finite time stability of excited dynamical systems with time-varying parameters. SIAM Journal on Applied Mathematics, 2023 (under submission, IF: 2,148)

 

Konferencia cikkek / Könyvfejezetek

[K1] Bartfai A., Kuske, R., Dombovari, Z., On the finite-time stability of dynamic stability loss in a single degree of freedom system. In Proceedings of the ISMA2022 International Conference on Noise and Vibration Engineering, Leuven, 2565–2576, 2022.

[K2] Bartfai A., Barrios, A., Dombovari, Z., Stability Analysis of a One Degree-of-Freedom Robot Model with Sampled Digital Acceleration Feedback Controller in Turning. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (ASME IDETC-CIE2022), St. Louis, 1–8, 2022.

[K3] Bartfai A., Dombovari Z., Demonstration of optimal tuning measurement of the tunable clamping table with a polymer workpiece. 38th Danubia Adria Symposium on Advances in Experimental Mechanics, 2022, no. 3125.

[K4] Bartfai A., Dombovari Z., Bistability in nonlinear elastic robotic arms subject to delayed feedback control. 10th European Nonlinear Dynamics Conference (ENOC 2022), Lyon, 1113–1114, 2022.

[K5] Bartfai A., Barrios A., Dombovari Z., Robotic Machining Applications: Delayed Acceleration Feedback Control in Milling. Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (ASME IDETC-CIE2021), online, 2021, no. 73909.

[K6] Bártfai A., Dombóvári Z., A Case Study on the Stabilization of Advanced Delay Differential Equations with Digital Controllers. 15th IFAC Workshop on Time Delay Systems (TDS2021), online, pp. 234–235, 2021.

[K7] Bártfai A., Vörös I., Takács D., Időkésés és mintavételezés hatása egy autó sávtartó szabályozásában. XXIX. Nemzetközi Gépészeti Konferencia, Kolozsvár, Románia (OGÉT 2021), 204–207, 2021.

[K8] Iklodi Zs., Gabos Z., Bartfai A., Dombovari Z., Time Domain simulation of surface topography in broaching considering tools with general cutting-edge geometries and three DoF parametric dynamics. Manufacturing Engineering Society International Conference (MESIC 2023), Sevilla, Spanyolország 2023 (elfogadott cikk)

[K9] Bartfai A., Dombovari Z., Demonstration of finite time stability in hardware-in-the-loop turning process with time-varying parameters. 39th Danubia Adria Symposium on Advances in Experimental Mechanics, Siófok, Hungary 2023 (elfogadott cikk)

[K10] Bartfai A., Dombovari Z., Időben változó paraméterű esztergálás véges idejű stabilitás vizsgálatának numerikus szimuláció problémája. XIV. Magyar Mechanikai Konferencia, Miskolc, Hungary 2023 (elfogadott cikk)

 

Linkgyűjtemény

Műszaki Mechanikai Tanszék

MTA-BME Lendület Szerszámgéprezgések Kutatócsoport

 

Hivatkozások listája

[H1] de Luca A., Farina R., Lucibello P., On the control of robots with visco-elastic joints. In: Proceedings. 2005 IEEE International Conference on Robotics and Automation, 4297–4302, 2005

[H2] Munoa J., Beudaert X., Dombovari Z., Altintas Y., Budak E., Brecher C., Stepan G., Chatter suppression techniques in metal cutting. CIRP Annals 65(2), 785–808, 2016.

[H3] Hazarika S.M., Dixit U.S., Robotics: history, trends, and future directions, chap. 7. Materials Forming, Machining and Tribology. Springer International Publishing, 213–239, 2018.

[H4] Insperger T., Stepan G. and Turi J., Delayed feedback of sampled higher derivatives. Philosophical Transactions of the Royal Society A 368(1911): 469–482, 2010.

[H5] Barton D.A. Krauskopf B., Wilson R.E., Collocation schemes for periodic solutions of neutral delay differential equations. Journal of Difference Equations and Applications, 12(11), 1087–1101, 2006.

[H6] Insperger T., Semi-Discretization for Time-Delay Systems. Springer-Verlag New York: Stability and Engineering Applications, 2011.

[H7] Baer S.M., Erneux T., Rinzel J., The slow passage through a Hopf bifurcation: Delay, memory effects, and resonance. SIAM Journal on Applied Mathematics, 49(1), 55–71, 1989.