Villamosmérnöki Tudományok  Doktori Iskola 

BME-VIK, Villamos Energetika Tanszék

Témavezető: Dr. Hartmann Bálint

Regionális fotovillamos termelés-előrejelzési modell kidolgozása

A kutatási téma néhány soros bemutatása

Az európai energetikai dekarbonizációs célok elérése érdekében az elmúlt évtizedben a fotovillamos energiatermelés dinamikus térnyerése volt megfigyelhető. A technológia időjárásfüggő, volatilis termelői viselkedése azonban számos kihívást generál a hálózat üzemeltetői számára. Jelen kutatás célja a valós idejű méréssel nem rendelkező kisméretű napelemes egységek termelésének előrejelzése regionális szinten.

 

A kutatóhely rövid bemutatása

 

A Dr. Hartmann Bálint által vezetett MTA-BME FASTER Lendület Kutatócsoport célja a kiterjedt, alacsony műszerezettségű kisfeszültségű villamosenergia-hálózat megfigyelhetőségének növelése. A kutatási tevékenység fókuszában olyan algoritmusok, eljárások fejlesztése áll, melyek érdemben képesek feltárni a hálózaton fellépő rendkívüli eseményeket (pl.: lokális kieséseket), növelik a hálózati üzemvitel flexibilitását, valamint felkészítik azt a megjelenő diszruptív technológiák (pl.: e-mobilitás) befogadására.

 

A kutatás történetének, tágabb kontextusának bemutatása

 

A fotovillamos energiatermelés hazai és nemzetközi részaránya napjainkban dinamikus emelkedést követ. A telepítésre kerülő kis egységteljesítményű, jellemzően háztetőkön, közületeken elhelyezett termelők a kisfeszültségű elosztóhálózatra csatlakoznak földrajzi koncentráció nélkül. 2021 végére a háztartási méretű kiserőművek száma elérte a 90 000 darabot, névleges beépített teljesítményük pedig az 1400 MWp teljesítményt. A hazai mintegy 4,1 millió háztartást körülbelül 60–65 ezer darab közép/kisfeszültségű transzformátorkörzet látja el, a rendszer hatalmas kiterjedéséből adódóan annak műszerezettsége rendkívül alacsony. A valós idejű mérési információk hiánya ezidáig a kiszámítható, statisztikai módszerekkel jól becsülhető fogyasztás mellett nem okozott problémát.

A háztartási méretű kiserőművek megjelenésének hatására azonban a lehetséges rendszerállapotok száma növekszik, azaz a lokális feszültségviszonyok és a teljesítmény-áramlások iránya már nem állapítható meg ennyire egyszerűen. A napelemes termelés egyrészt megnehezíti az optimális üzemvitel fenntartását, valamint a teljesítményáramlás megfordulása mellett a szabványos tartományt meghaladó mértékben emelheti a feszültség értékét. A probléma megoldása érdekében a jelenlegi passzív hálózatüzemeltetést egy aktív beavatkozáson alapuló megközelítésnek kell felváltania. Ennek kulcsa nemcsak a valós idejű mérés, hanem a lokális, időjárásfüggő energiatermelés minél pontosabb előrejelzése. Tekintettel arra, hogy az említett háztartási méretű kiserőművek szintén nem rendelkeznek idősoros (rendszeres távleolvasást biztosító) mérővel, az általuk generált termelés modellezése a hazai hálózati viszonyok ismeretében különösen égető feladat.

 

A kutatás célja, a megválaszolandó kérdések

 

A napelemek termelését a környezeti paraméterek változása, ezen belül elsősorban a globálsugárzás értéke befolyásolja. Ennek napon belüli alakulását egyrészt a Nap és a Föld pozíciója, másrészt a légköri változások (döntően a felhőátvonulások) határozzák meg. Míg az előbbi pontosan modellezhető, utóbbi sztochasztikus viselkedéssel rendelkezik.

 

 

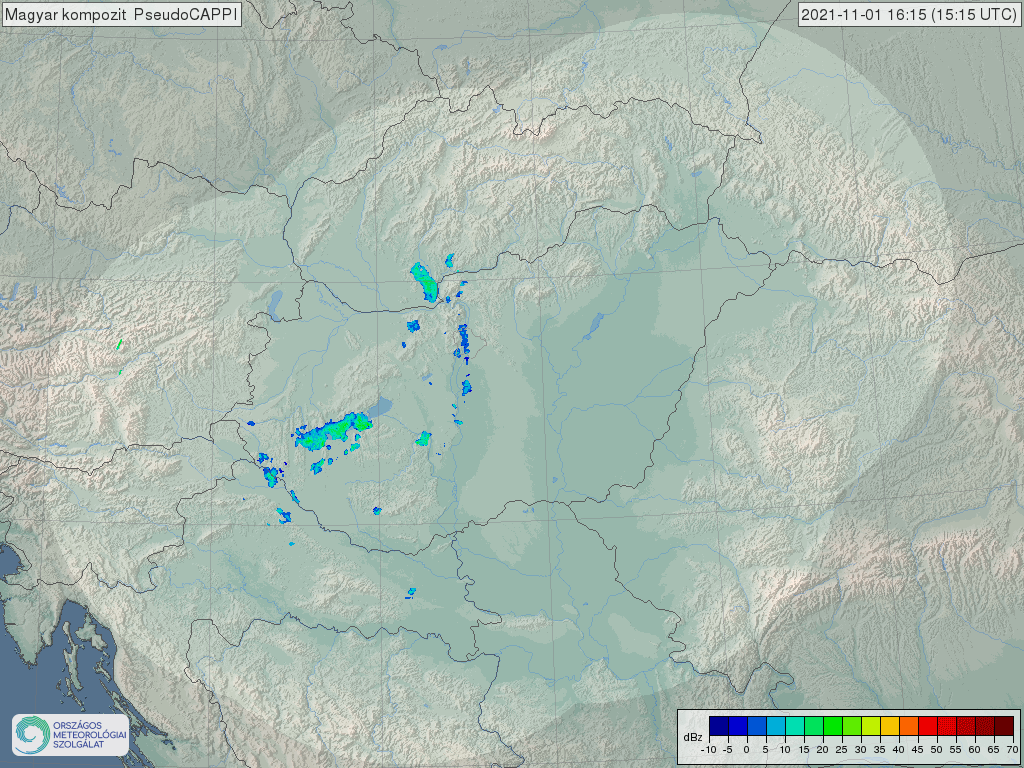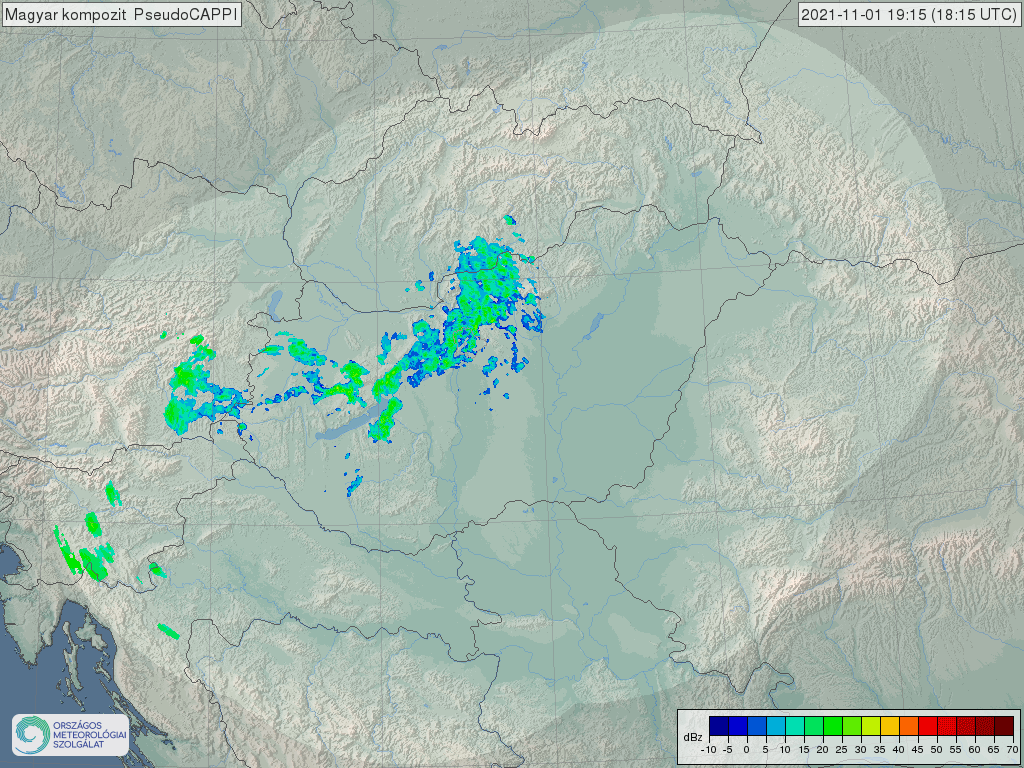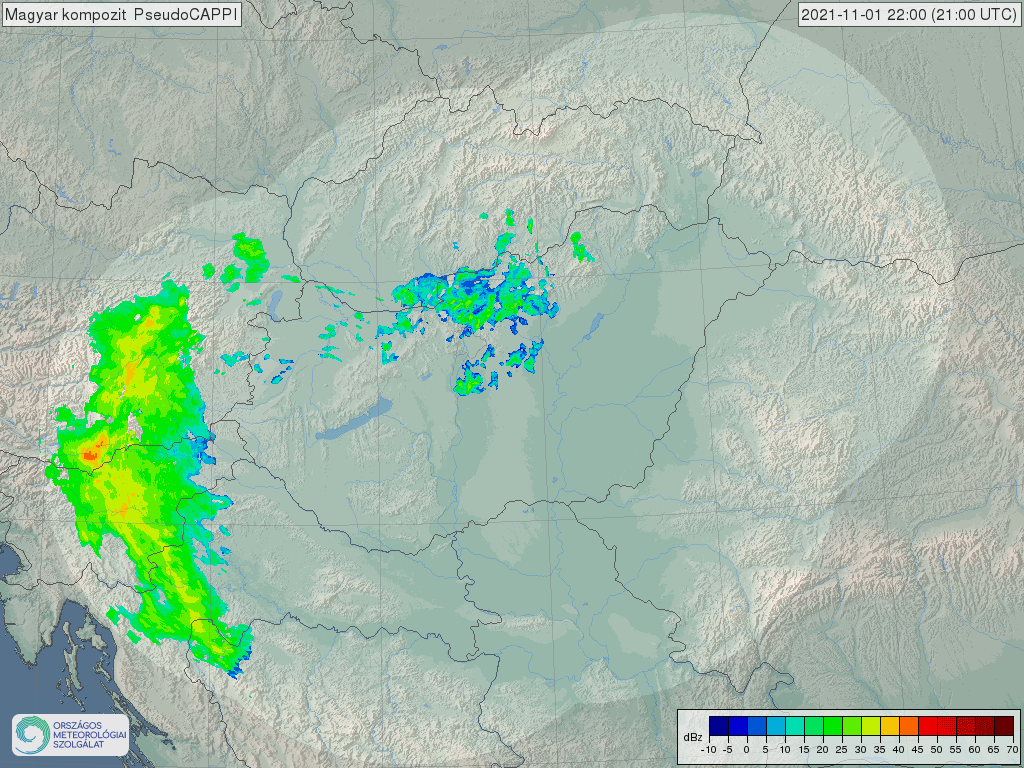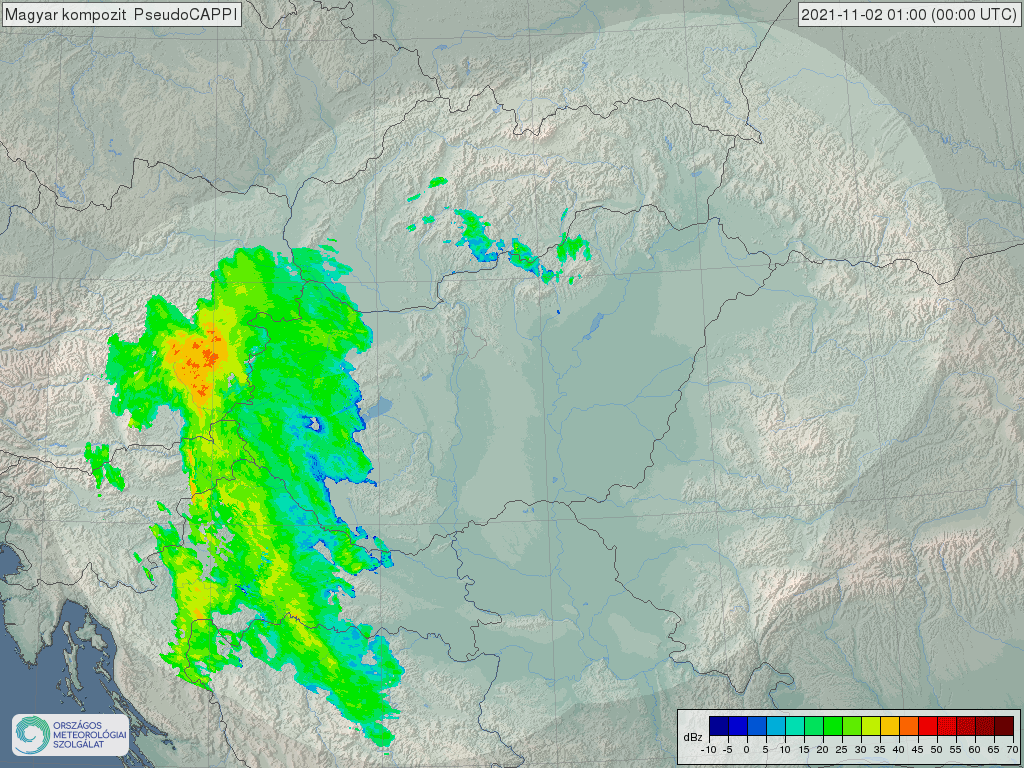
1. ábra: OMSZ kompozit radarkép 2021 november 1-én

 

A napelemes termelés időjárásfüggő jellegéből adódóan egy nagy pontosságú, napon belüli termelés változásokat leíró előrejelző modell létrehozásának nehézsége két okra vezethető vissza:

1) a termelés gyors, volatilis időbeli változásaira és

2) a folyamatot befolyásoló környezeti globálsugárzás térbeli lokalitására.

A pontos lokális termelés-előrejelzés egyik kulcsa tehát a minél nagyobb térbeli-időbeli felbontás elérése.

 

A kutatás célja a fotovillamos energiatermelés változását erős korreláció mellett leíró globálsugárzási paraméter időbeli-térbeli összefüggéseinek feltárása geostatisztikai módszerek segítségével. Ennek keretében az alábbi kérdésekre kerestem a választ:

●     Milyen predikciós megközelítés képes a lehető legnagyobb pontossággal lokális becslést adni?

●     Milyen statisztikai kapcsolat van két, adott távolságra található globálsugárzás- mérőpont adatai között? Vannak karakterisztikusan eltérő naptípusok (pl. tiszta ég vs. felhős nap)?

●     A felhőátvonulások sebességére, valamint két mérési pont közötti korrelációra milyen hatással van a szél iránya és sebessége?

●     Mi az a kritikus legkisebb térbeli távolság, amelyen belül még érdemes egy mérőállomás adatait felhasználni a becsléshez? Több állomás adatát milyen módszerrel érdemes együttesen figyelembe venni?

 

 

Módszerek

 

A napjainkban széles körben alkalmazott, historikus adatokon alapuló időjárásfüggő termelésbecslő eljárások (pl.: neurális hálózatok, idősoros, statisztikai modellek) alkalmazásának fő korlátja, hogy nem tudjuk leírni a gyors, napi léptékű trendekbe nem illeszkedő termelésváltozásokat. Ezen gyors események időbeli dinamikájának leírásához az ezt befolyásoló környezeti paraméterek (pl.: felhőátvonulás, globálsugárzás) mérésére, modellezésére van szükség. Az ehhez kifejlesztett becslési modellek (pl.: égboltkamerák) adatai jellemzően csak egy szűk földrajzi tartományban hasznosíthatók.

A földi légkör változásait leíró, nagy számítási igényű numerikus időjárás modellek (pl.: WRF, AROME) képesek a környezeti paraméterek nagy pontosságú és területileg átfogó becslésére, térbeli granularitásuk azonban néhány km², illetve időben jellemzően órás felbontású becslést biztosítanak.

Tekintettel arra, hogy a fotovillamos termelést erős korrelációs kapcsolattal leíró globálsugárzás – szemben például a hőmérséklettel – területileg koncentrált paraméter, szükség van a térbeli-időbeli függőségek feltárására. Ezen aspektus jelentősége az említett aktív hálózati üzemvitel szempontjából még inkább felértékelődik, ugyanis nem csak egy helyszínre kell pontos becslést adni, hanem egy régió minden egyes termelője számára. Azaz olyan megoldásra van szükség, mely lényegesen nagyobb térbeli (és időbeli) felbontással rendelkezik.

A fentiek fényében a kutatásom során egy numerikus globálsugárzás-előrejelző modell által generált adatsor időbeli-térbeli felbontásának növelését tűztem ki célul. Ehhez első lépésként historikus globálsugárzás-mérési adatokból statisztikai összefüggések alapján klasztereztem az egyes naptípusokat felhőzöttség alapján (felhős, részben felhős, tiszta ég). Ezt követően megállapítottam a részben felhős napok esetében, hogy a földrajzi távolság függvényében miként változik két állomás közötti korreláció az idő függvényében a jellemző szélirány esetén. Ez a lépés azon a feltételezésen alapult, hogy az átvonuló felhők a földrajzi távolsággal arányos időbeli késleltetéssel jelennek meg két mérési adatban. Az eredményeket Hovmöller-diagramon ábrázoltam.

A kapott valószínűségi összefüggések alapján megállapítottam, hogy mekkora az a kritikus földrajzi távolság, amelyen belül érdemes egy mérési adat eredményeit felhasználni. Az eredmények alapján létrehoztam egy modellt, mely krigeléssel képes tetszőleges földrajzi pontban a környező mérési adatok alapján meghatározni a várható globálsugárzás értékét. A krigelés a közeli mérési adatok egy olyan lineáris kombinációját határozza meg, ahol a lineáris kombináció súlyai függenek a mérési helyek egymáshoz viszonyított pozíciójától és közvetve a mérések értékétől is. Az így kapott krigelési modellt használtam fel nem a múltbeli, hanem immáron az előrejelzési adatok tetszőleges földrajzi pontra történő pontosításához.

 

 

Eddigi eredmények

 

A kutatáshoz mind historikus, mind előrejelzésből származó adatot felhasználtam. Az előrejelzés térbeli-időbeli felbontásának pontosítása érdekében az Országos Meteorológiai Szolgálat globálsugárzás-méréseit vizsgáltam Pest megyében (ld. 2. ábra).

 

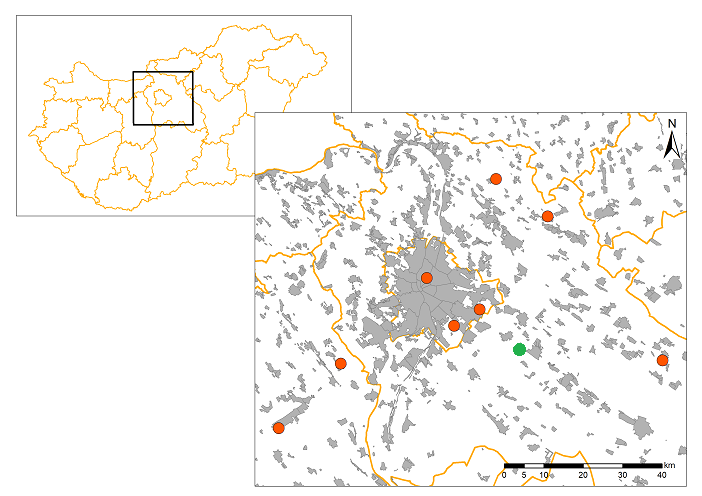
2. ábra: Kutatás során felhasznált OMSZ-mérőállomások helyzete (piros) és a validációhoz használt egyik háztartási méretű fotovillamos termelő földrajzi pozíciója (zöld)

 

A kutatás során az alábbi 3 fő lépés segítségével hoztam létre a termelés becslésemet:

 

1.     Az egyes mérőállomások adatai közötti azonosítható időbeli késleltetés feltárása a távolság függvényében

 

A rendelkezésre álló, nyolc Pest-megyei mérési ponton rögzített adat között időben bizonyos késleltetés és szignifikancia mellett kölcsönös kapcsolat áll fenn. Adott szélirány esetén két, egy vonalban található mérőállomás mérési adatai között a korrelációs kapcsolatot a felhőátvonulás sebessége adhatja meg. A cél ezen kapcsolat „erősségének” meghatározása a távolság függvényében, ami Hovmöller-diagram segítségével került kiértékelésre. Mindenekelőtt az egyes napok 3 klaszterbe kerültek felosztásra: tiszta ég, részben felhős, felhős napok. A Hovmöller-diagram alapján jól láthatóak a különbségek. Minden esetben egy 3 dimenziós sűrűségfüggvényt láthatunk “felülről”, ahol az y tengely a két mérőállomás közötti késleltetés idejét, míg az x tengely a közöttük lévő távolságot ábrázolja. Tehát két állomás esetében, ahol a köztes távolság 40 km, minden esetben az x tengely 40 km-es értékénél találjuk a köztük található eloszlás alakulását a késleltetési idő függvényében. Megfigyelhető, hogy a „tiszta ég” napok esetében a késleltetési idő a távolságtól függetlenül 0 perc körül koncentrálódik, annak köszönhetően, hogy ilyenkor nincs érdemi eltérés a rögzített mérési adatok között (nincs légköri „zavaró” tényező). A részben felhős esetet vizsgálva azonban már lényegesen nagyobb az eloszlás szórása (jobban “elterül” az eloszlásgörbe).

 

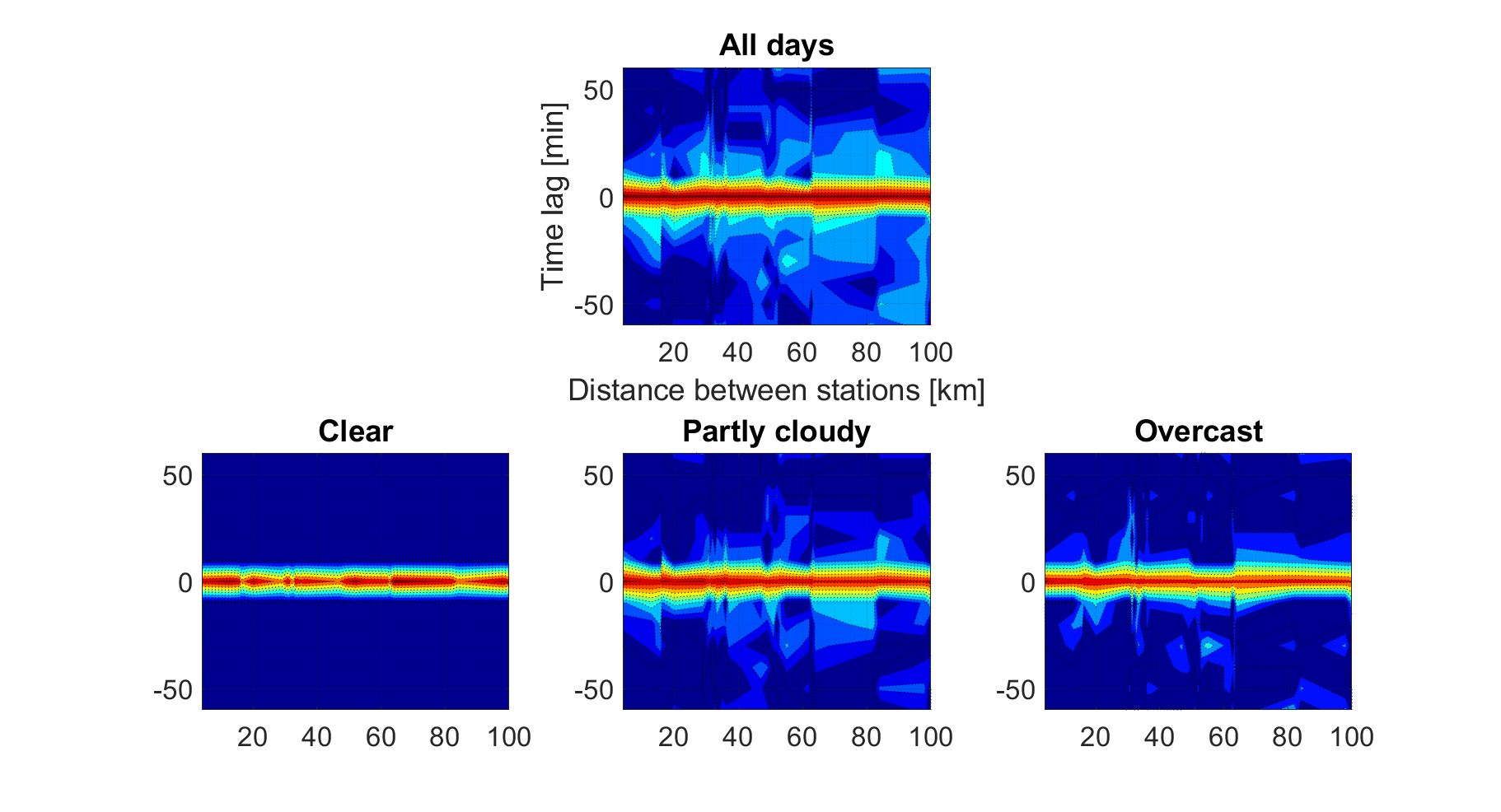
3. ábra: Hovmöller-diagramok eltérő felhőborítású napok esetében (tiszta ég, részben felhős, borult – alsó sor balról jobbra), illetve a teljes adatsorra vetítve (fent középen)

 

2. Kritikus földrajzi távolság meghatározása

 

Ugyan a Hovmöller-diagram szemléletes képet ad az állomás mérési adatok közötti összefüggésekről. Egy adott földrajzi ponton található napelem becsléséhez azonban nem szükséges az összes mérési adatot felhasználni. Ezért a második lépés célja egy kritikus földrajzi sugár meghatározása, amelyen belül található mérési pontok felhasználása a historikus adatok alapján elég erős korrelációjú az eredményes felhasználáshoz. Tehát lényegében a Hovmöller-diagramon látható eloszlások szórása látható a 4. ábrán minden mérőállomás-párosítás mellett.

 

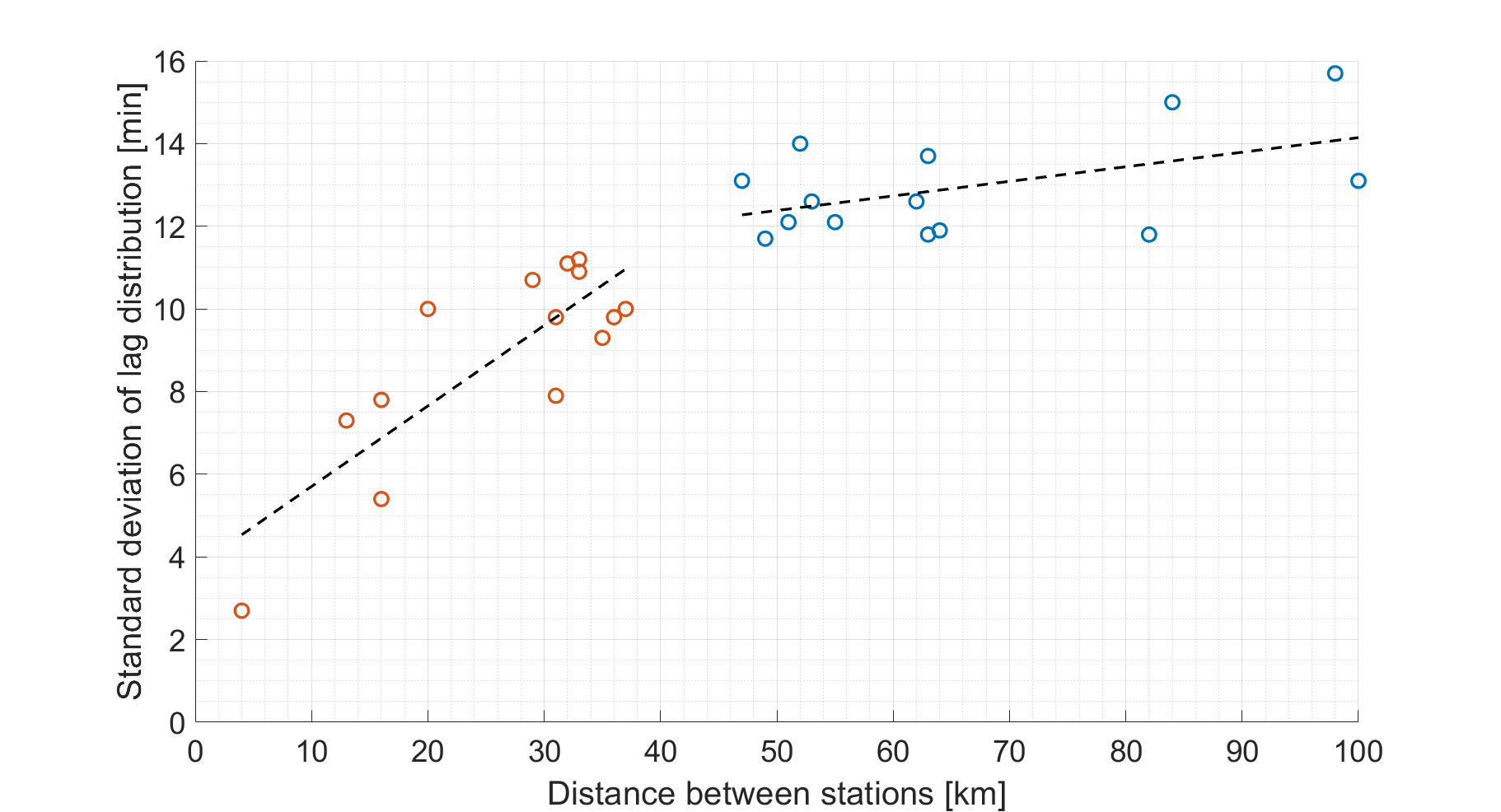
4. ábra: Mérőállomás-páronként az időbeli késleltetés eloszlásgörbéje szórásának változása

 

A 4. ábra már egyértelmű bizonyítéka annak, hogy a mérőállomás-távolságok függvényében egyértelmű törés látható a szórások nagyságában. Ez alapján minden napelemes termelő körül egy 20 km sugarú körben található adatok kerülnek csak felhasználásra.

 

3. Kapcsolat a múlt és a jövő között - a historikus adatok eredményeinek felhasználása az előrejelzések térbeli-időbeli felbontásának növeléséhez

 

A korábbi lépések során kapott statisztikai összefüggések segítségével a numerikus előrejelzés által előállított globálsugárzás-becslés került pontosításra. Az előrejelző modell egy raszterháló sarokpontjaiban határoz meg értékeket (piros pontok), míg a vizsgált termelő a zöld pontban helyezkedik el az 5. ábrán. Erre a földrajzi pontra krigelés segítségével kerül meghatározásra a várható globálsugárzás nagysága a közeli, 20km-es körzetben található becslési értékek lineáris kombinációjával. Ez a globálsugárzás érték végül egy virtuális napelemmodell segítségével lesz valós termeléssé átszámítva.

 

 

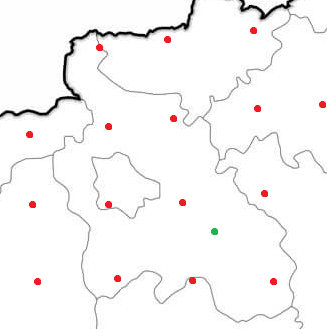
5. ábra: Numerikus időjárási modell eredményeinek (piros) és a validációhoz használt egyik fotovillamos termelő helyzetének szemléltetése

 

A bemutatott modell eredményeit egy konkrét napelemes kiserőmű 2 hónapos termelési adataival validáltam. A bemutatott modell egyszerre képes a rendkívüli felhőátvonulások hatásait is figyelembe venni (erre a legtöbb becslő információ hiányában képtelen), valamint a krigelés segítségével tetszőleges földrajzi pontra adható becslésre, azaz regionális szintű becslésre is alkalmas. Az eddigi futtatási eredmények alapján a modell pontossága jelentősen meghaladja a referencia előrejelző modellek (Neurális hálózat, ARIMA és perzisztencia-modell) pontosságát.

 

 

Várható impakt, további kutatás

 

A kidolgozott modell újdonsága annak flexibilis felhasználhatóságából adódik. Az irodalomban megjelenő termelésbecslő modelleket jellemzően néhány földrajzi pont adatai alapján szokás validálni. Esetünkben ez a régióban rendelkezésre álló további termelőre is megtörtént. További cél az eredmények kiterjesztése országos szinten, valamint az idősoros (valós idejű) méréssel nem rendelkező háztartási méretű napelemes termelés előrejelzése regionálisan. Az eredmények segítségével mérési adat nélkül is lehetőség nyílik a kritikus kisfeszültségű hálózatrészek modellezésére, emellett alternatívát lehet teremteni a szükséges, de rendkívül költséges hálózati felműszerezésnek, és ezzel elősegíteni a megújuló energiaforrások hálózatba integrálási folyamatát.

Az eredményeket összefoglaló cikk egy impaktfaktoros folyóiratba került benyújtásra, továbbá közérthető formában is ismertettem az MTA Magyar Tudomány Ünnepe és szélesebb szakma által közismert MEE Vándorgyűlés alkalmából, valamint az Élet és Tudomány hasábjain.

 

 

 

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája

 

Kapcsolódó folyóirat publikációk

 

B. Sinkovics: A napelemek termelésének előrejelzése a múlt és a jelen tükrében, Élet és Tudomány, 25, (2022)

I. Táczi, B. Sinkovics, I. Vokony, B. Hartmann: The Challenges of Low Voltage Distribution System State Estimation – An Application Oriented Review. Energies (2021), 14, 5363

B. Sinkovics, J. Kiss, B. Polgári, J. Csatár: Co‐simulation framework for calculating balancing energy needs of a microgrid with renewable energy penetration, International Journal of Energy Research, pp. 18631–18643, vol. 45 (2021)

B. Sinkovics, B. Hartmann: Analysing Effect of Solar Photovoltaic Production on Load Curves and their Forecasting, Renewable Energy and Power Quality Journal, pp. 760–765. , 6 p. (2018)

B. Sinkovics, I. Táczi, I. Vokony, B. Hartmann: A novel adaptive day-ahead load forecast method, incorporating non-metered distributed generation: a comparison of selected European countries, Mathematical Modelling of Contemporary Electricity Markets (MMCEM), pp. 62–81, Chapter 3, Elsevier (2020)

 B. Hartmann, A. Kazsoki, V. Sugár, B. Sinkovics: Napsugárzás-mintázat kategorizálási módszereinek kritikai szemléletű összehasonlítása, Magyar Energetika pp. 18–24., (2020)

B. Sinkovics: Fogyasztás és termelés egyensúlya: A jövő megoldása az energiaéhségre? Élet és Tudomány, pp. 233-235, (2019)

 

 

Kapcsolódó konferencia előadások

B. Sinkovics: Fotovillamos termelésbecslő modell bemutatása térbeli-időbeli krigelés alkalmazásával, MEE Vándorgyűlés (2021)

I. Táczi, B. Sinkovics, I. Vokony, B. Hartmann: Conceptual Analysis of Distribution System State Estimation of Low Voltage Networks, International Conference on Renewable Energy and Power Quality (ICREPQ 2020)

B. Sinkovics: Computer-Based Algorithm to Predict the Change in Daily Electricity Demand, Advanced ICT Tools and Methods for Cyber-Physical Systems and Biomedical Applications, Esztergom, Hungary (2019)

B. Sinkovics, B. Hartmann: Analysing Effect of Solar Photovoltaic Production on Load Curves and their Forecasting, International Conference on Renewable Energy and Power Quality: ICREPQ'18 Vigo, Spain: Europe-an Association for the Development of Renewable Energies, Environment and Power Quality (EA4EPQ), pp. 1–6. (2018)

 

Linkgyűjtemény

https://hartmannbalint.wixsite.com/faster

 

 

Hivatkozások listája

 

D. Yang, Z. Dong, T. Reindl, P. Jirutitijaroen, W. M. Walsh, Solar irradiance forecasting using spatio-temporal empirical kriging and vector autoregressive models with parameter shrinkage, Solar Energy, vol. 103, pp. 550­–562, 2014

D. Yang, Z. Dong, A. Nobre, Y. S. Khoo, P. Jirutitijaroen, W. M. Walsh, Evaluation of transposition and decomposition models for converting global solar irradiance from tilted surface to horizontal in tropical regions, Solar Energy, vol. 97, pp. 369–387, 2013