Kandó Kálmán Doktori Iskola  

BME Közlekedés- és Járműmérnöki Kar, Gépjárműtechnológia Tanszék

Témavezető: Dr. Török Árpád

Autonóm közlekedési rendszerek helyváltoztatási folyamatainak optimalizálása

A kutatási téma néhány soros bemutatása

A járműtechnológiai fejlesztések jelenlegi irányai a jövő közlekedési rendszerének változását vetítik előre. Az autonóm járművek várható elterjedése megteremti a közlekedési rendszer hatékonyabb befolyásolásának lehetőségét. A közlekedési folyamatokhoz kapcsolódó veszteségek csökkenthetővé, a forgalom várhatóan biztonságosabbá válik, melyekhez kapcsolódóan számos kutatási feladat vált és válik szükségessé. Munkám során arra kerestem a választ, hogyan jellemezhető és javítható a forgalmi áramlatok lebonyolódása és biztonsága olyan környezetben, amelyben kizárólag önvezető járművek közlekednek. A kooperatív járműirányítás és a dinamikus forgalommenedzsment céljait és eszköztárát egyesítve időben és térben diszkretizált, bináris változójú optimalizációs modellt dolgoztam ki. A biztonságot jellemző indikátorokat és a környezet leképezési struktúráinak releváns paraméterekre gyakorolt hatását a kidolgozott modell segítségével határoztam meg.

 

A kutatóhely rövid bemutatása

A kutatómunkát a BME KJK Gépjárműtechnológia Tanszékén végzem, a Dr. Török Árpád által vezetett Automotive Safety and Security kutatócsoport keretein belül. A kutatócsoport célja a járműfejlesztési folyamatokhoz kapcsolódó biztonsági és kiberbiztonsági szempontok integrált matematikai modellezése és ez alapján a magasan automatizált járműrendszerekhez kapcsolódó biztonsági kockázatok minimalizálása. A tanszék szorosan együttműködik a kutatási terület vezető ipari szereplőivel, kutatóhelyeivel.

 

A kutatás történetének, tágabb kontextusának bemutatása

A magasan automatizált járművek terjedésével a közlekedési rendszer hatékonyságának további javítására nyílik lehetőség [1], [2]. Ugyanakkor a rendszer elemeinek nagy száma a kapcsolódó optimalizálási problémák komplexitását jelentős mértékben megnöveli [3]. Jelenleg még nem tisztázott, milyen irányelvek mentén (egyéni közlekedés/megosztott, központosított rendszerek) fejlődik tovább a jövő közlekedési rendszerének forgalmi menedzsment koncepciója [4], [5]. A kutatások egy része az egyéni járművek döntési problémáinak kezelésére [6], más része hálózati szintű megoldások kialakítására fókuszál. Ez utóbbi megközelítések szerint, amennyiben a járművek pozícióját, mozgását a központi menedzsment rendszer befolyásolja, jobban megközelíthetjük a rendszerszintű optimum állapotát [7].

Az autonóm közlekedési rendszerekkel kapcsolatos biztonsági elvárások fontosságát számos tanulmány hangsúlyozza [8], [9]. Bármely irányba fejlődik tovább a jövő közlekedési rendszere, a közlekedési tér elemeinek járművekhez rendelése egyértelmű módon kell, hogy megvalósuljon. A fenti feltétel az autonóm közlekedési rendszerek úgynevezett foglaltságiháló-alapú megközelítése révén (1. ábra) egyértelműen teljesíthető [10].

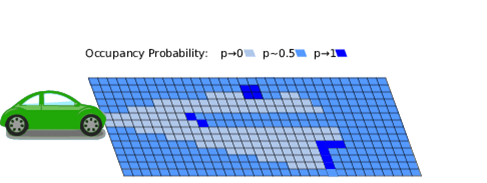
1. ábra: A foglaltságiháló-alapú leképezés szemléltetése [11]

Ugyanakkor a szakirodalomban fellelhető kutatási eredmények alapján a környezet leképezésének struktúráját, vagyis a térbeli elhelyezkedés modellezésére alkalmas hálózatok szerkezetét és szomszédsági viszonyait eddig elsősorban környezeti tényezőnek tekintették, nem pedig a közlekedési rendszer aktív elemének. A foglaltságiháló-koncepciót számos tanulmány vizsgálta [12], [13], de ezek elsődlegesen nem a leképezés struktúrájának hatékonyságra gyakorolt hatásvizsgálatára irányultak. Ezen felül megállapítható, hogy a különböző, autonóm rendszerekhez kapcsolódó forgalmi menedzsment rendszerek esetében a környezet leképezéséhez általában a négyzetrácsalapú struktúrát alkalmazzák, miközben számos egyéb struktúra is kialakítható.

 

A kutatás célja, a megválaszolandó kérdések

Az irodalomkutatás során feltárt megfontolások figyelembevételével kutatásaim elsősorban a teljesen autonóm közlekedési rendszerekre irányultak, az egyéni járművek döntéseit központilag befolyásolhatónak tekintettem. A közlekedési rendszer hatékonyságának maximalizálása céljából olyan eljárás kifejlesztésére törekedtem, mellyel lehetőség nyílik a közlekedési folyamatokhoz kapcsolódó veszteségek (pl. eljutási idő, baleseti kockázat) rendszerszintű minimalizálására. A közlekedési rendszer biztonságára vonatkozó növekvő elvárások tükrében további célom az autonóm közlekedési rendszer működését jellemző, a rendszer működési sajátosságaihoz igazodó biztonsági paraméterek kidolgozása és vizsgálata volt.

A kutatási célok eléréséhez az autonóm személyközlekedési rendszer forgalmi modellezésére alkalmas keretrendszer kialakítására volt szükségem. Vizsgálni kellett, hogy milyen módszerekkel lehet hatékonyan, akár valós időben is működő módon leképezni a forgalomszétosztás problémáját. Az útdíjrendszer, mint a forgalmi igényekre és kijelölt útvonalakra hatást gyakorló tényező modellbe építésével vizsgálat alá kívántam vonni azt is, hogy miként lehet az alapmodell működését kiterjeszteni különböző externális paraméterek befolyásoló hatásának vizsgálata érdekében.

Az alapmodelleket továbbfejlesztve cél volt a közlekedési hálózat és az idő diszkretizálása révén a forgalmi áramlatok helyett az egyéni járművek mozgásának befolyásolására alkalmas modell kidolgozása. Ezen rendszer a kooperatív járműirányítás és a dinamikus forgalom menedzsment megközelítéseit ötvözve biztosít lehetőséget a közlekedési folyamatok optimalizációjára. A helyes működés vizsgálatához a modell szoftveres leképezése, és különböző mintahálózatokon elvégzett vizsgálatok voltak szükségesek. A valós idejű forgalmi optimalizáció megvalósításához a modellt leíró egyenlet- és egyenlőtlenség rendszerek komplexitását a lehető legkisebb mértékűre kellett csökkenteni.

A kidolgozott modellel lehetőséget teremtettem az autonóm közlekedési rendszer hatékonyságának és közlekedésbiztonságának vizsgálatára. Ehhez az optimalizációs célfüggvény vizsgálatán kívül a biztonságot jellemző indikátorok kidolgozására volt szükség. Ezen felül kutatási irányként fogalmaztam meg a közlekedési hálózat leképezésének releváns paraméterekre gyakorolt hatásának vizsgálatát is.

 

Módszerek

A térben és időben diszkretizált modell keretrendszerének kialakítása során az optimalizáció egyszerűsítése, ezáltal a valós idejűség támogatása érdekében bináris, egészértékű változót képeztem (2. ábra). A modellem döntési változója (x_k,j,i) a k-adik jármű i-edik lokációban való tartózkodását írja le a j-edik időlépésben, bináris értékkészlettel.

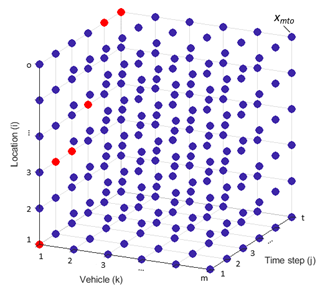
2. ábra: Az optimalizáció változója alapján képzett 3D-s mátrix
(piros kijelölés: az első jármű trajektóriája)

Tekintve, hogy a számítógépek nem tudnak végtelenül sok, folytonosan változó mennyiséget kezelni, a numerikus modellek szükségszerűen véges sok változóval közelítik meg a valóságot, illetve annak matematikai modelljét. A folytonos attribútumok kategorikus attribútumokká alakítását diszkretizálásnak nevezzük. Vizsgálataim során a forgalommenedzsment-feladatok ellátása érdekében mind a közlekedésre szolgáló tér (3. ábra), mind pedig az idő felosztása szükségessé vált:

●       a folytonos időtartományt egészértékű időpillanatokra osztottam, másodperces felbontással,

●       a közlekedési hálózatot 5 méteres átmérőjű beírható körrel jellemzett, irányított sokszögekre (lokáció) bontottam fel (egy átlagos személygépjármű méreteit figyelembe véve).

Vizsgálataim alapján a fenti felosztás nagyfokú részletességet biztosítva támogatja a hatékony forgalommenedzsmentet, miközben kezelhető mértékű komplexitást eredményez.

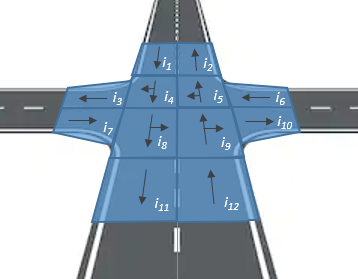
3. ábra: Egy egyszerű útkereszteződés lokációkra osztásának sematikus ábrája

A számítási komplexitás további csökkentését a valós idejűség támogatása és a minél nagyobb számú változó kezelése érdekében egyaránt fontos feladatként azonosítottam. A cél megvalósításához olyan módszereket dolgoztam ki, melyekkel a korlátozó egyenletek és egyenlőtlenségek száma úgy csökkenthető, hogy a megoldás hatékonysága és megbízhatósága nem romlik. A módszerek alapelve, hogy a korlátozásokat leíró kifejezésekben a változó figyelembe vett értékkészletét csökkentjük:

●       a sebességkorlát figyelembevételével a további vizsgálatokból kizártam az egy időlépés alatt maximális sebességgel nem beutazható lokációpárokat,

●       a gyorsulás megengedett maximális értéke alapján az első időlépésben elérhető lokációk körét szűkítettem,

●       a hálózat speciális pontjait képező forrás- és nyelőpontok azonosításával, és vizsgálatból való elhagyásával a biztonság szempontjából nem kritikus feltételeket tovább csökkentettem.

A forgalmi áramlatok biztonságát jellemző indikátorok módszertani kidolgozása során a közlekedésbiztonsági kutatások eredményeiből indultam ki. A biztonsági szempontból kritikus rendszerállapot (ütközések) fennállási kockázatának vizsgálata érdekében a keresztező járműmozgások időbeli távolságának meghatározására törekedtem. Felismerve továbbá, hogy a közlekedési rendszer biztonságát a járművek sebességének karakterisztikája is befolyásolja [14], [15], [16], azok átlagos értékeit és homogenitását is jellemző mutatókat képeztem.

 

Eddigi eredmények

Alapmodell kidolgozása

A forgalomszétosztás problémáját lineárisan leképezve olyan optimalizációs modellt dolgoztam ki, mellyel a felmerülő közlekedési igények a hálózat terheltségét optimalizálva valósíthatók meg. A közlekedési igények stratégiai szintű befolyásolása érdekében megvalósítottam a hálózat útvonalaihoz rendelt útdíjstruktúra modellbe integrálását. Az alapmodellek működését példahálózatokon validáltam, érzékenységvizsgálatot végeztem, megalapozva ezzel további vizsgálataimat.

 

A modell továbbfejlesztése

Az alapmodellt továbbfejlesztve, a közlekedési tér és az idő diszkretizációjával az autonóm közlekedési rendszer hálózati szintű optimalizálási feladatok megvalósítására is alkalmas, járműszintű irányítási modelljét dolgoztam ki. A kidolgozás során mikro (járműdinamikai korlátok) és makro (hálózati optimalizáció) szintű tényezőket egyaránt figyelembe vettem, leképezve a modellben a forgalom biztonságos lebonyolódásához szükséges feltételeket (pl. ütközések elkerülése, sávtartás, sebesség- és gyorsuláskorlátok). A modellt leíró matematikai összefüggéseket a MATLAB szoftverben implementáltam, működését és eredményeit különböző típusú útkereszteződéseket és több sávos útszakaszokat reprezentáló példahálózatokon értékeltem.

 

A szimulációs modell futásidejének csökkentése

A tér és idő mind részletesebb felbontása a számítási komplexitás jelentős növekedését okozza az optimalizáció során. A felosztás felbontásának növelése a problémát csökkenti, azonban egyúttal az optimalizáció hatékonyságát rontja. A modell futásidejének csökkentése érdekében ezért a korlátozó kifejezések számát csökkentő eljárásokat dolgoztam ki. A kialakított eljárásokkal kizárhatók a felesleges és redundáns ellenőrzések, és olyan lokációk vizsgálata, melyek az adott utazás kapcsán biztosan nem relevánsak (pl. a sebesség korlátozásából fakadóan nem érhetők el). A kidolgozott eljárások egyéni és kombinált hatásait példahálózatokon értékeltem, ellenőrizve azt is, hogy a módszerek a megoldás hatékonyságát és megbízhatóságát ne csökkentsék. Eredményeim alapján az eljárások a számítási komplexitás akár 84–96%-os csökkentését eredményezik.

 

Az autonóm közlekedési rendszerek biztonsági indikátorainak kidolgozása

A bemutatott modell segítségével alapot teremtettem az autonóm közlekedési rendszerekben végzett közlekedésbiztonsági elemzésekhez. Ehhez a forgalom lefolyásának biztonságát értékelő mutatókat határoztam meg. A kidolgozott indikátorok a keresztező járműmozgások számát és időbeli távolságát, továbbá a járművek egyéni és hálózati szintű sebességeinek értékeit és homogenitását vizsgálják. A mutatók egyrészt az optimalizáció során meghatározott forgalmi eloszlás biztonsági értékelésére és rangsorolására alkalmazhatók, másrészt lehetőséget teremtenek a különböző közlekedési hálózati struktúrák, vagy az azokon alkalmazott beavatkozások biztonságra gyakorolt hatásainak vizsgálatára.

 

A közlekedési hálózat leképezési struktúrájának hatásvizsgálata

A forgalmi menedzsment során hagyományosan alkalmazott négyzetrácsalapú leképezés mellett a közlekedési hálózat számos egyéb módon (pl. egyéb szabályos sokszögekkel) is strukturálható (4. ábra). A kidolgozott modell segítségével meghatároztam különböző hálózati struktúrák (pl. hatszögalapú, háromszögalapú leképezések) forgalmi hatékonyságra, számítási kapacitásra és biztonságra gyakorolt hatásait.

 

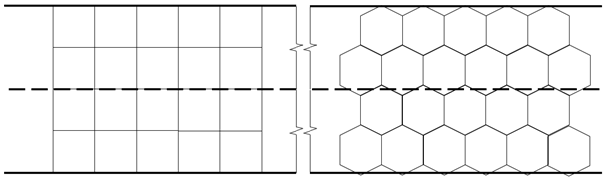
4. ábra: Példa egy egyszerű útszakasz különböző struktúrák szerinti leképezésére

A különböző struktúrák generálása az alap-poligonok köré írt további poligonok illesztésével történt. Az összehasonlíthatóságot az azonos sugarú beírható körrel jellemzett sokszögek alkalmazása biztosította. A számításokhoz a sokszögek és az azok közti kapcsolatok számát, a lefedett területet és a számítási komplexitást a hálózatgenerálás lépésszámainak függvényeként határoztam meg. Az eredményeim rámutattak arra, hogy a közúthálózat hagyományosan alkalmazott, négyzetrácsalapú leképezése több szempontból elmaradhat az egyéb sokszögek alkalmazásával kialakítható struktúrák jellemzőitől.

 

Várható impakt, további kutatás

A kutatás eredményei jelentős potenciállal bírnak a magasan automatizált közlekedési rendszerek forgalmának valós idejű, biztonságközpontú hatékony menedzselése terén. Az alapmodell és annak továbbfejlesztett változata impakt faktoros folyóiratokban került publikálásra, jelezve a témakör kutatásának fontosságát. A modell futásidejének csökkentésére, illetve a biztonság jellemzésére szolgáló módszertanok, valamint a hálózati struktúrák vizsgálatáról készült publikációk Q1-es folyóiratokban vannak elbírálás alatt.

További kutatásaink a hálózati leképezések automatizált megvalósítására és a jelenleg 2D-s eljárás 3D-s környezetre történő kiterjesztésére irányulnak. Ezáltal a módszertan a közlekedésen túlmutató egyéb területeken (pl. komplex UAV rendszerek menedzsmentje során) is hatékonyan alkalmazható megoldást nyújthatna.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája:

[S1] Pauer, G., Török, Á. (2019). Comparing System Optimum Based and User Decision Based Traffic Models in an Autonomous Transport System. Promet - Traffic & Transportation, 31(5), 581-589. DOI: https://doi.org/10.7307/ptt.v31i5.3151 (IF: 0,664)

[S2] Pauer, G., Török, Á. (2020). Binary integer modeling of the traffic flow optimization problem, in the case of an autonomous transportation system. Operations Research Letters, 49(1), 136-143. https://doi.org/10.1016/j.orl.2020.12.004 (IF: 0,757)

[S3] Pauer, G., Sipos, T., Török, Á. (2019). Statistical Analysis of the Effects of Disruptive Factors of Driving in Simulated Environment. Transport, 34(1), 1–8. DOI: https://doi.org/10.3846/transport.2019.6724 (IF: 1,053)

[S4] Pauer, G., Török, Á. (2022). Introducing a novel safety assessment method through the example of a reduced complexity binary integer autonomous transport model. Reliability Engineering & System Safety, 217, 108062. https://doi.org/10.1016/j.ress.2021.108062 (IF: 6,188)

[S5] Pauer, G., Török, Á. (2021 – benyújtva, elbírálás alatt). The impact of grid structures on decision support processes in future transport systems. Decision Support Systems (IF: 4,721)

[S6] Pauer, G., Török, Á. (2019). Static System Optimum of Linear Traffic Distribution Problem Assuming an Intelligent and Autonomous Transportation System. Periodica Polytechnica Transportation Engineering, 47(1), 64–67. DOI: https://doi.org/10.3311/PPtr.11548

[S7] Török, Á., Pauer, G. (2018). Optimization of Linear Traffic Distribution Problem in terms of the Road Toll Structure Assuming an Autonomous Transportation System. International Journal for Traffic and Transport Engineering, 8(1), 112–124. DOI: 10.7708/ijtte.2018.8(1).08

[S8] Török, Á., Pauer, G. (2017). Assessment of the Current Status of Intelligent Transport Systems Serving the Improvement of Road Safety in Hungary. Periodica Polytechnica Transportation Engineering, 45(2), 19–24. DOI: 10.3311/PPtr.9279

[S9] Pauer, G. (2017). Development Potentials and Strategic Objectives of Intelligent Transport Systems Improving Road Safety. Transport and Telecommunication, 18(1), 15–24. DOI: https://doi.org/10.1515/ttj-2017-0002

[S10] Pauer, G., Berta, T., Török, Á. (2017). Analysing the Impact of Road Safety Information System on Traffic Safety. Transbaltica 2017: Transportation Science and Technology, Procedia Engineering, Volume 187, 712-721. Vilnius, Litvánia. DOI: https://doi.org/10.1016/j.proeng.2017.04.445

[S11] Pauer, G. (2017). Defining the Optimization Process of Traffic Distribution Problem with Linear Programming Approach in case of Autonomous Transportation System. In MOSATT 2017 Modern Safety Technologies in Transportation: Proceedings of the International Scientific Conference, 124-130. Herlány, Szlovákia. ISBN 978-80-553-2864-5.

[S12] Török, Á., Pauer, G. (2016). Intelligens közlekedési rendszerek közlekedésbiztonsági rangsorolása. Statisztikai Szemle, 94(4), 418–434. DOI: 10.20311/stat2016.04.hu0418

[S13] Pauer, G., Török, Á. (2019). Forgalom optimalizáció különböző felépítésű hálózatokon autonóm közlekedési rendszerben. IX. Közlekedéstudományi Konferencia, Győr, Magyarország.

 

Linkgyűjtemény:

https://auto.bme.hu/

https://auto.bme.hu/kutatas/#biztonsag-es-vedelem

 

Hivatkozások listája:

[1] Tettamanti, T., Varga, I., Szalay, Z. (2016). Impacts of autonomous cars from a traffic engineering perspective. Periodica Polytechnica Transportation Engineering, 44(4), 244–250. https://doi.org/10.3311/PPtr.9464

[2] Speranza, M.G. (2018). Trends in transportation and logistics. European Journal of Operational Research, 264(3), 830–836. https://doi.org/10.1016/j.ejor.2016.08.032

[3] Zöldy, M. (2018). Investigation of autonomous vehicles fit into traditional type approval process. Proceedings of ICTTE, Belgrade, Serbia, 428–432.

[4] Levin, M.W., Odell, M., Samarasena, S., Schwartz, A. (2019). A linear program for optimal integration of shared autonomous vehicles with public transit. Transportation Research Part C: Emerging Technologies, 109, 267–288. https://doi.org/10.1016/j.trc.2019.10.007

[5] Cokyasar, T., Larson, J. (2020). Optimal assignment for the single-household shared autonomous vehicle problem. Transportation Research Part B: Methodological, 141, 98–115. https://doi.org/10.1016/j.trb.2020.09.003

[6] Van Brummelen, J., O’Brien, M., Gruyer, D., Najjaran, H. (2018). Autonomous vehicle perception: The technology of today and tomorrow. Transportation research part C: emerging technologies, 89, 384–406. https://doi.org/10.1016/j.trc.2018.02.012

[7] Javed, M.A., Zeadally, S., Hamida, E.B. (2019). Data analytics for cooperative intelligent transport systems. Vehicular communications, 15, 63–72. https://doi.org/10.1016/j.vehcom.2018.10.004

[8] Jacobstein, N. (2019). Autonomous vehicles: An imperfect path to saving millions of lives. Science robotics, 4(28), eaaw8703. DOI: 10.1126/scirobotics.aaw8703

[9] Li, L., Wang, X., Wang, K., Lin, Y., Xin, J., Chen, L., Wang, F.Y. (2019). Parallel testing of vehicle intelligence via virtual-real interaction. Science robotics, 4(28), eaaw4106. DOI: 10.1126/scirobotics.aaw4106

[10] Elfes, A. (1989). Occupancy grids: A probabilistic framework for robot perception and navigation. Ph.D Thesis, Carnegie-Mellon University, Pittsburgh, PA.

[11] Rakotovao, T., Mottin, J., Puschini, D., Laugier, C. (2015). Real-Time Power-Efficient Integration of Multi-Sensor Occupancy Grid on Many-Core. Proceedings of the 2015 IEEE International Workshop on Advanced Robotics and its Social Impacts (ARSO), Lyon, France, 1-6. DOI: 10.1109/ARSO.2015.7428211

[12] Daudelin, J., Jing, G., Tosun, T., Yim, M., Kress-Gazit, H., Campbell, M. (2018). An integrated system for perception-driven autonomy with modular robots. Science robotics, 3(23), eaat4983. DOI: 10.1126/scirobotics.aat4983

[13] Ramakrishnan, S.K., Jayaraman, D., Grauman, K. (2019). Emergence of exploratory look-around behaviors through active observation completion. Science robotics, 4(30), eaaw6326. DOI: 10.1126/scirobotics.aaw6326

[14] van Nes, N., Brandenburg, S., Twisk, D. (2010). Improving homogeneity by dynamic speed limit systems. Accident Analysis & Prevention, 42(3), 944–952. https://doi.org/10.1016/j.aap.2009.05.002

[15] Yu, R., Abdel-Aty, M. (2014). An optimal variable speed limits system to ameliorate traffic safety risk. Transportation Research Part C: Emerging Technologies, 46, 235–246. https://doi.org/10.1016/j.trc.2014.05.016

[16] Pauer, G., Sipos, T., Török, Á. (2019). Statistical Analysis of the Effects of Disruptive Factors of Driving in Simulated Environment. Transport, 34(1), 1–8. https://doi.org/10.3846/transport.2019.6724