Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék

Témavezető: Dr. Insperger Tamás

Egyensúlyozó deszkán való egyensúlyozás modellezése a frontális síkban

A kutatási téma néhány soros bemutatása

Idősödő társadalmunkban egyre gyakoribbá válnak az egyensúlyvesztésből adódó balesetek, amelyek akár halálos kimenetelűek is lehetnek. Az érzékszervek érzékelési pontosságának romlása, a mozgásszegény életmód, az izomzat gyengülése és a reakcióidő megnövekedett értéke mind növelik az egyensúlyvesztés kockázatát idős korban [1]. A balesetek megelőzéséhez elengedhetetlen a központi idegrendszer működésének megértése, amelyhez segítséget nyújthat egyszerű egyensúlyozási feladatok dinamikai vizsgálata és egyensúlyozási kísérletek mozgásanalízise.

A kutatóhely rövid bemutatása

Kutatásaimat Insperger Tamás témavezetésével végeztem a Műszaki Mechanikai Tanszéken az MTA-BME Lendület Emberi Egyensúlyozás Kutatócsoportban. A kutatócsoport célja megérteni és modellezni a központi idegrendszer szabályozási stratégiáját egyszerű egyensúlyozási feladatok közben. Alacsony szabadsági fokkal modellezhető feladatokat vizsgálunk mechanikai és kísérleti módszerekkel. Az eredmények alapján egyensúlyfejlesztő eszközöket, terápiákat ajánlunk.

A kutatás történetének, tágabb kontextusának bemutatása

A mindennapjainkban megjelenő statikus vagy dinamikus mozgásformák, például az állás, ülés vagy a járás instabil egyensúlyi helyzetek körül történnek. Az emberi test stabilizálása a központi idegrendszer feladata. Egyensúlyozás közben a vizuális, a vesztibuláris és a szomatoszenzoros rendszerek, a szem, a fül és a bőr megfelelő receptorai érzékelik a testrészek helyzetét és sebességét. A receptorok által biztosított jelek alapján a központi idegrendszer meghatározza az egyensúly megtartásához szükséges beavatkozást, amit az izomzat végrehajt. Az információ idegpályákon, idegrostokon történő szállítása és feldolgozása időt igényel, a folyamatban megjelenik a reakcióidő. A központi idegrendszer működését gyakran modellezik időkésleltetett arányos-deriváló (PD) szabályozásként, ahol a visszacsatolás időkésése a reakcióidőnek felel meg [2-4].

Egy egyensúlyozási feladat sikerességét meghatározza az ún. kritikus időkésés. Ha a visszacsatolás időkésése nagyobb a kritikus értéknél, akkor az egyensúlyi helyzet nem stabilizálható. Az ujjhegyen való rúdegyensúlyozás feladatára a kritikus időkésés függ a rúd hosszától, amennyiben az ujjhegyről a rúd aljára átadódó szabályozási erőt PD visszacsatolásként modellezzük. Egy 30 cm hosszúságú rúdra a kritikus időkésés 200 ms. Ha az egyensúlyozó személy reakcióideje 200 ms-nál nagyobb, nem képes egyensúlyozni a rudat.

Egyhelyben állás esetén a boka körüli izmok és inak passzív merevsége az emberi reakcióidő közelítőleg négyszeresére növeli a kritikus időkésést. Annak érdekében, hogy a kritikus időkésés értéke csökkenjen, egy változtatható keréksugárral rendelkező gördülő egyensúlyozó deszkát alkalmazunk a kutatásban (1. ábra).

 

1.      ábra: A kutatásban alkalmazott, változtatható keréksugárral rendelkező egyensúlyozó deszka.

 

A kutatás célja, a megválaszolandó kérdések

Jelen tanulmány a keréksugár és a terpeszszélesség változásának az egyensúlyozási feladat nehézségére gyakorolt hatására fókuszál. Egészséges, fiatal felnőttek egyensúlyozási kísérletein keresztül vizsgáltam a keréksugár és a terpeszszélesség hatását a frontális, vagyis az oldalra dőlés síkjában (2.c ábra). A mérés előtt a testrészekre és az egyensúlyozó deszkára reflektív markereket helyeztem, OptiTrack mozgáskövető rendszerrel rögzítettem a kísérleteket.

Felépítettem az egyensúlyozó deszkán való egyensúlyozás frontális síkra érvényes két és három szabadsági fokú mechanikai modelljét (2.a–b ábra). A gördülő egyensúlyozó deszka mindkét modellben egy-egy szabadsági foknak felel meg. A két szabadsági fokú modellben a második szabadsági fokot az emberi testet modellező négycsuklós mechanizmus jelenti. A három szabadsági fokú modell figyelembe veszi a felsőtest és az alsó végtagok relatív mozgását, tehát az emberi test modellje két szabadsági fokú. A biomechanikai szakirodalom az emberi test egy, illetve két szabadsági fokú modelljére boka, illetve boka-csípő stratégiaként hivatkozik [5].

Az alábbi három hipotézist állítottam fel.

H1. Azon keréksugár–terpeszszélesség kombinációk mellett nehezebb egyensúlyozni, amelyekhez kisebb kritikus időkésés tartozik.

H2. A reakcióidő becsülhető közvetett módon a modellből kapott kritikus időkésésekből és különböző keréksugár-terpeszszélesség kombinációk mellett végzett sikeres és sikertelen egyensúlyozási kísérletekből.

H3. A boka–csípő stratégia alkalmazása előnyösebb a boka stratégiával szemben abban az értelemben, hogy a boka–csípő stratégiát feltételező modellre nagyobbak a kritikus időkésések.

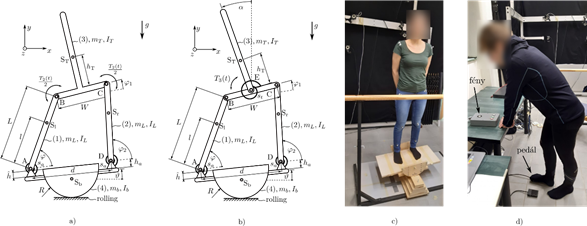
2.      ábra. a) Az egyensúlyozó deszkán való egyensúlyozás két szabadsági fokú modellje a frontális síkban. b) Az egyensúlyozó deszkán való egyensúlyozás három szabadsági fokú modellje a frontális síkban. c) A vizsgált egyensúlyozási feladat. d) Vizuális ingerre végzett válaszidő mérés.

 

Módszerek

Tíz alany bevonásával méréseket végeztem. Egy statikus teszttel mértem a vizsgálati alanyok vizuális ingerre adott válaszidejét. A résztvevőt arra kértem, hogy a méréshez használt eszközön található fényforrás felvillanása után amilyen gyorsan lehetséges, domináns lábfejével nyomja le az eszközhöz csatlakoztatott pedált (2.d ábra). A válaszidő a felvillanás és a pedál lenyomása között eltelt idő, tíz mérés átlaga. Ezután a vizsgálati alanyok fél perces egyensúlyozási kísérleteket hajtottak végre nyitott szemmel, nyújtott lábbal hat kiválasztott keréksugár (20, 15, 12.5, 10, 7 és 5 cm) és három terpeszszélesség (40, 25 és 15 cm) mellett. A lap talajtól mért magassága 5 cm volt.

A mechanikai modellekben a testek közötti csuklók a boka- és csípőízületeknek, illetve a gerincoszlop alsó részének felelnek meg, amelyek passzív merevségét lineáris karakterisztikájú torziós rugóval modelleztem. Az emberi test paramétereit és a merevségek értékét szakirodalmi adatok alapján számítottam [6-9]. A szabályozó nyomaték a csípőnél jelenik meg mindkét modellben. Feltételeztem, hogy a központi idegrendszer a szabadsági fokokhoz tartozó merev testek dőlésszöge és szögsebessége alapján határozza meg a szükséges beavatkozást, tehát időkésleltetett PD szabályozásként modellezhető. A két szabadsági fokú modell esetén ez négy, a három szabadsági fokú modellnél hat erősítési tényezőt jelent. Az egyszerűség kedvéért a különböző érzékszervekből érkező információkat nem különböztettem meg időkésésük szerint, egy ún. konstans, egyenértékű időkésést vezettem be.

A két modell linearizált mozgásegyenlete egy-egy késleltetett differenciálegyenlet-rendszer. A felső egyensúlyi helyzet stabilitásának feltétele, hogy a karakterisztikus egyenlet végtelen számú gyöke a komplex sík bal oldalán helyezkedjen el. Az emberi test és az egyensúlyozó deszka paramétereit rögzítve a stabilitás csak az időkésés és a szabályozó paraméterek megválasztásától függ. Rögzített időkésésre a szabályozó paramétereknek létezik egy négy, illetve hat dimenziós stabilizáló tartománya. Növekvő időkésésre a tartomány csökken, majd az ún. kritikus időkésésre egyetlen ponttá zsugorodik. A kritikusnál nagyobb időkésésre az erősítési tényezőktől függetlenül instabil az egyensúlyi helyzet.

A kritikus időkésés kapcsolatban van az egyensúlyozási kísérletekkel. Ha egy alany reakcióideje nagyobb, mint egy adott keréksugár-terpeszszélesség párhoz tartozó kritikus időkésés, akkor stabilizáló paraméterek hiányában az egyensúlyozás sikertelen. Egy analitikus, a karakterisztikus egyenlet domináns gyökének multiplicitásán alapuló módszerrel [10-11] kiszámítottam a kritikus időkéséseket a mérésnél vizsgált keréksugár–terpeszszélesség tartományon. Az eredmény, az ún. stabilizálhatósági diagramok a 3. ábrán láthatóak. A kritikus időkésés változását szürke színskála mutatja. A diagramok jobb alsó, fehér tartományán a szabályozás nélküli rendszer tulajdonságai nem teljesítik az analitikus módszer alkalmazhatóságának feltételeit. A fehér tartomány keréksugár–terpeszszélesség pontjaihoz nem tartoznak kritikus időkésések, azonban ez nem releváns a konklúzió szempontjából.

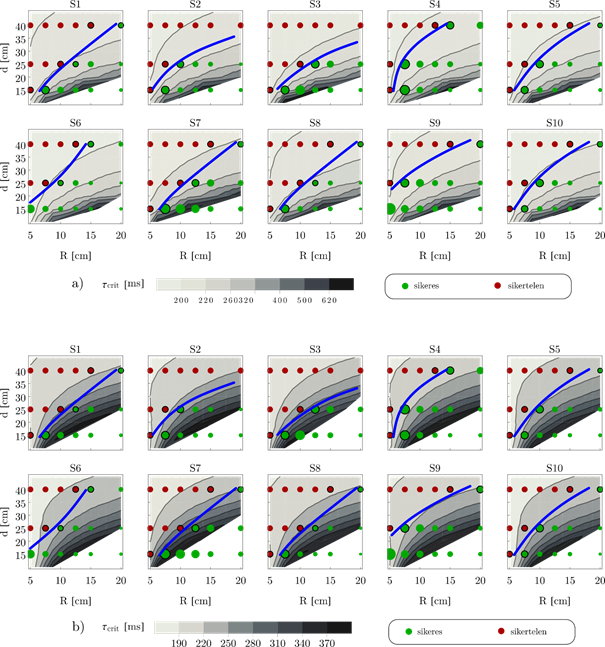
3.      ábra. a) Stabilizálhatósági diagramok a két szabadsági fokú modellre. b) Stabilizálhatósági diagramok a három szabadsági fokú esetre.

Eddigi eredmények

A résztvevők sikeres és sikertelen egyensúlyozási kísérleteit zöld és piros jelölő, határukat kék görbe jelöli a 3. ábrán. A keréksugár csökkentésével és a terpeszszélesség növelésével egyre nagyobb kihívást jelentett a feladat. A reakcióidő becslése közvetlenül a határgörbe mellett elhelyezkedő, fekete körvonallal jelölt pontokhoz tartozó kritikus időkésések átlagolásával történt. A becsült reakcióidők a 4. ábrán láthatóak: kék szín felel meg a két, piros a három szabadsági fokú modell és a kísérletek összehasonlításából becsült reakcióidőknek. A válaszidőmérés eredményeit feketével ábrázoltam. A mért válaszidő az összes alany esetében nagyobb, mint a modellek alapján becsült reakcióidő. Ez azzal magyarázható, hogy a válaszidő a reakcióidő (a fénykibocsátás és a lábfej izmainak összehúzódása között eltelt idő) és a mozdulat, vagyis a pedálnyomás idejének az összege, míg a matematikai modell alapján tisztán a reakcióidő becsülhető.

A tíz alany két, illetve három szabadsági fokú modell alapján becsült reakcióideje 198–239 ms (átlag: 214 ms) és 201–282 ms (átlag: 228 ms), tehát nagyobbak, mint az egyhelyben állásra érvényes szakirodalmi adatok (90–125 ms) [12–15]. A különbség egyrészt azzal magyarázható, hogy egyensúlyozó deszkán való egyensúlyozás közben összetettebb jeleket dolgoz fel a központi idegrendszer, ami hosszabb időt igényel. Másrészt, a matematikai modellben nem vettem figyelembe az érzékszervek érzékelési pontatlanságát, amely kiegészítés csökkentené a becsült reakcióidőket.

A H1 hipotézis elfogadásra került. A 3. ábrán a zöld és piros jelölők területe egyenesen arányos az egyensúlyozó deszka szögének aktuális szórásával. A szórásra úgy is tekinthetünk, mint az egyensúlyozási feladat nehézségének mérőszáma: minél nagyobb a szórás, annál nehezebb a feladat. A stabilizálhatósági diagramokon látható, hogy a kritikus időkésés csökkenésével egyre gyakoribbak a sikertelen egyensúlyozási kísérletek és tipikusan nő az egyensúlyozó deszka szögének szórása, ez megerősíti a H1 hipotézist.

A H2 hipotézis is elfogadásra került. A hipotézist alátámasztja egyrészt, hogy a sikeres és sikertelen egyensúlyozási kísérletek kék határvonala illeszkedik a stabilizálhatósági diagram szintvonalainak struktúrájába. Másrészt, a két modell alapján becsült reakcióidő és a mért válaszidő közötti erős korreláció (a korrelációs együttható 0,77, illetve 0,78) következménye, hogy a stabilizálhatósági diagram és az egyensúlyozási kísérletek alapján közvetetten becsülhető a reakcióidő.

A H3 hipotézis a nehéz feladatokra elfogadható. A stabilizálhatósági diagramok alapján megállapítható, hogy a könnyű feladatokra (nagy keréksugár, szűk terpesz) a két szabadsági fokú modellből nagyobb kritikus időkésések adódtak. Nehéz feladatokra (kis keréksugár, széles terpesz) azonban valóban nagyobbak a kritikus időkésések a három szabadsági fokú modell, tehát a boka–csípő stratégia esetén.

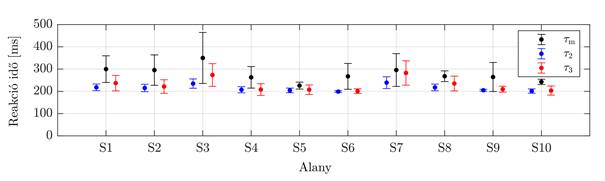
4.      ábra. A stabilizálhatósági diagramok és az egyensúlyozási kísérletek alapján becsült reakcióidők és a mért válaszidők.

 

Várható impakt, további kutatás

A bemutatott eredményeket egy rangos biomechanikai nemzetközi folyóiratban tervezzük publikálni; a cikk benyújtás előtt áll. A matematikai modell tartalmazza a balesetek hátterében álló leggyakoribb tényezőket, a reakcióidőt és az izomzat fizikai tulajdonságait, később kiegészíthető az érzékszervek érzékelési bizonytalanságával. A jövőben elvégezzük a méréseket egyensúlyzavarral küzdő alanyok bevonásával, és stratégiát dolgozunk ki az egyensúlyzavart okozó tényező azonosítására a stabilizálhatósági diagram és a kísérletek alapján. Az egyensúlyozó deszka a változtatható, jól definiált paraméterek miatt alkalmas az egyensúlyozási képesség monitorozására. Célunk kidolgozni egy gyakorlatsorozatot, amely hozzájárulhat az egyensúlyozási képesség fejlődéséhez és a már bekövetkezett baleseteket követő intenzív rehabilitációhoz.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája

 

S1. Molnar CA, Zelei A, Insperger T. Rolling balance board of adjustable geometry as a tool to assess balancing skill and to estimate reaction time delay. Journal of the Royal Society Interface 2021; 18(176):20200956. (IF=3,748)

S2.  Molnar CA, Balogh T, Boussaada I, Insperger T. Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control 2021; 27(3-4):356–64. (IF=2,169)

S3.  Molnar CA, Insperger T. Parametric study of changes in human balancing skill by repeated balancing trials on rolling balance board. Periodica Polytechnica Mechanical Engineering 2020; 64(4):317–27.

S4.  Wang Z, Liang S, Molnar CA, Insperger T, Stepan G. Parametric continuation algorithm for time-delay systems and bifurcation caused by multiple characteristic roots. Nonlinear Dynamics 2021; 103(4):3241–53. (IF=4,867)

S5. Molnar CA, Insperger T. Estimation of reaction time during human balancing on rolling balance board based on mechanical models. in: International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 2020; 83914:V002T02A033, online.

S6.  Molnar CA, Insperger T. Egyensúlyozási képességek fejlődésének vizsgálata egyensúlyozó deszkán. in: XIII. Magyar Mechanikai Konferencia 2019; p 4, Miskolc.

S7.  Molnar CA, Varszegi B, Insperger T. Identification of sensory dead zones in human balancing on balance board. in: Proceedings of the European Control Conference (ECC) 2019; 2904–2909., Nápoly.

S8.  Molnar CA, Zelei A, Insperger T. Human balancing on rolling balance board in the frontal plane. in: IFAC-PapersOnLine 2018; 51(14):300–305., Budapest.

S9.  Molnar CA, Zelei A, Insperger T. Mechanical model for human balancing on rolling balance board. Acta Polytechnica CTU Proceedings 2018; 18:32–37.

S10.  Zelei A, Molnar CA, Insperger T. Four-bar mechanism substitution for balance board experiments: A parametric study. in: Proceeding of the Dynamical Systems in Applications 2018; 473–484., Lódz.

S11. Molnar CA, Zelei A, Insperger T. Egyensúlyozó deszkán való egyensúlyozási képességek modellezése a sagittalis síkban. in: OGÉT 2017: 25th International Conference on Mechanical Engineering 2017; 283–286. Kolozsvár.

 

 

Linkgyűjtemény

 

Műszaki Mechanikai Tanszék honlapja

MTA-BME Lendület Emberi Egyensúlyozás Kutatócsoport honlapja

 

Hivatkozások listája

 

[1]    Robinovitch SN, Feldman F, Yang Y, Schonnop R, Leung PM, Sarraf T, Sims-Gould J, Loughin M. Video capture of the circumstances of falls in elderly people residing in long-term care: an observational study. The Lancet 2013; 381(9860):47–54.

[2] Mehta B, Schaal S. Forward models in visuomotor control. Journal of Neurophysiology 2002; 88(2):942–53.

[3] Maurer C, Peterka JP. A new interpretation of spontaneous sway measures based on simple model of human postural control. Journal of Neurophysiology 2005; 93:189–200.

[4] Stepan G. Delay effects in the human sensory system during balancing. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2009; 367(1891):1195–212.

[5] Runge CF, Shupert CL, Horak FB, Zajac FE. Ankle and hip postural strategies defined by joint torques. Gait & Posture.1999; 10(2):161–70.

[6] Trevino J, Lee H. Sex differences in 2-DOF human ankle stiffness in relaxed and contracted muscles. Annals of Biomedical Engineering 2018; 46(12):2048–56.

[7] Nalam V, Adjei E, Lee H. Quantification and Modeling of Ankle Stiffness During Standing Balance. IEEE Transactions on Biomedical Engineering 2020; 68(6):1828–37.

[8] McGill S, Seguin J, Bennett G. Passive stiffness of the lumbar torso in flexion, extension, lateral bending, and axial rotation. Effect of belt wearing and breath holding. Spine 1994; 19(6):696–704.

[9] De Leva P. Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. Journal of Biomechanics 1996; 29(9):1223–30.

[10] Molnar CA, Balogh T, Boussaada I, Insperger T. Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control 2021; 27(3-4):356–64.

[11] Boussaada I, Niculescu SI. On the dominancy of multiple spectral values for time-delay systems with applications. IFAC-PapersOnLine 2018; 51(14):55–60.

[12] Kiemel T, Oie KS, Jeka JJ. Slow dynamics of postural sway are in the feedback loop. Journal of Neurophysiology 2006; 95(3):1410–8.

[13] Li Y, Levine WS, Loeb GE. A two-joint human posture control model with realistic neural delays. IEEE Transactions on Neural Systems and Rehabilitation Engineering 2012; 20(5):738–48.

[14] Pasma JH, Boonstra TA, van Kordelaar J, Spyropoulou VV, Schouten AC. A sensitivity analysis of an inverted pendulum balance control model. Frontiers in Computational Neuroscience 2017; 11:99.

[15] Milton J, Insperger T. Acting together, destabilizing influences can stabilize human balance. Philosophical Transactions of the Royal Society A 2019; 377(2153):20180126.