Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék

Témavezető: Dr. Stépán Gábor

Esztergálási folyamat stabilitásvizsgálata környezetszimulációval

A kutatási téma néhány soros bemutatása

Esztergálási és marási anyagleválasztó megmunkálások során úgynevezett öngerjesztett regeneratív rezgések léphetnek fel, melyek mind a munkadarab, mind pedig a szerszám rugalmasságához köthetők. Ezek a kis amplitúdójú rezgések [C1,P1] nem csupán ronthatják a munkadarab felületi minőségét, de a szerszámgépet is károsíthatják (1. ábra (a)). A szerszámgép valós dinamikája mellett, a szerszám/munkadarab kölcsönhatást beavatkozókkal előállítva, a megmunkálás szempontjából releváns paraméter tartományban a rezgések jelentkezése környezetszimulációs berendezés (Hardware-in-the-Loop, HIL, 1. ábra (b)) segítségével vizsgálható [R1]. Ez egy nagy teljesítményű, számítógéppel segített, jól vezérelhető félvirtuális lehetőséget biztosít az esetlegesen fellépő negatív hatások (szerszámtörés, főorsó károsodás) előrejelzéséhez és a rezgésmentes tartományban az adott folyamattal elérhető legnagyobb anyagleválasztási arány meghatározásához.

1. ábra: (a) Megmunkálási folyamat során ébredő kis amplitúdójú, káros rezgés. (b) Környezetszimulációs (HIL) berendezés.

 

A kutatóhely rövid bemutatása

A kutatómunkát a BME GPK Műszaki Mechanikai Tanszékén végzem és végeztem, részben a Dr. Stépán Gábor által vezetett SIREN ERC kutatócsoport (2013-2019) munkája keretein belül. A kutatócsoport célja a megmunkálási folyamatok során ébredő dinamikai hatások és a forgácsleválasztás matematikai modellezése és ennek alapján a vágási folyamat rezgésmentes (stabil) paraméter tartományának pontos meghatározása. A tanszék szoros kapcsolatban áll a kutatási terület vezető nemzetközi szakértőivel, kutatóhelyeivel.

A kutatás történetének, tágabb kontextusának bemutatása

A szerszámgéprezgések az 1900-as évek elején kezdték foglalkoztatni a kutatókat, de a rezgések okának azonosítása, matematikai modellezése csak az 1950-es években kezdődött el [R2,R3]. Anyagleválasztáskor mind a munkadarab, mind a szerszám rugalmassága nagy frekvenciájú öngerjesztett rezgésekhez (chatter) vezethet. Esztergálási (vagy marási) folyamatok esetén a munkadarab (vagy szerszám) körülfordulása után a szerszám találkozik “előéletével”: ez a munkadarab hullámos felületeként megjelenő gerjesztés, ami őrzi a szerszám/munkadarab múltbéli relatív mozgását. Ez a regeneratív dinamika káros rezgések formájában korlátozza a szerszámgépek termelékenységét [R4].

 

A stabil paramétertartomány megadható a késleltetett differenciálegyenletek stabilitásvizsgálatával. Mindezek gyakorlati alkalmazása kevéssé terjedt el a paraméterek bizonytalansága és a drága, időigényes kísérleti meghatározásuk miatt. Két megoldási lehetőség adódik. Létrehozhatunk egy virtuális megmunkáló központot, ahol tetszőleges paraméterekkel szimulálhatjuk a megmunkálást és ezzel segíthetjük a tényleges folyamat paramétereinek beállítását [R5]. Ennek hátránya, hogy a szimuláció jelentősen függ az anyagleválasztás és a szerszámgép adaptált mechanikai modelljeitől.

 

Másrészt vizsgálhatjuk a problémát egy számítógéppel vezérelt valós környezetben, ahol a forgácsolást a szerszámgép valós dinamikájával, de a szerszám/munkadarab kölcsönhatást elektromágneses beavatkozókkal és lézer érzékelőkkel helyettesítve emuláljuk [R1]. Ezzel létrehozható egy félvirtuális környezetszimulációs kísérleti berendezés, amellyel a megmunkálási folyamatok rezgésmentes tartományai gyorsan, nagy pontossággal megadhatók, elkerülve a berendezés esetleges károsodását. Egy ilyen egyedülálló berendezés készült el az ERC projekt keretében.

A kutatás célja, a megválaszolandó kérdések

A stabil paramétertartomány növelése érdekében egyre több kutatás folyik speciális szerszámgeometria vagy a szerszámgéphez kapcsolódó kiegészítő szerkezeti elemek alkalmazásával. Ezek egyes esetekben stabil szigetekhez/csatornákhoz vezetnek és jellemzően magas anyagleválasztási aránynál jelennek meg az eredetileg rezgésekkel terhelt (instabil) tartományon belül [R6]. A stabil formációk kísérleti úton való megtalálásához instabil tartományok keresztezésére van szükség, ami nemkívánatos tranziens rezgéseket okozhat. Ez széles körű laboratóriumi teszteket igényel nagy mennyiségű prototípus bevonásával.

 

Mivel a megmunkálási folyamatok rezgésmentes tartományai nem csupán az adott szerszám és a munkadarab kapcsolatától, hanem a szerszámgép viselkedésétől is függnek, a főorsó dinamikájának azonosítása és figyelembevétele elengedhetetlen a pontos vizsgálat szempontjából. Kismértékű belső vagy külső zavarás (hőmérsékletváltozás, kenés, szerszám/szerszámbefogó illesztései) hatására jelentősen változhatnak a stabil tartományok határai.

 

Ezek kezeléséhez célszerű a környezetszimulációs kísérleti berendezés alkalmazása [P2]. Az eszköz a szerszám/munkadarab kölcsönhatástól függően, valós főorsó-dinamika mellett képes kísérletileg vizsgálni az adott folyamat rezgésmentes tartományát. Ez a forgácsoló szerszám és a munkadarab közötti kapcsolat mérésével meghatározott forgácsolóerő-karakterisztikák és a szerszámgeometria programozásával valósítható meg. Célszerű lehet a szerszámél-geometria működés közbeni, a stabil tartomány növelését célzó optimalizálása is. A környezetszimulációs berendezés segítségével az elméleti modellek megbízhatóságát is növelhetjük, például a szerszámgép mérésekkel meghatározott, fordulatszámfüggő dinamikai viselkedésének adaptálásával.

Módszerek

A környezetszimulációs eszköz segítségével emulált megmunkálási folyamatoknál nincs szükség egyéb külső hardveres vagy szoftveres környezetre a rendszer mechanikai paramétereinek identifikálásához, ami a beépített beavatkozóknak és szenzoroknak köszönhető. A kísérleti berendezés (ld.: 2. ábra (b)) egy 18 krpm névleges fordulatszámú, 2 kW teljesítményű Teknomotor főorsót, egy ER25 típusú szerszámbefogót, lézeralapú érzékelőket és elektromágneses beavatkozókat tartalmaz. A főorsó hibrid, radiális kerámia csapágyakkal van szerelve, szabályozása pedig egy OMRON JZAB1P5BAA frekvenciaváltó segítségével történik. A virtuális forgácsolóerő emulálását az elektromágneses beavatkozók végzik, a befogott munkadarab/szerszám deformációját lézeres érzékelők mérik.

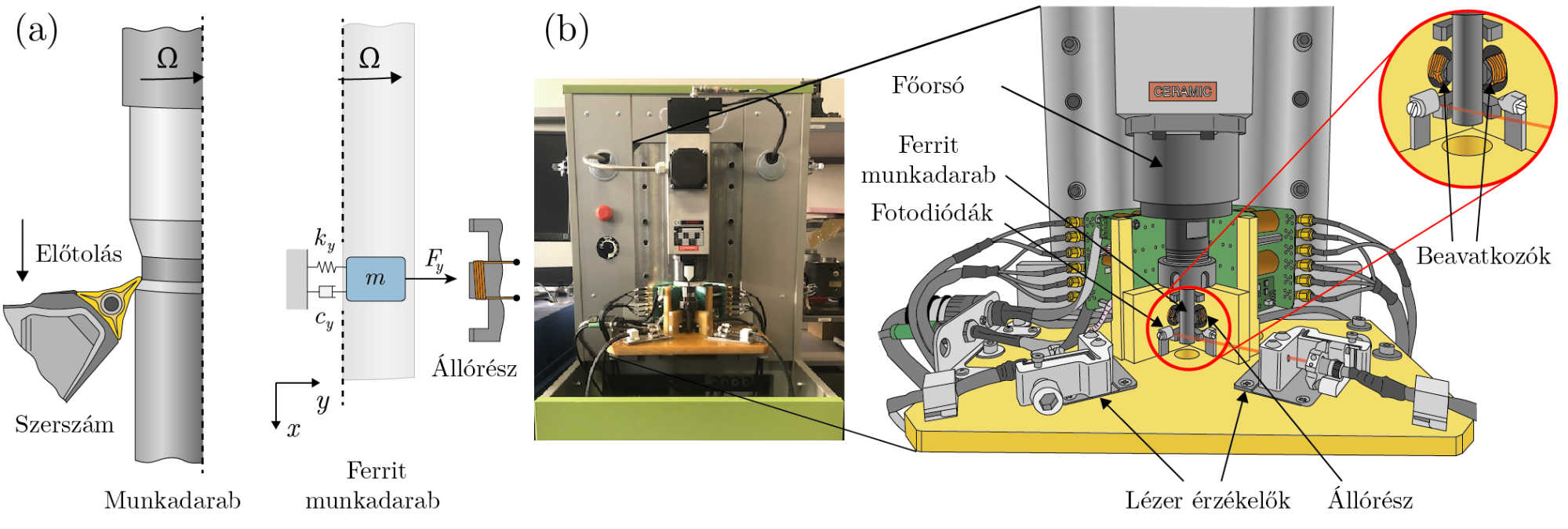
2. ábra: (a) Valós esztergálási folyamat és rugalmas munkadarabbal [C3,P3,P4] közelített egy szabadsági fokú (1 DoF) mechanikai modellje fél-virtuális környezetben. (b) Környezetszimulációs berendezés. [P2,P5]

 

Mechanikai paraméterek azonosítása

A kutatás során a HIL eszköz dinamikáját a főorsó fordulatszámának függvényében vizsgáljuk a beépített elektromágneses beavatkozók által emulált söprő szinuszos jel segítségével. Ekkor az általunk relevánsnak tekintett frekvenciatartományban gerjesztjük a rugalmas munkadarabot [P3,P4], és mérjük a rendszer gerjesztésre adott válaszát [P2,C2,P5]. A mérési eredmények segítségével létrehozhatók a rendszer viselkedését jellemző frekvenciaátviteli függvények (FRF) és a fordulatszámfüggő dinamikát bemutató Campbell-diagram (ld. 3. ábra) [R7,P2,C2,P5]. Ezzel a módszerrel azonosíthatóvá válnak a szerszámgép főbb módusai és az azokhoz tartozó mechanikai paraméterek [P2].

 

Elméleti stabilitásvizsgálat

A rendszeridentifikáció lehetőséget biztosít elméleti mechanikai modellek létrehozására, beleértve a virtuális forgácsolóerő adaptálását is. A szerszám adott pillanatbeli és múltbeli pozíciójától is függő leválasztott forgácsvastagság okozza a forgácsolóerő megváltozását, és ennek megfelelően a matematikai modell egy késleltetett differenciálegyenlet [R2]. A vizsgálat magában foglalja azokat az eseteket is, amikor a munkadarab/szerszám rugalmassága [C3,C4,P3,P4] vagy az emulált forgácsolóerő nemlinearitása [C2,P5] hatására megváltozik a rendszer domináns frekvenciája. A rendszer stabilitásvizsgálata a főorsó-fordulatszám és virtuális forgácsszélesség paramétertartományra vonatkozik [C3,C4]. A stabil paraméterpárok meghatározása frekvencia- és időtartományban is elvégezhető az úgynevezett D-szeparációs és/vagy szemidiszkretizációs (SD) matematikai módszerek segítségével (ld. 4. ábra) [R8,P2].

 

Kísérleti stabilitásvizsgálat (Chatter teszt)

Az emulált folyamat stabilitásvizsgálata elméleti modellek alkalmazása nélkül is megvalósítható. Tetszőleges fordulatszám és virtuális forgácsszélesség paraméterpárokra egy automatizált, pontonként kb. 3 s időtartamú teszt végezhető el. Ekkor az emulált forgácsolóerőre adott munkadarabelmozdulás-válaszjelet gyors Fourier transzformálva (FFT) megállapítható a folyamat domináns rezgési frekvenciája [P2,C2,P5]. A környezeti alacsony frekvenciás rezgéseket figyelmen kívül hagyva, az általunk választott tartományon megadhatók a rezgésmentes (stabil) paraméterpontok (ld. 4. ábra).

 

Eddigi eredmények

Fordulatszámfüggő dinamika kísérleti azonosítása

A szerszámgép főorsójának működés közbeni dinamikáját a környezetszimulációs berendezésbe épített beavatkozók és érzékelők segítségével valós időben monitorozhatjuk. A 3. ábra (a) része a főorsó válaszát (FRF) szemlélteti frekvenciatartományban különböző n fordulatszámokra. Az eredmények alapján megfigyelhető a rendszer f=3,6 kHz körül változó domináns sajátfrekvenciája, mely a fordulatszám növelésével változik. A 3. ábra kinagyított szegmensén (b) látható, hogy az n~0,5–9,0 krpm fordulatszám-tartományban egy domináns módust azonosíthatunk kismértékben növekvő frekvenciával. Az n~9,0–12,0 krpm tartományban 3, majd pedig 2 módus közti átmenet tapasztalható, míg az n~12,0–18,0 krpm közötti fordulatszámoknál egy kb. állandó frekvenciájú módus figyelhető meg. A domináns frekvencia változása mellett ugyancsak azonosítható a rendszer relatív csillapításának nem triviális, 1–6%-os fordulatszámfüggése is (ld. 3. ábra (c)), mely jelentős hatással van a rendszer stabilitási tulajdonságaira [P2].

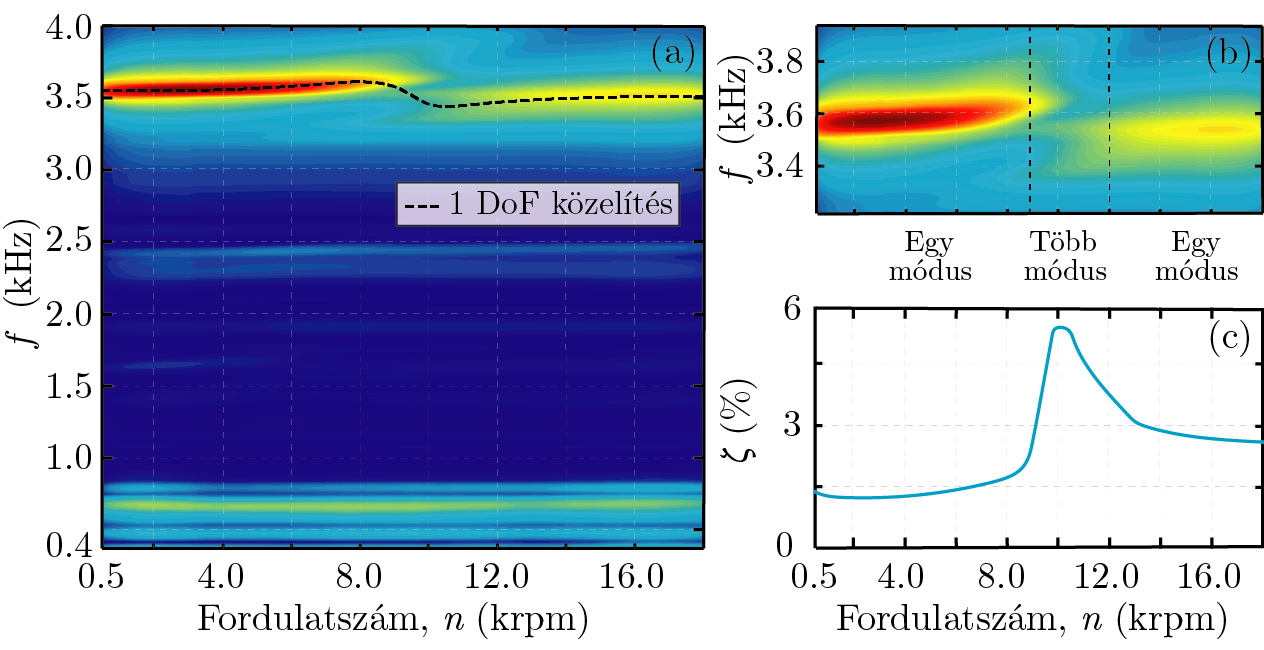
3. ábra: (a) Campbell-diagram (fordulatszámfüggő dinamika). (b) A rendszer domináns frekvenciájának változása. (c) Domináns egy szabadsági fokú (1 DoF) modellhez tartozó relatív csillapítás változása. [P2,P5]

 

Kísérleti és elméleti stabilitásvizsgálat

Kísérleti stabilitásvizsgálat során változtatjuk a főorsó n fordulatszámát, és különböző k₁=0–1,5k virtuális forgácsolóerő-együtthatókra elemezzük a rendszer válaszát, ahol k a főorsó statikus merevsége. A 4. ábra (c) blokkja alapján megfigyelhető, hogy a stabil tartomány (kék határgörbe) alsó burkolója a relatív csillapítás fordulatszámfüggésével azonos változást mutat (ld. 3(c) és 4(a) ábrák). A stabilitási határ mentén ébredő rezgés frekvenciadiagramjának alsó burkolója (ld. 4. ábra (b)) is a 3. ábra (a) részén kimért domináns frekvenciával megegyezően tér el a fordulatszámtól függően.

A rendszer változó dinamikája mellett elvégezhető az emulált anyagleválasztási folyamat elméleti stabilitásvizsgálata is idő- (fekete görbe) és frekvenciatartományban (piros görbe) (ld. 4. ábra alsó blokk), ahol a matematikai leírás az egy szabadsági fokú (1 DoF) csillapított tömeg-rugó lengőrendszer mechanikai modelljét alkalmazza (ld. 2. ábra (a)) [R4]. Az elméleti eredmények jó kvantitatív egyezést mutatnak a mérési eredményekkel. A 4. ábra (c) részén megfigyelhető időtartománybeli vizsgálat (fekete görbe) eltérései az n~9,0–12,0 krpm tartományban tett egy szabadsági fokú közelítéssel magyarázhatók. A frekvenciatartománybeli vizsgálatból adódó stabilitási határ (piros görbe) függőleges irányú eltolódását a mérési eredmények simításából adódó csillapításbeli növekmény okozza.

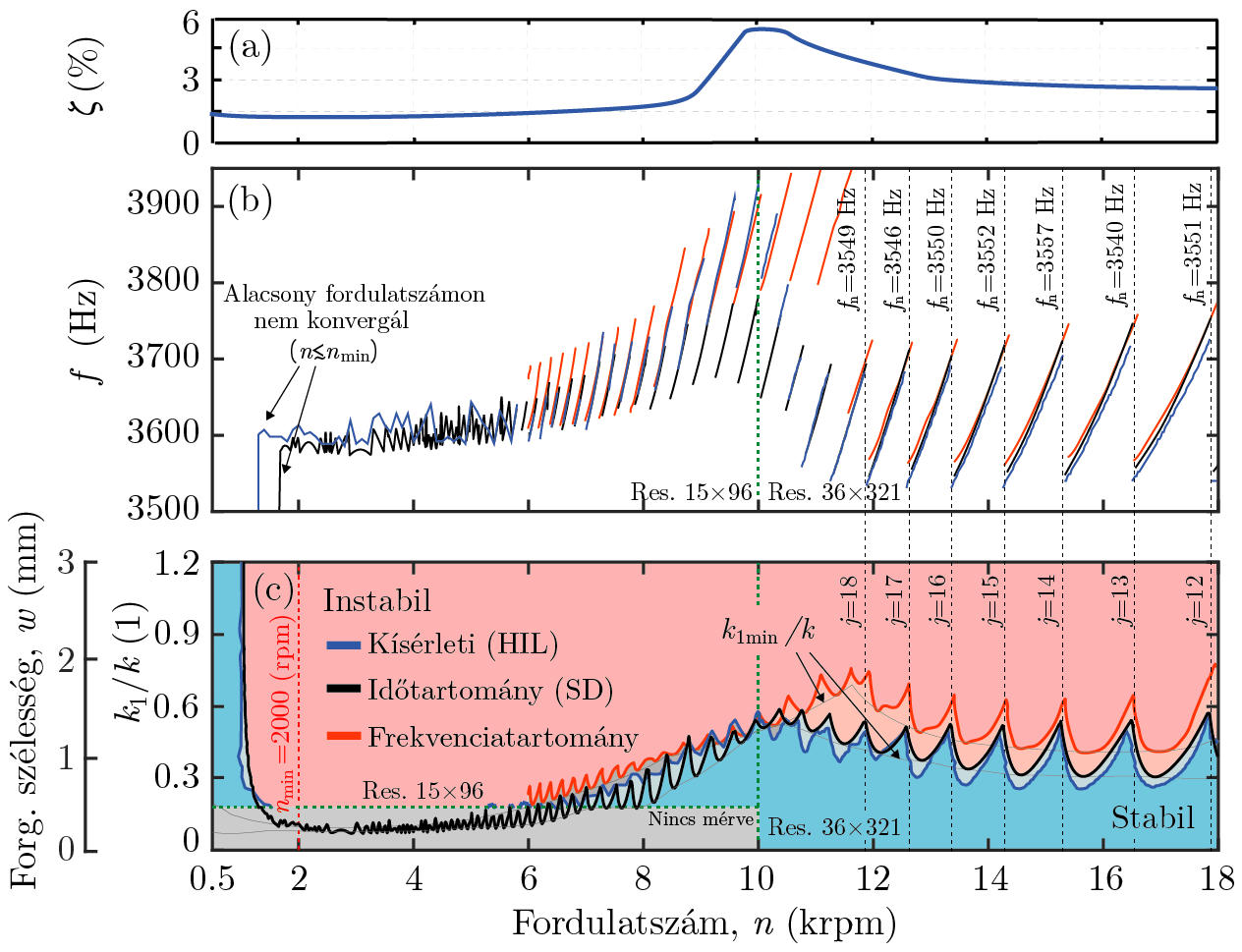
4. ábra: (a) Domináns egy szabadsági fokú (1 DoF) modellhez tartozó relatív csillapítás változása. (b) Stabilitási határon ébredő rezgések frekvencia diagramja. (c) Stabilitási diagram: Környezetszimuláció (HIL, kék) és elmélet (időtartomány - fekete, frekvenciatartomány - piros). [P2]

 

Várható impakt, további kutatás

A kísérleti és elméleti eredmények jól szemléltetik a környezetszimulációs berendezés létjogosultságát. Az emulált folyamat kísérleti stabilitásvizsgálatának előnye, hogy az elméleti modellek bizonytalanságai nélkül, valós szerszámgép-dinamika mellett történik a mérés. Ez alkalmassá teheti a berendezés ipari alkalmazását egy esetlegesen CNC gépekbe beépíthető eszközként, ahol a megmunkálás megkezdése előtt a berendezés stabil paramétertartománya méréssel meghatározható.

 

A kutatás a továbbiakban marási folyamatok vizsgálatára is kiterjed, ahol a szerszámélek geometriájának optimalizálásával tovább javíthatók az anyagleválasztási folyamat stabilitási tulajdonságai. Az így optimalizált szerszámokat költségigényes prototípusgyártás nélkül tudjuk tesztelni.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

Folyóiratcikkek.

[P1] Beri, B., Stepan, G., Essential chaotic dynamics of chatter in turning processes. Chaos, 30, 053108, 2020. (IF: 2,832)

[P2] Stepan, G., Beri, B., Miklos, A., Wohlfart, R., Bachrathy, D., Porempovics, G., Toth, A., Takacs, D., On the stability of emulated turning processes in HIL environment. CIRP Annals, 68(1), 405–408, 2019. (IF: 3,641)

[P3] Beri, B., Stepan, G., Hogan, SJ., Effect of potential energy variation on the natural frequency of an Euler-Bernoulli cantilever beam under lateral force and compression. Journal of Applied Mechanics, 84(5), 051002-1, 2017. (IF: 2,671)

[P4] Beri, B., Hogan, J., Stepan, G., Structural stability of a light rotating beam under combined loads. Acta Mechanica, 228(10), 3735–3740. (IF: 2,102)

[P5] Beri, B., Miklos, A., Takacs, D., Stepan, G., Nonlinearities of hardware-in-the-loop environment affecting turning process emulation. International Journal of Machine Tools and Manufacture. doi.: https://doi.org/10.1016/j.ijmachtools.2020.103611 (In press, IF: 8,019)

 

Konferenciacikkek / Könyvfejezetek.

[C1] Beri, B., Stepan, G., Approximated dynamics of chatter in turning processes. Nonlinear Dynamics of Structures, Systems and Devices, Springer, 463–470, 2020.

[C2] Beri, B., Miklos, A., Takacs, D., Stepan, G., Nonlinearities of emulated turning process in HIL environment. Procedia CIRP (bírálat alatt)

[C3] Beri, B., Stepan, G., Stability of turning process with tool subjected to compression. Procedia CIRP, 77,179–182, 2018.

[C4] Beri, B., Stepan, G., Axiális és torziós terhelés hatása fúrási folyamatok stabilitására, XIII. Magyar Mechanikai Konferencia (MaMek), Augusztus 27–29, 2019, Miskolc, Magyarország.

 

Linkgyűjtemény.

Műszaki Mechanikai Tanszék

SIREN - ERC: Stability Islands: Performance Revolution

 

Hivatkozások listája.

[R1] Miklos, A., Takacs, D., Wohlfart, R., Porempovics, G., Molnar, T.G., Bachrathy, D., Toth, A., Stepan, G., The development of high speed virtual milling test. In: ASME 2017 Dynamic Systems and Control Conference, ASME, New York, DSCC2017 - 5217. ISBN 978-0-7918-5828-8.

[R2] Tobias, SA., Machine Tool Vibrations. Blackie and Son Ltd., London, 1965.

[R3] Tlusty, J., Polacek, M., The stability of machine tools against self-excited vibrations in machining. International Research in Production Engineering, ASME, 1, 465–474, 1963.

[R4] Altintas, Y., Manufacturing Automation. University Press Cambridge, Egyesült Királyság, 2012.

[R5] Altintas, Y., Brecher, C., Weck, M., Witt, S., Virtual Machine Tool. CIRP Annals, 54(2), 115–138, 2005.

[R6] Comak, A., Budak, E., Modeling dynamics and stability of variable pitch and helix milling tools for development of a design method to maximize chatter stability. Precision Engineering, 47, 459–468, 2017.

[R7] Ewins, DJ., Modal Testing: Theory, Practice and Application. Research Studies Press Ltd., Baldock, Hertfordshire, Anglia, 2000.

[R8] Insperger, T., Stepan, G., Semi-Discretization for Time-Delay Systems. Springer Verlag, New York, 2011.