Villamosmérnöki Tudományok  Doktori Iskola 

BME Villamosmérnöki és Informatikai Kar, Automatizálási és Alkalmazott Informatikai Tanszék

Témavezető: Dr. Vajk István

Optimalizálási eljárások alkalmazása mozgástervezési feladatokhoz a robotikában

A kutatási téma néhány soros bemutatása

A robotika napjaink egyik leggyorsabban fejlődő iparága. Életünk számos területén egyre meghatározóbb szerepet játszanak a különböző típusú robotok. Kutatásom során a robotika egyik részproblémájával foglalkozom, amely a mozgástervezéshez kapcsolódik. A mozgástervezés az egyik legalapvetőbb és legfontosabb feladat a robotikában, akár egy önvezető autóról vagy egy ipari szerelőrobotról van szó. A mozgástervezés során a célunk egy ütközésmentes pálya létrehozása adott kezdő- és végpont között. A teljes feladat igen bonyolult, emiatt a problémát gyakran szétcsatoltan oldják meg. Elsőként egy geometriai pályatervező meghatároz egy ütközésmentes pályát, majd a következő fázisban egy sebességprofilt készítünk a már rögzített pályához. Ezt a fázist pályakövetésnek is nevezik az irodalomban. Kutatásom a szétcsatolt mozgástervezés második fázisához kapcsolódik.

A kutatóhely rövid bemutatása

Kutatásomat a BME Automatizálási és Alkalmazott Informatikai Tanszék robotikai csoportjában végzem, Dr. Vajk István témavezetésével. A kutatócsoport elsősorban mobil és ipari robotok navigációjával, irányításával foglalkozik. Az elméleti kutatások mellett, számos pilot projektet is létrehozott a csoport, mint például a 2016-os barcelonai Mobile World Congress-en bemutatott konvojban közlekedő robotautós demonstrációt, vagy a 2019-ben bemutatott VR-szemüveg segítségével irányítható robotautót.

A kutatás történetének, tágabb kontextusának bemutatása

A szétcsatolt mozgástervezés során, a kapott geometriai pálya közvetlenül nem alkalmas a robot irányítására, mivel a pályapontok nem tartalmaznak időkoordinátát [H2]. Ezenkívül a legtöbb esetben a robot bizonyos korlátozásait (pl. dinamikát) nem veszik figyelembe a geometriai tervezők. Emiatt szükséges a szétcsatolt tervezés második fázisa, a sebességprofil-készítés, vagy más néven pályakövetés. A sebességprofil-készítés során többféle célunk is lehet; én az eddigi kutatásaim során időoptimális pályakövetéssel foglalkozom, de léteznek például minimális energiájú eljárások is.

Az időoptimális mozgástervezés fontos szerepet játszik sokféle robotikai alkalmazásban, például űripari feladatoknál, anyagmozgatási problémáknál és számos más ipari folyamatnál is [H3]. Ezekben az alkalmazásokban a minimális idejű algoritmusok növelik a termelékenységet a robot mozgásának optimalizálásával. Néhány esetben pedig a feladatban nem jelenik meg időfüggés, tehát ezek a problémák nem teljesen specifikáltak. Így kihasználható ez az extra szabadságfok a rendszer korlátainak megsértése nélkül.

A kutatás célja, a megválaszolandó kérdések.

Az időoptimális pályakövetés jelenleg is aktív kutatási terület [H4]. A kutatásom célja ezt a kutatási területet kibővíteni olyan megoldásokkal, amelyek az irodalomban található más algoritmusokhoz képest lényegesen gyorsabbak. Az alacsony futási idő elsősorban valós idejű alkalmazások esetén lényeges szempont. Ezenkívül célom, hogy a bemutatott módszerek is képesek legyenek figyelembe venni azokat a korlátokat, amelyeket az irodalomban található alternatív módszerek képesek.

Módszerek

Alapvetően három különböző módszer terjedt el az időben optimális, szétcsatolt mozgástervezési probléma megoldására [H3]. Dinamikus programozás esetén a vizsgált állapotteret felosztjuk egy diszkrét rácson, és az időoptimális megoldást ezen a síkon keressük. Az indirekt módszerek az optimalitás szükséges feltételein alapulnak. Ezzel ellentétben, a direkt módszerek az eredeti probléma egy véges dimenziós közelítését oldják meg. Manapság a direkt megoldások a legalkalmasabbak és legelterjedtebbek az időoptimális sebességprofil-készítés problémájára, főleg valós-idejű alkalmazások esetén [H1,H3].

Az általam kidolgozott módszerek is direkt algoritmusokon alapulnak. A direkt megoldások az eredeti végtelen-dimenziós feladatot átalakítják egy véges problémára, amelyet különböző optimalizálási módszerek segítségével oldanak meg. A direkt módszerek előnye, hogy ezen algoritmusok képesek különböző egyenlőség és egyenlőtlenség típusú korlátozásokat is figyelembe venni, valamint a feladatleírásban megjelenő paraméterváltozásokat is könnyedén kezelik.

A direkt módszerek alapvetően optimalizálási módszereken alapulnak. A matematikai optimalizálás esetén a feladat az, hogy a vektorok egy megengedett halmazából kiválasszuk a legjobb vektort (a jóságot egy függvény segítségével írjuk le). A konvex optimalizálás az egyik legnépszerűbb optimalizálási módszer, amelyet gyakran alkalmaznak, a szabályozástechnikától, egészen a pénzügyi problémákig. Az időoptimális pályakövetési feladat esetén is alkalmazható a konvex optimalizálás, mivel a feladat leírható egy másodrendű konvex program (SOCP) segítségével [H3].

Kutatásom során az SOCP-feladatból indultam ki, és ehhez kapcsolódóan kidolgoztam egy új optimalizálási módszert, a csúcsos feladatleírást [F4,F5]. Egy nemlineáris program, szigorúan monoton csökkenő célfüggvény és speciális korlátozások (csúcsos tartomány) mellett gyorsabban megoldható, mint az eredeti feladat. Az 1. ábrán látható egy egyszerű csúcsos tartomány. Habár az irodalomban található SOCP-pályakövetési feladat megengedett tartománya nem csúcsos, kidolgoztam viszont egy alternatív diszkretizálási módszert, amely segítségével csúcsos feladatot kapunk [F2]. A csúcsos leírásnak köszönhetően a másodrendű, SOCP-feladat egy lineáris, LP-feladat segítségével megoldható. Az LP-feladat előnye a lényegesen alacsonyabb számítási igény.

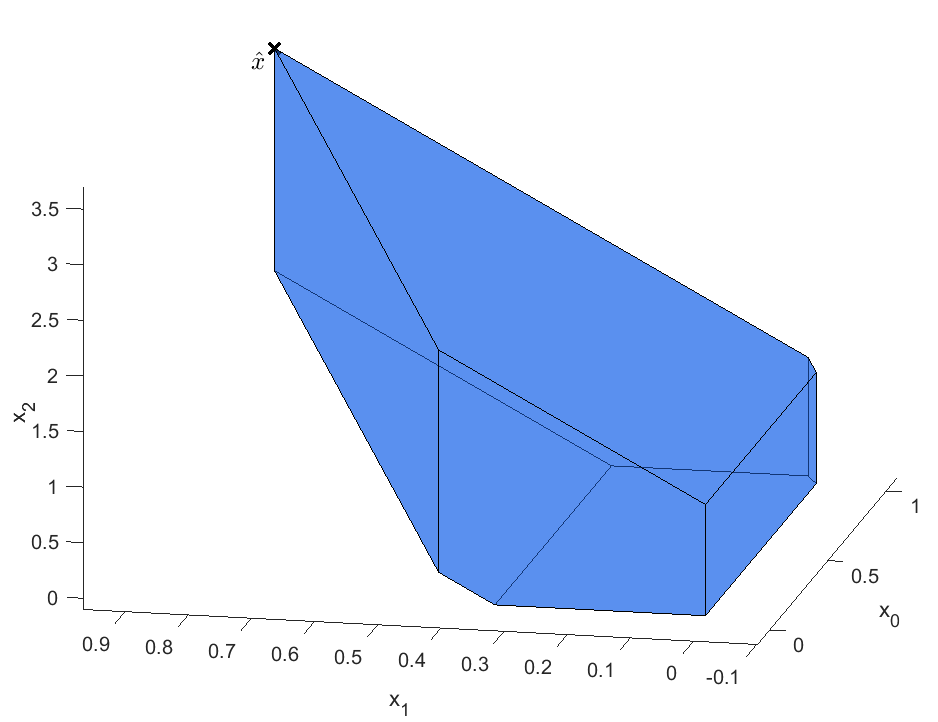
1. ábra: Egy egyszerű háromdimenziós csúcsos tartomány.

Az LP-feladatleírás már önmagában közel egy nagyságrenddel gyorsítja a pályakövetési probléma megoldását az irodalomban eddig található módszerekhez képest. A feladat ritka, sávos felépítését kihasználva azonban további gyorsítást tudunk elérni. Ennek érdekében kidolgoztam egy szekvenciális algoritmust ritka, csúcsos feladatok megoldására [F4,F5]. A mérési eredmények alapján, a szekvenciális metódus további két nagyságrenddel gyorsítja a feladat megoldását.

Bizonyos korlátok esetén nem tudjuk használni a konvex optimalizálási eszközöket az időoptimális pályakövetésnél, mivel ezek a korlátozások nem írhatók le konvex függvények segítségével. Ebbe a csoportba tartozik például a viszkózus súrlódás vagy a robot csuklóinak nyomaték-sebesség karakterisztikája. Általánosságban, ilyenkor nemkonvex eljárásokat tudunk alkalmazni, viszont ezek esetén a számítási idő lényegesen magasabb. Azért, hogy ezeket a korlátokat is kezelni tudjuk valós idejű alkalmazások esetén, kidolgoztam egy megoldási módszert a problémára [F1,F3]. A megoldás biztosítja, hogy ezen problémák lokális szélsőértéke egyben globális szélsőérték is legyen, ezáltal lényegesen gyorsítva a feladat megoldását.

Eddigi eredmények

Az előző fejezetben tárgyalt új optimalizálási módszerek segítségével az időoptimális pályakövetési feladat lényegesen gyorsabban megoldható. A vizsgált módszerek számítási igénye a pálya hosszának függvényében a 2. ábrán látható. Megállapítható, hogy a bemutatott szekvenciális algoritmus közel két nagyságrenddel gyorsabban megoldja a feladatot, mint a második Gurobi LP-eljárás. A Gurobi az egyik legkorszerűbb optimalizációs eszköz, amelyet sok cég (pl. Google, Toyota, Microsoft) és kutatóintézet használ. Az ábrán szerepel az úgynevezett MTSOS-algoritmus is. Az MTSOS-eljárást Thomas Lipp készítette az időoptimális pályakövetési feladatokhoz 2014-ben, aki a Stephen Boyd által vezetett laboratórium kutatója a Stanford Egyetemen.

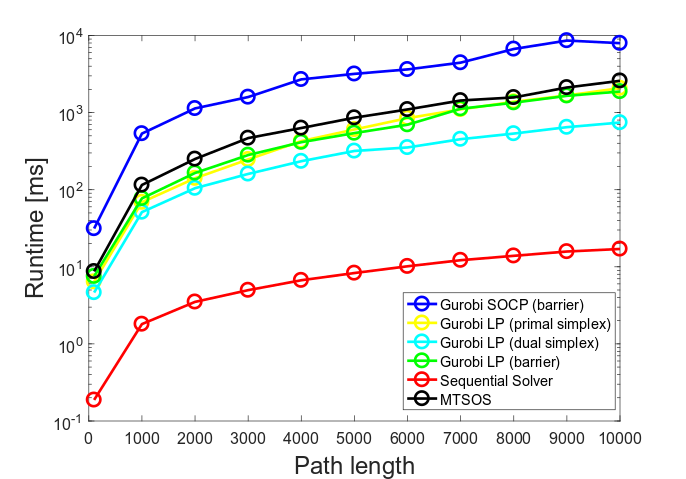
2. ábra: Különböző algoritmusok futási ideje a rögzített pálya méretének függvényében.

A bemutatott módszerekről több publikáció is készült rangos folyóiratokban [F1-F5], emellett a gyakorlatban is kipróbáltuk a módszereket a tanszéki hat szabadságfokú robotkar segítségével. Az egyik esetben az úgynevezett pincérproblémát (waiter motion problem) oldottuk meg a robotkarral (lásd 3. ábra). A feladat lényege egy tálca mozgatása, amelyen egy vagy több pohár található. A cél, hogy a lehető legrövidebb idő alatt végezzük el a mozgást az előre meghatározott pályán, és közben a pohár ne csússzon le a tálcáról. Egy hasonló, ipari probléma a pick-and-place feladat, amely például logisztikai alkalmazásokban fontos.

3. ábra: A pincérprobléma megoldása a tanszéken található robotkar segítségével.

Szintén a bemutatott kutatáshoz tartozik egy másik gyakorlati alkalmazás, amely egy japán robotikai vállalathoz köthető. A vállalat elsősorban látórendszereket fejleszt ipari robotokhoz. Ezeket a rendszereket számos gyárban alkalmazzák a világ minden táján. A szekvenciális algoritmus alapján készítettünk számunkra egy exkluzív szoftvert az időoptimális pályakövetési feladat megoldására. A szoftver képes együttműködni a Robot Operating System (ROS) platformmal, amely igen népszerű robotikai termékekben és akadémiai fejlesztésekben egyaránt. Az általunk készített program sokféle korlátozást képes kezelni, beleértve a robot megfogó egységére és a csuklókra vonatkozó korlátokat. A 4. ábrán látható egy példa, ahol a mozgáshoz tartozó sebességprofil a bemutatott szekvenciális algoritmussal készült. A szoftverkészítés a BME és a vállalat közötti szerződéses együttműködés alapján történt (szerződés száma: AUT 2019, 411.175/2019).

4. ábra: A japán robotikai vállalat egyik megoldása, amely során a robot pick-and-place feladatot végez egy látórendszer segítségével. A megoldás során alkalmazott sebességprofilt a szekvenciális eljárással készítik.

Várható impakt, további kutatás

Az időben optimális mozgástervezés, és ezen belül is a sebességprofil-készítés még ma is aktív kutatási terület. Ezt mutatja, hogy a közelmúltban is számos publikáció született a témában [H4]. Az év elején jelent meg egy közös cikkünk a Pármai Egyetem kutatóival, amelyben továbbfejlesztettük a bemutatott szekvenciális algoritmust [F5]. Ehhez a cikkhez kapcsolódóan pedig a Massachusettsi Műszaki Egyetem kutatói további elméleti eredményeket mutattak be [H6].

Mivel a szekvenciális eljárás akár 1 ms alatt képes megadni az adott pályához tartozó bejárási időt, így az algoritmust a geometriai pályatervezéshez is felhasználnám a jövőben. Az eddig tárgyalt megközelítésben a mozgástervezés két fázisa teljes mértékben szétválik. Egy kis számítási igényű pályakövetési algoritmus viszont meg tudná adni az adott pályához tartozó bejárási időt, így ez alapján a geometriai tervező választani tudna a felmerülő pályák közül. Ez mindenképp nagy előrelépés lenne, hiszen a jelenlegi megközelítésben a geometriai pályát rögzítettnek tekintjük.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó folyóiratcikkek:

[F1] Á. Nagy, G. Csorvási, I. Vajk. “Path Tracking Algorithms for Non-Convex Waiter Motion Problem”. In: Periodica Polytechnica Electrical Engineering and Computer Science 62.1 (2018), pp. 16–23.

[F2] Á. Nagy, I. Vajk. “LP-based velocity profile generation for robotic manipulators”. In: International Journal of Control 91.3 (2018). IF*: 2.101, pp. 582–592.

[F3] Á. Nagy, I. Vajk. “Non-Convex Time-Optimal Trajectory Planning for Robot Manipulators”. In: Journal of Dynamic Systems, Measurement, and Control (2019). IF*: 1.521, megjelenés alatt

[F4] Á. Nagy, I. Vajk. “Sequential Time-Optimal Path Tracking Algorithm for Robots”. In: IEEE Transactions on Robotics (2019). IF*: 4.264. megjelenés alatt

[F5] L. Consolini, M. Locatelli, A. Minari, Á. Nagy, I. Vajk. “Optimal Time Complexity Speed Planning for Robot Manipulators”. In: IEEE Transactions on Robotics 35.3 (2019). IF*: 4.264, pp. 790–797.

Kapcsolódó konferenciacikkek:

[K1] Á. Nagy, I. Vajk. “Validating Time Optimal Path Tracking Algorithm for Robots”. In: Proceedings of the Automation and Applied Computer Science Workshop 2016: AACS’16. 2016, pp. 141–149.

[K2] Á. Nagy, I. Vajk. “Minimum-time path tracking for robots with nonconvex constraints”. In: 2017 IEEE 15th International Symposium on Intelligent Systems and Informatics (SISY). 2017, pp. 163–168.

[K3] Á. Nagy, I. Vajk. “Peaked Optimisation Problem for Motion Planning in Robotics”. In: Proceedings of the Automation and Applied Computer Science Workshop 2017: AACS’17. 2017, pp. 147–156.

[K4] G. Csorvási, Á. Nagy, I. Vajk. “Near Time-Optimal Path Tracking Method for Waiter Motion Problem”. In: 20th World Congress of the International Federation of Automatic Control. 2017, pp. 4929–4934.

Hivatkozások listája:

[H1] Thomas Lipp, Stephen Boyd. “Minimum-time speed optimisation over a fixed path”. In: International Journal of Control 87.6 (2014), pp. 1297–1311.

[H2] B. Siciliano, O. Khatib. “Springer Handbook of Robotics”. Springer-Verlag Berlin Heidelberg, 2008.

[H3] D. Verscheure, B. Demeulenaere, J. Swevers, J. Schutter, M. Diehl. “Time-Optimal Path Tracking for Robots: A Convex Optimization Approach”. In: IEEE Transactions on Automatic Control 54.10 (2009), pp. 2318–2327.

[H4] H. Pham, Q. Pham. “A New Approach to Time-Optimal Path Parameterization Based on Reachability Analysis”. In: IEEE Transactions on Robotics 34.3 (2018), pp. 645–659.

[H5] F. Debrouwere, W. Van Loock, G. Pipeleers, Q. T. Dinh, M. Diehl, J. Schutter, J. Swevers. “Time-Optimal Path Following for Robots with Convex-Concave Constraints Using Sequential Convex Programming”. In: IEEE Transactions on Robotics 29.6 (2013), pp. 1485-1495.

[H6] I. Spasojevic, V. Murali, S. Karaman. “Asymptotic Optimality of a Time Optimal Path Parametrization Algorithm”. Version 1. 2019. arXiv: 1904.04968 [cs.RO]