Matematika- és Számítástudományok Doktori Iskola  

BME Természettudományi Kar, Geometria Tanszék

Témavezető: Dr. Szirmai Jenő

Szabályos horoszféra kitöltések a hiperbolikus terekben

A kutatási téma néhány soros bemutatása

Vizsgálataim az állandó negatív görbületű Bolyai-Lobacsevszkij féle hiperbolikus térhez kapcsolódnak, melynek születését a magyar matematikának is köszönhetjük: „...semmiből ujj más világot teremtettem” írta Bolyai János apjának címzett levelében 1823. november 3-án. Témám, mint látni fogjuk, több szálon kapcsolódik a magyar matematikatörténethez. Az optimális gömbkitöltések problémája annak vizsgálata, hogy egy adott térben hogyan lehet egybevágó gömböket átfedés nélkül úgy elhelyezni, hogy a lehető legnagyobb sűrűségű elrendezést kapjuk.

 

Kutatásomban a hiperbolikus tér egybevágó gömbkitöltéseivel, azon belül a legjobbnak bizonyuló ún. horoszférikus gömbök segítségével találtam az eddig ismert legsűrűbb gömbkitöltéseket n=3,...,9 dimenziókban.

 

Kutatóhely rövid bemutatása

Munkámat a BME, Matematika Intézet, Geometria Tanszéken végzem, dr. habil. Szirmai Jenő témavezetésével a Nemeuklideszi Geometriák Kutatócsoport tagjaként. A Geometria Tanszék, mint a Strommer Gyula által alapított Ábrázoló Geometria Tanszék örököse, a geometriához kapcsolódó kutatások széles spektrumát végzi a fizika geometriai vonatkozásaitól kezdve az euklideszi és nemeuklideszi diszkrét geometriák sokrétű vizsgálatáig.

 

Kutatás történetének, tágabb kontextusának bemutatása

 A Thurston-féle geometrizációs tétel szerint Világegyetemünk geometriájának leírásában alapvetően nyolc geometria fordulhat elő. Ezek a maximális homogén Riemann-geometriák az ún. Thurston-geometriák, köztük szerepel a három állandó görbületű tér, az euklideszi, gömbi és hiperbolikus geometria, de találhatók más egzotikusabb terek is. Így mind a nyolc geometriában érdekes vizsgálni, hogy a kristályos anyagok szerkezete milyen lehet, azaz az atomok elhelyezkedése milyen rendszerben történhet. Ezen kérdéskörben általában az atomokat gömbökkel modellezzük, és azt vizsgáljuk, hogy az adott térben milyen elhelyezkedések lehetségesek. Érdekes az egyes terek diszkrét egybevágóság-csoportjainak feltérképezése, melyek leírják a tér szimmetriáit. Euklideszi térben 230 ilyen kristálycsoport lehetséges melyek gömbkitöltéseit alaposan megvizsgálták. További Thurston-geometriák esetében azonban sok a nyitott kérdés, nem beszélve a magasabb dimenziós hiperbolikus terekről [Sz07, Sz13].

 

Tekintsük a témakör két friss nevezetes eredményét:
 

• A történelmi kiindulópont euklideszi térben Kepler nevéhez fűződik, aki 1611-ben fogalmazta meg híres sejtését, miszerint 3 dimenzióban a legsűrűbb kongruens gömbök elrendeződése 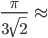 74% körüli sűrűségű. Ezen sejtést viszont csak nemrég, 1998-ban sikerült igazolnia Thomas Halesnek, Fejes-Tóth László eredményeinek felhasználásával, a ma rendelkezésre álló számítógépes háttér segítségével [H].

 

• Egy másik friss nevezetes eredmény az, hogy 8 dimenziós euklideszi térben a legsűrűbb gömbkitöltés az 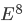rács segítségével realizálódik [V], melyet Viazovska 2016-ban bizonyított.
  
  A gömbkitöltések egyik kiemelt alkalmazása a számítástechnika területén a hibajavító kódok elmélete. Egy csatornán áthaladó jelsorozatba redundanciákat építenek; ehhez szükséges a jelek közötti távolság optimalizálása, melyeket jelek körüli “gömbökkel” modelleznek.

  

Kutatás célja, megválaszolandó kérdések

A hiperbolikus térben a gömböknek három típusa létezik: klasszikus gömb, horoszféra, és hiperszféra. Kutatásomban én horoszférakitöltésekkel foglalkozom. Választásomat az indokolja, hogy a 2 és 3 dimenziós esetekben a legsűrűbb gömbkitöltés elrendezések ezen gömbtípussal realizálódnak (2 dimenzióban Fejes Tóth László [FTL], 3 dimenzióban id. Böröczky és Florian [BF] eredményei alapján). A sűrűség fogalmát hiperbolikus terekben a kitöltés Dirichlet-Voronoi cella rendszeréhez viszonyítjuk, mely cellák egyben a szimmetriacsoportok alaptartományai is [FKK].

 

A hiperbolikus térben adott r sugarú gömbökkel az id. Böröczky Károly-féle szimpliciális sűrűség felső korlátja szerint lokálisan a legsűrűbb gömbkitöltést úgy érjük el, ha egy 2r élhosszúságú szabályos szimplex csúcsaiba helyezzük a gömbök középpontjait [B,K98]. (Egy szimplex n dimenzióban n+1 általános helyzetű pont konvex burka.) Szimpliciális sűrűségnek nevezzük az előbbi gömböknek a szimplexbe eső térfogatainak és a szimplex térfogatának a hányadosát. A 3 dimenziós hiperbolikus térben ismert monotonitás tétel szerint a sugár függvényében növekszik a szimpliciális sűrűség függvény; ezt jelölje , ahol ez esetben n=3. (Megjegyezzük, hogy ezt a jelenséget a negatív görbület okozza, az euklideszi térben a sugártól független e sűrűség.) Ezen monotonitás alapján 3 dimenzióban bizonyították, hogy a legsűrűbb gömbkitöltés határesetben a hiperbolikus tér határán lévő középpontú gömbökkel, ún. horoszférákkal realizálódik, amelyek középpontjai a hiperbolikus tér modelljének határáig nyúló szabályos aszimptotikus tetraédert feszítenek ki, lásd 1.(a) ábra. A hiperbolikus 3 dimenziós térben meglepő módon ez az aszimptotikus tetraéder kövezi a teret. Így ez a sűrűség a felső korlát, mely 85.3% körüli értékeket ad, gömbkitöltésként megvalósul, ha nem is klasszikus gömbökkel, hanem horoszférákkal [BF]. Ezt a kitöltést a Cayley-Klein gömbmodellben az 1.(b) ábra szemlélteti. 

             

                               (a)                                                                          (b)

 

1. ábra: Böröczky-féle optimális gömbkitöltés a 3 dimenziós hiperbolikus tér gömbmodelljében. (a) Négy egybevágó horoszféra a tetraéder (szimplex) alaptartományában. (b) Az alaptartomány oldalaira vonatkozó tükrözéssel kapott gömbkitöltés.

 

A hiperbolikus térben minden horoszféra egybevágó, azaz létezik egy bármely horoszférát bármely másikba átképző egybevágósági transzformáció. A korábbi munkáinkban bevezetett szabályos gömbkitöltés cellarendszeréhez viszonyítva a különböző típusú, de kongruens horoszférákkal történő kitöltések új lehetőségeket nyitottak a gömbkitöltések vizsgálatában, mint ahogy azt a 2000-es években a Geometria Tanszéken témavezetőm megmutatta [Sz12]. Fontos kérdéssé vált az aszimptotikus csúcsokkal rendelkező Coxeter-kövezésekhez tartozó horoszférakitöltések áttekintése, mivel sejtettük, hogy ezek nagyon sűrű gömbkitöltéseket fognak adni. Ilyen aszimptotikus Coxeter-kövezések (melyet Koszul-féle kövezéseknek is neveznek) n=2,...,9 dimenzióig léteznek és n≥3 esetén csak véges sokan vannak és térfogatuk ismert [JKRT,JKRT2]. Eddigi vizsgálatainkban sok új pozitív eredményre jutottunk, mind a 3-tól 9 dimenziós esetekig.

 

Módszerek

A kutatási módszerünk két pilléren nyugszik. Az egyik a hiperbolikus geometria projektív modelljének apparátusa, amelyet az általunk kifejlesztett tételekkel alkalmassá tettünk gömbkitöltések elemzésére [Mo]. A másik pillér az általunk kifejlesztett számítógépes program, amellyel számolni tudjuk a gömbkitöltések sűrűségeit. Mindezekhez a Mathematica programcsomagokat használjuk, amelyek numerikus és szimbolikus számításokat tesznek lehetővé.

 

A kutatások elvégzéséhez a szakirodalom feldolgozása mellett számítógépes támogatásra is szükség van. Ezzel lehetővé válnak a bonyolult számítások egyszerűsítései, illetve az elméletben meghatározott konfigurációk vizualizálása 3 dimenzióban.

 

A témakör klasszikus eredményei többek között Fejes Tóth László és id. Böröczky K. munkásságából származtathatóak. Id. Böröczky bizonyította, hogy hiperbolikus térben a sűrűségek a tér cellarendszerekre való felbontásától függnek [FKK]. Ez a kérdéskör kapcsolódik a Banach-Tarszki paradoxonhoz, mely szerint a probléma átdarabolhatósági okokra vezethető vissza. Munkánkban a probléma megoldásához a gömbkitöltés sűrűségszámítási módszerét a Dirichlet-Voronoi cellarendszerhez kapcsoljuk.

 

Fejes-Tóth L. és H.S.M Coxeter sejtették, hogy a legsűrűbb r sugarú gömbökkel történő gömbkitöltéseknél a gömbök középpontjai mindig szabályos szimplexek csúcspontjaihoz tartoznak. Két dimenzióban Fejes-Tóth L. bizonyította a sejtést, majd a 1964-ben Böröczky K. és Florian A. bizonyította a teljesen aszimptotikus szimplex kövezés optimalitását 3 dimenziós hiperbolikus térben [BF].

Észrevételünkben azáltal, hogy „különböző típusú” horoszférakitöltéseket is vizsgáltunk, a korábbi bizonyítás néhány hiányosságára is rámutattunk. Az általunk alkalmazott módszerrel minden lehetséges aszimptotikus Coxeter szimplexhez tartozó horoszférakitöltést megvizsgáltunk.

 

Eddigi eredmények

Fő eredményünk, hogy minden dimenzióban, ahol aszimptotikus Coxeter-kövezések találhatók,  dimenzió esetén sikerült megtalálnunk az eddig ismeretlen legsűrűbb gömbkitöltést, illetve  esetén a bizonyítottan optimálissal megegyező sűrűségű új gömbkitöltést a horoszférák segítségével. Kiemeljük továbbá, hogy  dimenzióban sikerült megcáfolni, sőt túllépni, Fejes Tóth László az optimális gömbkitöltés sűrűségére vonatkozó  értékű sejtését.

 

A következő táblázatban röviden összefoglaljuk eredményeinket. A felső elméleti korlátot az említett  szimpliciális sűrűségfüggvény adja, amelyhez tartozó kövezés nem realizálható, pedig a korlát és az általunk realizált sűrűségi értékek különbsége.

 

 

3 dimenziós hiperbolikus tér

 

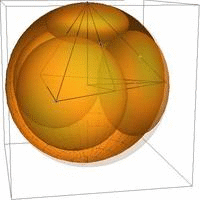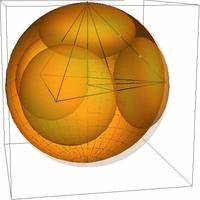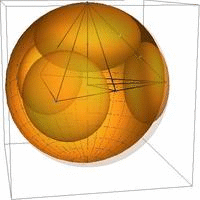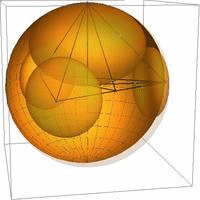
Kiemelt fontosságú eredményünk 3 dimenzióban a Böröczky-féle felső korláttal megegyező, de a klasszikusan ismert kitöltéstől eltérő konfigurációjú és szimmetriájú horoszférakitöltések létezésének igazolása. Ezen kitöltések tárgyalásához használjuk a horoszfératípus fogalmát, melyet a gömbkitöltést alkotó horoszférák alaptartományához viszonyított relatív sűrűsége jellemez. A 2.(a) ábra különböző lehetséges szabályos aszimptotikus szimplex (tetraéder) alaptartományhoz viszonyított horoszfératípusokat szemlélteti [Sz05,KSz1,KSz3,KSz4], a 2.(b-c) pedig az általunk talált új optimális szélső esetet.

                  

(a)	(b)	(c)

                                                                              

2. ábra: (a) Átmenet Böröczky-féle optimális gömbkitöltésből (alapeset) a mi új megegyező sűrűségű konfigurációnkba (végső eset), (b) a tetraéder-kövezéshez tartozó általunk talált új optimális horoszféra kitöltés két horoszféra típussal az alaptartományban, (c) tükrözésekkel kiterjesztett térben.

 

 

4 dimenziós hiperbolikus tér

Hasonló módon, 4 dimenzióban is találtunk az aszimptotikus Coxeter szimplex kövezésekhez tartozó gömbkitöltéseknek egy olyan osztályát, melynek tagjai meghaladják Fejes-Tóth Lászlónak témában alapnak számító 1964-es könyvében [FTL] megfogalmazott 0,690... értékű felső sűrűség korlátra vonatkozó sejtését 0,71644896… értékekkel [KSz2].

 

 

5 dimenziós hiperbolikus tér

5 dimenzióban, hasonlóan a 12 aszimptotikus Coxeter szimplexek horoszférakitöltéseinek vizsgálatához, újabb alsó korlátot adtunk, és az optimális sűrűséget  közötti értékekre korlátoztuk (3. Ábra) [KSz5].

 

 

 

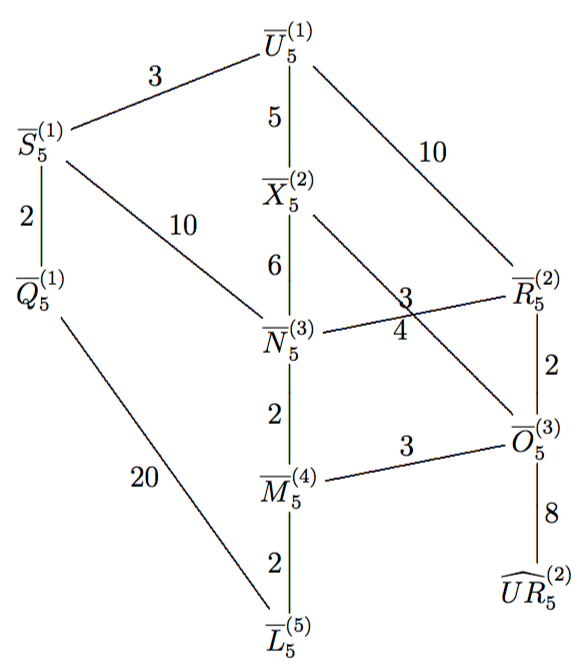
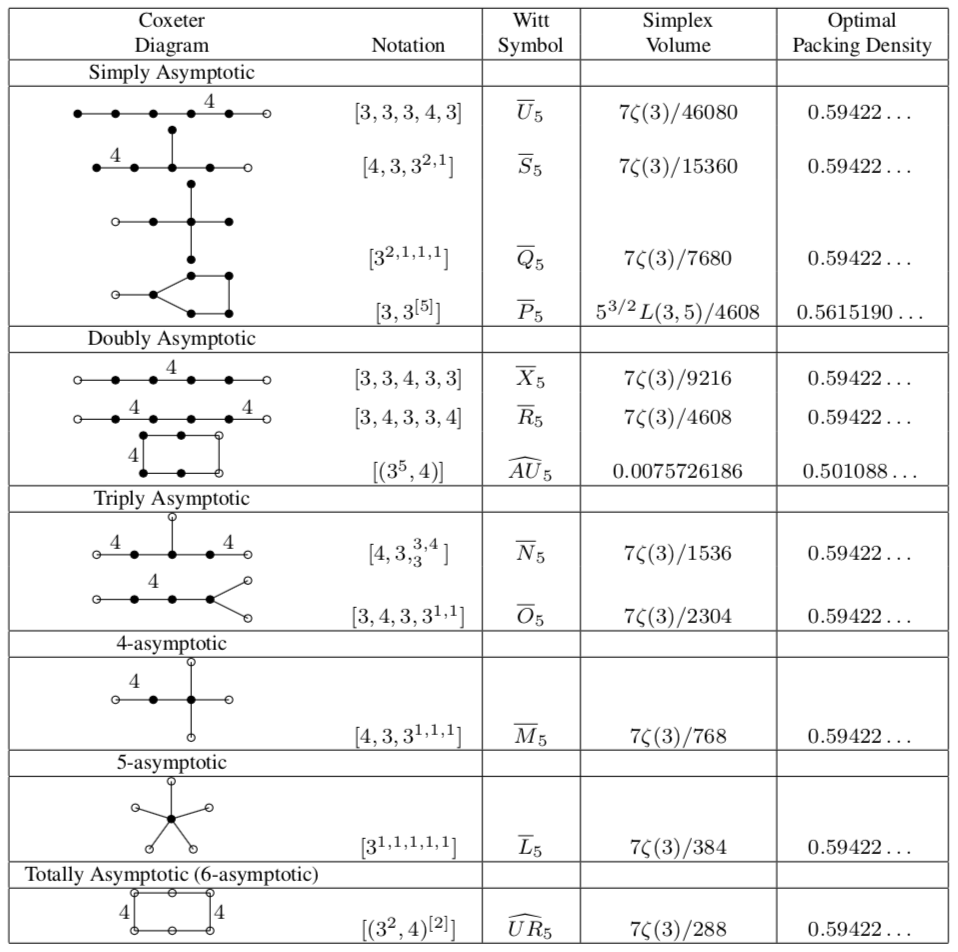
3. Ábra: Coxeter szimplex szimmetriák részcsoport diagramja;

 12 alaptartomány adatait (sűrűségek, térfogatok a Riemann-féle zéta-függvényben).

 

6-9 dimenziós hiperbolikus tér

Ezen esetek vizsgálata [KSz6] az Emberi Erőforrások Minisztériuma ÚNKP-18-3 kódszámú Új Nemzeti Kiválóság Programjának támogatásával készült. Ezekről az esetekről a bevezetőben szereplő összefoglaló táblázatból, valamint a következő előadás videóból tájékozódhat.

  

Várható impakt, további kutatás

Eredményeinket nemzetközi folyóiratokban és konferenciákon közöltük. Előadtunk az MTA Rényi Alfréd Matematikai Kutatóintézetben Fejes Tóth László 100., illetve Bárány Imre akadémikus 70. születésnapja alkalmából szervezett konferenciákon [K1], a BME-n megrendezett Discrete Geometry Days 2016 és 2019 konferenciákon, külföldön pedig a Berlin Mathematical School Discrete and Convex Geometry Nyári Iskolán, valamint a Bécsi Műszaki Egyetemen szervezett Szimmetria Fesztiválon. Kiemelt publikációk jelentek meg a Discrete and Computational Geometry, valamint Monatshefte für Mathematik folyóiratokban. Független hivatkozás született a matematikai csomóelméleti alkalmazásról vezető folyóiratban [C]. Munkánkra a Wikipédiában is hivatkoznak.

 

Későbbi terveinkben további hasonló Thurston-geometriai kutatások szerepelnek. A dinamikai rendszerekkel való kapcsolatot aritmetikus valamit Klein-csoportokon keresztül fejlesztjük tovább[KD].

 

Saját publikációk

[K1] Kozma, R.T., Dense regular horoball packings in higher dimensional hyperbolic spaces, Discrete Geometry and Convexity in honour of Imre Bárány, Eds. Ambrus G., Böröczky K.J., Füredi Z., pp. 143-144, Budapest, Hungary (2017). ISBN 978-963-279-963-6

 

[KSz1] Kozma R. T., Szirmai J. Symmetries of Horoball Packings Related to Famous 3-dimensional Hyperbolic Tilings, Symmetry: Culture and Science, Volume 27, No. 4, pp 261-278 (2016).

 

 [KSz2] Kozma R. T., Szirmai J. New Lower Bound for the Optimal Ball Packing Density in Hyperbolic 4-space, Journal of Discrete and Computational Geometry, Volume 53, Issue 1, pp 182-198 (2015).

 

 [KD] Kozma, R. T., Devaney, R. L. Julia Sets Converging to Filled Quadratic Julia Sets, Journal of Ergodic Theory and Dynamical Systems, Volume 34, Issue 01, pp. 171-184 (2014).

 

[KSz3] Kozma, R. T., Szirmai J. Optimally Dense Packings for Fully Asymptotic Coxeter Tilings by Horoballs of Different Types, Monatshefte für Mathematik, Volume 168, Issue 1, pp. 27-47 (2012)

 

[KSz4] Kozma, R. T., Szirmai J., Structure and Visualization of Optimal Horoball Packings in 3-dimensional Hyperbolic Space, ArXiv:1601.03620. (Benyújtott kézirat)

 

[KSz5] Kozma, R.T., Szirmai J., New Horoball Packing Density Lower Bound in Hyperbolic 5-space. (Megjelenés alatt, Geometriae Dedicata)

[KSz6] Kozma, R.T., Szirmai J., Optimal Horoball Packing Densities for Coxeter Simplex Tilings in Hyperbolic n-space for n=6,7,8,9.  (Kézirat)

Linkgyűjtemény

BME Matematika Intézet

BME Geometria Tanszék

dr. habil. Szimai Jenő honlapja

Saját honlap képekkel és Mathematica kóddal

Angol nyelvű Wikipedia honlap gömb kitöltésekről eredményeink említésével

Wolfram Demonstrations Project honlapján publikált Vizualizáció

 

Hivatkozások listája

[B] Böröczky,K. Packing of spheres in spaces of constant curvature, Acta Math. Acad. Sci. Hungar., 32 (1978), 243–261.

[BF] Böröczky, K. Florian, A. Überdiedichteste Kugelpackung im hyperbolischen Raum, Acta Math. Acad. Sci. Hungar., 15 (1964), 237–245.

[C] Adams, Colin, et al. Densities of hyperbolic cusp invariants of knots and links. Proc. Amer. Math. Soc. (2018).

[H] Hales, T. C. Historical Overview of the Kepler Conjecture, Discrete and Computational Geometry, 35 (2006), 5–20.

[FKK] Fejes Tóth, G. Kuperberg, W. Kuperberg, Packing and Covering with Convex Sets, Handbook of Convex Geometry, Volume B, eds. Gruber, P.M., Willis J.M., pp. 799-860, North- Holland, (1983).

[FTL] Fejes Tóth, L. Regular Figures, Macmillian (New York), 1964.

[JKRT] Johnson, N.W., Kellerhals, R., Ratcliffe, J.G., Tschants, S.T. The Size of a Hyperbolic Coxeter Simplex, Transformation Groups, 4/4 (1999), 329–353.

[JKRT2] Johnson, N.W., Kellerhals, R., Ratcliffe, J.G., Tschants, S.T. Commensurability classes of hyperbolic Coxeter Groups, Linear Algebra and its Applications, 345 (2002), 119–147.

[K98] Kellerhals, R. Ball packings in spaces of constant curvature and the simplicial density function, Journal für reine und angewandte Mathematik, 494 (1998), 189– 203.

[Mo] Molnár, E. The Projective Interpretation of the eight 3-dimensional homogeneous geometries, Beitr. Algebra Geom., 38/2 (1997), 261–288.

[Sz05] Szirmai, J. The optimal ball and horoball packings of the Coxeter tilings in the hyperbolic 3-space Beitr. Algebra Geom., 46/2 (2005), 545–558.

[Sz07] Szirmai, J. The optimal ball and horoball packings to the Coxeter honeycombs in the hyperbolic d-space Beitr. Algebra Geom., 48/1 (2007), 35–47.

[Sz12] Szirmai, J. Horoball packings and their densities by generalized simplicial density function in the hyperbolic space, Acta Math. Hung., 136/1-2 (2012), 39–55, DOI: 10.1007/s10474-012-0205-8.               

[Sz13] Szirmai, J. Horoball packings to the totally asymptotic regular simplex in the hyperbolic n-space, Aequationes Mathematicae, 85 (2013), 471-482, DOI: 10.1007/s00010-012-0158-6.

[V] Viazovska, M. S. "The sphere packing problem in dimension 8." Annals of Mathematics 185, no. 3 (2017): 991-1015.