Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Hidrodinamikai Rendszerek Tanszék

Témavezető: Dr. Hegedűs Ferenc

Harmonikusan gerjesztett buborék dinamikai vizsgálata nagy viszkozitású folyadékban

A kutatási téma néhány soros bemutatása

Folyadékok ultrahanggal történő besugárzása a kémia egy új, nagy lehetőségeket ígérő módszere. Fizikai alapját a kavitáció egy speciális esete, az akusztikus kavitáció adja. Az ultrahangos besugárzás hatására a folyadékban több ezer, mikron méretű buborék keletkezik, amelyek radiális pulzálást végeznek. A radiálisan pulzáló buborékok összeroppanása olyan erős lehet, hogy a buborékok belsejében a hőmérséklet elérheti a több ezer Kelvin fokot is [1], ami kedvez a kémia reakciók lejátszódásának (szonokémia [2]). Ezzel egyes kémiai folyamatok hatékonyságát jelentősen növelni lehet, ami forradalmasíthatja a hagyományos vegyipari eljárásokat. Egy innovatív áttörés a vegyipar bővülését eredményezheti, amely jelenleg az ipari termelés 8,6%-át teszi ki. Ez hozzájárulhat a magyarországi autóipar túlsúlyának (30%) kompenzálásához. A kutatás legnagyobb kihívása az alkalmazási eredmények ipari méretre történő felskálázása. A tudományág sajátossága miatt (bonyolult fizika és nagyszámú paraméter) jól kontrollált és megfelelően leírható eredményeket adó kísérletek nehezen kivitelezhetők, ezért kutatási módszerem alapja a nagy teljesítményű számítástechnika (High Performance Computing, HPC) alkalmazása.

 

A kutatóhely rövid bemutatása

Kutatómunkámat a BME GPK Hidrodinamikai Rendszerek Tanszéken végeztem, Dr. Hegedűs Ferenc témavezetésével. Kutatócsoportunk tevékenysége a szonokémia széles területét lefedi, amely során kihasználjuk a nagy teljesítményű videokártyák által nyújtott számítási kapacitást. A kutatócsoportunk nagy hangsúlyt fektet a nemzetközi kapcsolatok kiépítésére, jelenleg is aktív együttműködés van több neves német kutatóintézettel. Fontosnak tartjuk emellett az utánpótlásnevelést, ezért jelenleg is több BSc és Msc hallgatóval dolgozunk közösen.

A kutatás történetének, tágabb kontextusának bemutatása

A kavitációs buborékok dinamikájának vizsgálata 1917-re nyúlik vissza. A Lord Rayleigh és Milton Plesset után elnevezett Rayleigh-Plesset egyenletet [1] még ma is gyakran alkalmazzák a kavitációs kutatások során. Ekkor a buborékmérethez végtelennek tekinthető folyadéktérbe helyezett ideális gáz és gőz keverékét tartalmazó buborékra úgy tekintenek, mint egy egy szabadságfokú lengőrendszerre, melynek pillanatnyi állapotát az időfüggő buboréksugár írja le. Az ultrahang a folyadéktérben periodikus nyomásváltozást hoz létre, melynek hatására a buborék lengeni kezd. Kellő intenzitású (a nyomásamplitúdó négyzetével arányos) ultrahangos besugárzás felett a buborék a lengése során a méretének többszörösére hízik, majd hirtelen nagy falsebességgel összeroppan. A falsebesség a folyadék hangsebességéhez közeli is lehet, ekkor már szükséges a folyadék összenyomhatóságának figyelembevétele is. Ezért a kutatásaim során a Keller-Miksis egyenletet [3] alkalmaztam, amely első rendig figyelembe veszi a folyadék összenyomhatóságát is.

 

Az ultrahanggal létrehozott akusztikus kavitációs felhőben a buborékok fizikája meglehetősen összetett. Egy buborék az életciklusa során térben vándorol a nyomásgradiens hatására (Bjerknes-erő [4]), diffúziós folyamatokon keresztül hízik, vagy beoldódik a folyadékba [5], interakcióba léphet más buborékokkal, esetleg felbomlik kisebb buborékokra. Az összetett folyamatok és a folyamatokat jellemző eltérő időskálák miatt egy kavitációs felhő vizsgálta meglehetősen összetett, így az alulról fölfelé építkezés elvét követve, egy akusztikus kavitációs felhőt alkotó egyedi buborékok vizsgálatával foglalkoztam. Ez egy jó első megközelítés, mert egy buborék az életciklusa nagy részében a többi buboréktól viszonylag távol esik.

A kutatás célja, a megválaszolandó kérdések

A kutatás célja a szonokémiai alkalmazások hatékonyság-növelésének támogatása numerikus szimulációs eredmények által. A szonokémia, illetve az ehhez szorosan kapcsolódó buborékdinamika jelenleg is aktívan kutatott tudományterület, és számos tanulmány születik évente. E tanulmányok – néhány kivételtől eltekintve – víz közeg alkalmazása mellett készülnek. Nagy viszkozitású közeg esetén nem áll rendelkezésre részletes paramétertanulmány. A nagy viszkozitás nagy csillapítást eredményez, ami csökkenti az összeroppanás erősségét, ezért az alkalmazások egyik korlátja lehet. Másrészt a buborékok felületi dinamikáját leíró differenciálegyenletből látható, hogy a viszkozitás segít a buborék gömb alakjának megőrzésében, ami pedig szükséges az erős, fókuszált és hosszú távú összeroppanó lengések fenntartásához. Az alakinstabil buborékok könnyebben felbomlanak apróbb buborékokra, a kisebb méretű buborékok pedig nehezebben gerjeszthetők a felületi feszültség sugárral fordítottan arányos összehúzó hatása miatt. A dolgozat fő célja olyan optimális viszkózus csillapítás meghatározása, amivel e két kritérium kielégíthető.

 

A vizsgálatok glicerin alkalmazása mellett készültek, amelynek viszkozitása a vízhez képest szobahőmérsékleten három nagyságrenddel nagyobb, továbbá a viszkozitás a hőmérséklet változtatásával két nagyságrendet is változik. Tehát a viszkózus csillapítás mértéke a hőmérséklet változtatásán keresztül befolyásolható. Megjegyzendő, hogy a csillapítás más módon, pl. glicerin-víz keverék használatával, is befolyásolható.

 

Az ultrahangos gerjesztésnek megfelelően a két elsődleges szabad paraméter (a hőmérséklet mellett) a gerjesztés nyomásamplitúdója és frekvenciája. A kutatás során egy átfogó paramétertanulmányt készítettem a nyomásamplitúdó-frekvencia-hőmérséklet paramétertérben az erős összeroppanó, ugyanakkor gömbi alakra stabil buboréklengések feltérképezése érdekében, ezzel támogatva a hatékony üzemeltetési stratégiák kidolgozását.

Módszerek

Az összeroppanó alakinstabil buborék vizsgálatának szokásos módja, hogy a gömbi buborék felületén zavarást írnak elő. A zavarás növekedéséből, illetve csökkenéséből következtetni lehet a buborék alakstabilitására. A megzavart buborék

                                                r(t,Θ,Φ)=R(t)+a_nY_n(Θ,Φ)                                                 (1)

alakú, ahol R(t) az időfüggő átlagos buboréksugár, a_n a felületi zavarás amplitúdója, Y_n(Θ,Φ) pedig az n-edik módushoz tartozó felületi harmonikus függvény. A vizsgálat forgásszimmetrikus alakokra korlátozódik, mivel a buborékot érő külső zavarás általában egy kitüntetett irányból okoz kezdeti deformációt (fal vagy másik buborék közelsége). Ilyen torzult buborék oszcillációkra mutat példát az 1. ábra, ahol az ábra bal oldalán a harmadik, míg jobb oldalt a negyedik módus okozta deformált buborékok láthatóak az idő függvényében.

 

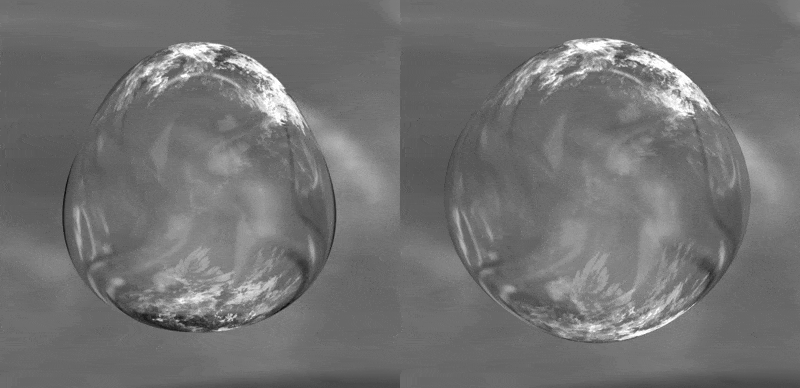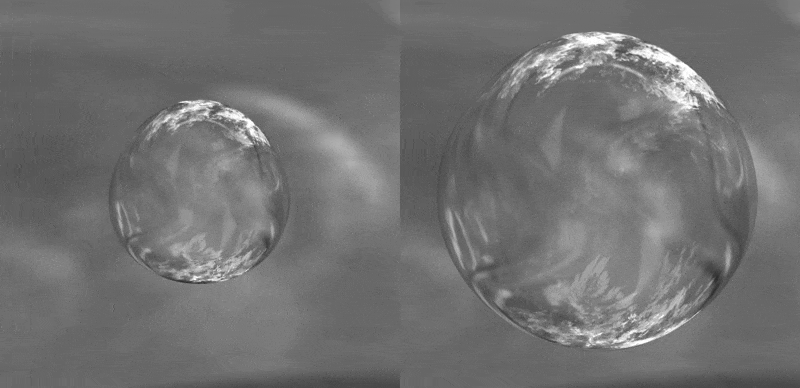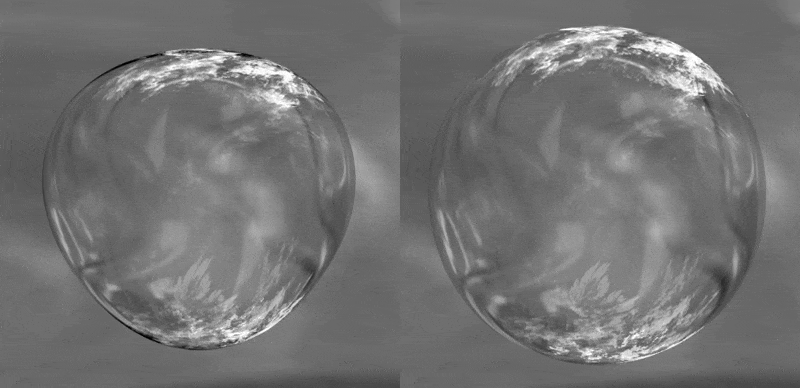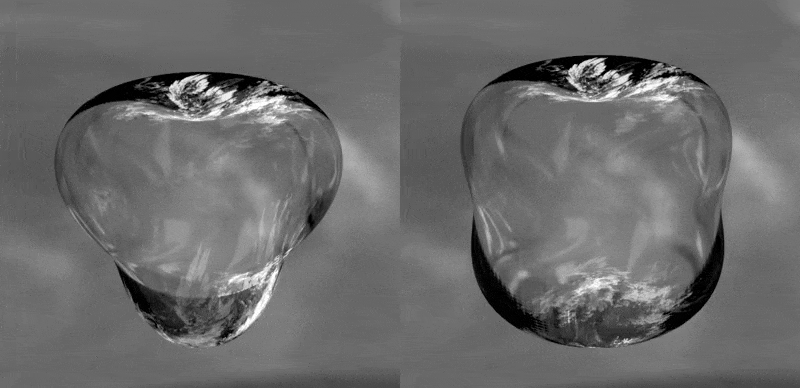
1. ábra: A harmadik és negyedik felületi módus okozta nem gömbi buborék alakok (a jobb láthatóság kedvéért a zavarások mesterségesen fel vannak nagyítva).

 

A számítások során a térfogati lengés modellezésére a Keller-Miksis egyenletet alkalmaztam, amely egy másodrendű nemlineáris közönséges differenciálegyenlet. Megjegyzendő, hogy ez a modell széles paramétertartományon mérésekkel validált, és jól leírja a buboréksugár-idő dinamikát. Az alakstabilitás vizsgálatához a Keller-Miksis egyenlethez csatolni kell egy felületi hullámok dinamikáját leíró közönséges differenciálegyenletet [6], amelyet minden módusra külön-külön kell megoldani.

Eddigi eredmények

Az alakstabil buboréklengések feltérképezésére a környezeti hőmérsékletet 20-70 °C között változtatva 5 °C-ként kétparaméteres paraméter tanulmányokat végeztem a gerjesztési frekvencia-nyomásamplitúdó paramétersíkon. A számítás eredményeként kapott stabilitási térképek láthatóak az 2. ábrán. Az ábrán a frekvencia a buborék sajátfrekvenciájával dimenziótlanítva került feltüntetésre. A stabilitási térképek felbontása p_A×ω_R=500×1151, ezzel egy stabilitási diagram elkészítéséhez kb. 576 ezer szimuláció elvégzését igényli 1 kezdeti feltétel esetén. Ekkora számítási igény mellett elengedhetetlen a haladó programozási technikák és a GPU-k (videokártyák) adta nagy számítási teljesítmény kihasználása. A fehér területek az alakstabil buboréklengést jelölik, míg a színes területek a leginstabilabb, azaz a legrohamosabb növekedést mutató módust ábrázolják a hatodik módusig. Az ábrákon a szonokémiai alkalmazásokhoz szükséges minimális összeroppanás erősség elméleti határát jelentő szintgörbe is feltüntetésre került (vastag fekete görbe).

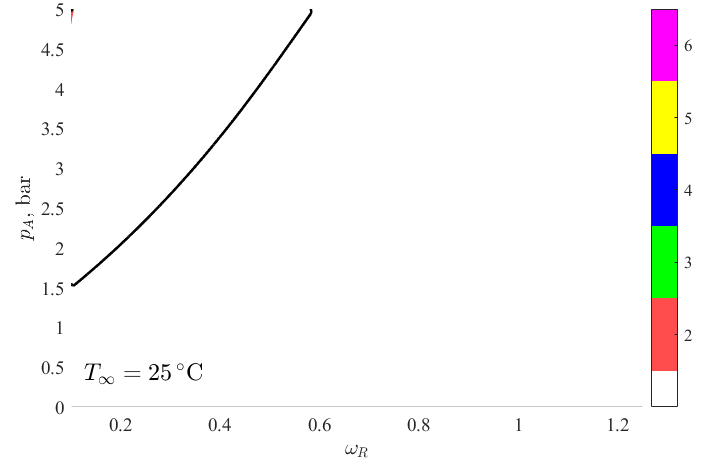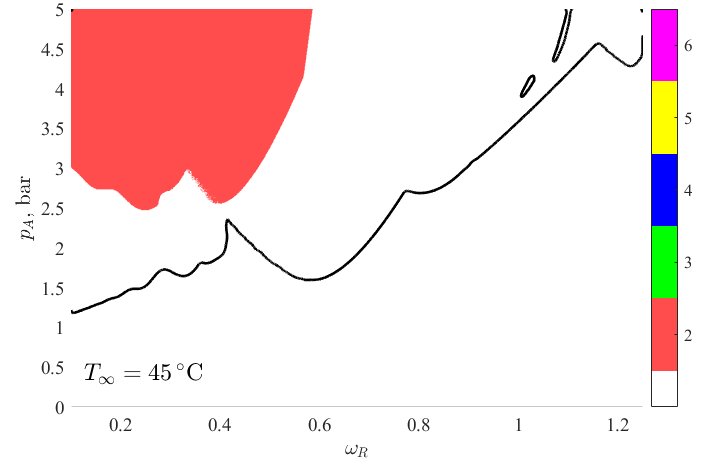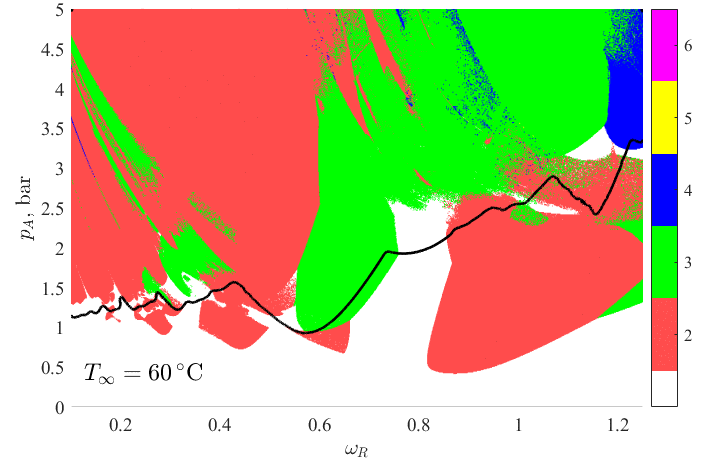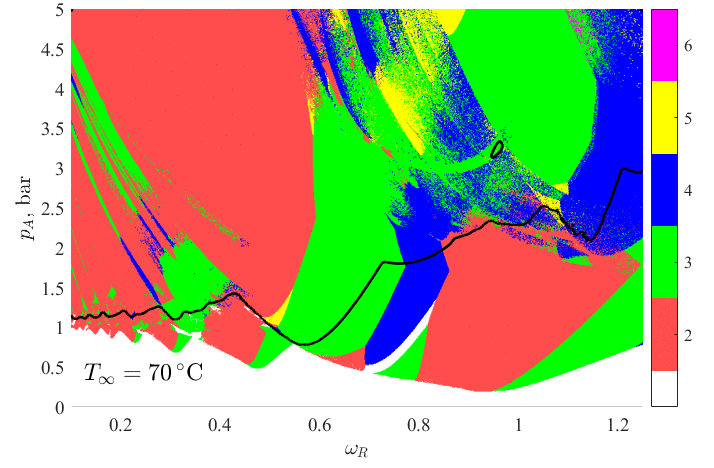
2. ábra: A stabilitási térképek a nyomásamplitúdó és a gerjesztési frekvencia paramétersíkon a környezeti hőmérséklet növelése mellett.

 

Az ábra alapján elmondható, hogy ezek a szintgörbék a kezdeti hőmérséklet növekedésével rohamosan eltolódnak a kisebb amplitúdók irányába, tehát kisebb besugárzási intenzitás is elegendő az aktív kavitáció eléréséhez (kémiai reakciók indukálása). Ez a határ 45 °C környezeti hőmérséklet felett már nem változik jelentősen, azaz adott frekvencián az aktív kavitációs határ eléréséhez szükséges nyomásamplitúdó nem csökkenthető a hőmérséklet további emelésével. Továbbá, magasabb hőmérsékleten, a kisebb viszkozitás a buborék alakstabilitásának elvesztésével jár. Az eredményekből látható, hogy 45–50 °C hőmérséklet-tartományon az alakstabilitás megőrzése mellett már viszonylag alacsony amplitúdó mellett is elérhető a kavitációs határ, azaz e két hőmérsékleti érték között egy optimális viszkózus csillapítás található, ahol kompromisszum érhető el az összeroppanás-erősség és az alakstabilitás között.

 

Várható impakt, további kutatás

A további kutatásaim célja a számítások kiterjesztése kavitációs buborékfelhőkre, ami nagyszámú csatolt Keller-Miksis egyenlet megoldását igényeli. Ezzel lehetővé válna egy szonokémiai reaktor pontosabb modellezése. A megválaszolandó kérdések egyike, hogy az egy buborék szabályozásánál alkalmazott technikákat, mint például a csillapítás az alakstabilitásra, hogyan lehet buborékfelhőkre alkalmazni. Előidézhető-e a buborékok együttes, koherens összeroppanása a viszkozitás szabályozásával növelve a kavitációs aktivitást? Egy ilyen modell kidolgozása a probléma méretéből adódóan nagyságrendekkel nehezebb feladat, így ez még napjainkban is aktívan kutatott terület. Kutatócsoportunk már több mint 2 éve aktívan használja a nagy teljesítményű GPU-programozási technikákat, amely ezen a területen egyelőre egyeduralkodó. Így a buborékfelhők számításánál a csoportunk elsőként érhet el jelentős előrelépést.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

S1. K. Klapcsik, F. Hegedűs, Study of non-spherical bubble oscillations under acoustic irradiation in viscous liquid. Ultrason. Sonochem. 54:256–273, 2018. IF:6,012

S2. K. Klapcsik, R. Varga, F. Hegedűs, Bi-parametric topology of subharmonics of an asymmetric bubble oscillator at high dissipation rate: The exoskeleton, its internal structure and the missing fine substructure, Nonlinear Dyn., 94:2373–2389, 2018. IF: 4,339

S3. K. Klapcsik, F. Hegedűs, The effect of high viscosity on the evolution of the bifurcation set of a periodically excited gas bubble, Chaos Solitons Fract., 104:198–08, 2017. IF: 2,213

S4. F. Hegedűs, K. Klapcsik, The effect of high viscosity on the collapse-like chaotic and regular periodic oscillations of a harmonically excited gas bubble, Ultrason. Sonochem., 27:153–164, 2015. IF: 3,816

S5. K. Klapcsik és F. Hegedűs, Harmonikusan gerjesztett gázbuborék nemlineáris dinamikai vizsgálata nagy viszkozitású folyadékban. in OGÉT 2014. XXII. Nemzetközi Gépészeti Találkozó: 189–185, Nagyszeben, Románia 2014.

S6. K. Klapcsik és F. Hegedűs, Two-Parameter Bifurcation Analysis for the Seeking of High Amplitude Oscillation of a Periodically Driven Gas Bubble in Glycerine. in Proceedings of Conference on Modelling Fluid Flow (CMFF’15): 16th event of the International Conference Series on Fluid Flow Technologies, paper 116. p 8, Budapest, 2015.

S7. F. Hegedűs, R. Varga és K. Klapcsik, Bifurcation Structure Of A Periodically Driven Bubble Oscillator Near Blake’s Critical Threshold. in Proceedings of Conference on Modelling Fluid Flow (CMFF’15): 16th event of the International Conference Series on Fluid Flow Technologies, paper 115. p 8., Budapest, 2015.

S8. R. Varga, K. Klapcsik és F. Hegedűs, Towards Physical Modeling of the Utilization of Ultrasound in Modern Medical Therapeutic Applications. in First European Biomedical Engineering Conference for Young Investigators (ENCY 2015):114–117, Budapest, 2015.

S9. K. Klapcsik és F. Hegedűs, Modelling of non-spherical bubble shape oscillations in viscous liquid. in Proceedings of the 5th International Scientific Conference on Advances in Mechanical Engineering (ISCAME 2017):261–267, Debrecen, 2017.

 

Linkgyűjtemény

http://www.hds.bme.hu/research/BubbleDynamics/index.html

https://www.gpuode.com/

 

Hivatkozások listája.

[1] C. E. Brennen, Cavitation and Bubble Dynamics. Oxford University Press, New York, 1995.

[2] K. Yasui, Acoustic Cavitation and Bubble Dynamics. Springer International Publishing, Cham, 2018.

[3] J. B. Keller, M. Miksis, Bubble oscillations of large amplitude. J. Acoust. Soc. Am., 68(2):628–633, 1980.

[4] I. Akhatov, R. Mettin, C. D. Ohl, U. Parlitz, és W. Lauterborn, Bjerknes force threshold for stable single bubble sonoluminescence. Phys. Rev. E, 55:3747–3750, 1997.

[5] M. M. Fyrillas, A. J. Szeri, Dissolution or growth of soluble spherical oscillating bubbles. J. Fluid Mech., 277:381–407, 1994.

[6] J. Holzfuss. Surface-wave instabilities, period doubling, and an approximate universal boundary of bubble stability at the upper threshold of sonoluminescence. Phys. Rev. E, 77(6):066309, 2008.