Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék

Témavezető: Dr. Csernák Gábor

A mikro-káosz elméleti és kísérleti vizsgálata

A kutatási téma néhány soros bemutatása

A kutatási téma fő fókusza a mikrokáosz (kis amplitúdójú kaotikus rezgés) jelenségének mély megértése. A mikrokaotikus viselkedés tipikusan számítógéppel szabályozott rendszerekben jelenik meg digitális hatások (mintavételezés, kerekítés, időkésés) együttes jelenlétéből fakadóan.

 

A kutatóhely rövid bemutatása

A kutatás helye a Műszaki Mechanikai Tanszék. A tanszéken nemzetközileg elismert, kimagasló színvonalú kutatási munka folyik számos alkalmazott mechanikai tudományterületen. Ezt illusztrálják a SIREN ERC projekt, az emberi egyensúlyozással foglalkozó Lendület kutatócsoport, valamint az MTA-BME Gépek és Járművek dinamikája kutatócsoport eredményei.

 

A kutatás történetének, tágabb kontextusának bemutatása

Napjainkban széles körben elterjedtek a számítógéppel szabályozott berendezések (gyártósorokon működő robotok, 3D-nyomtatók vagy éppen az épületautomatizálás berendezései), melyek tervezése és ellenőrzése új kihívásokat jelent. A digitális szabályozás általában ütemesen, ún. mintavételezési időpillanatokban történik. Ekkor az aktuális állapot megvizsgálása után a számítógép kiszámítja a szükséges beavatkozás mértékét, majd vezérli az egyes beavatkozó komponenseket. Tipikusan jelen van időkésés is, ugyanis az aktuális állapot mérése és a beavatkozás között valamennyi számítási időre van szükség. Mivel a digitális jelek véges sok biten vannak ábrázolva, az analóg-digitális átalakítások során kerekítés is történik.

E három digitális hatás (mintavételezés, időkésés és kerekítés) bizonyos körülmények között kismértékű, de kaotikus rezgésekhez, mikrokáoszhoz vezet.

 

A mikrokáosz jelenségének felismerése Dr. Stépán Gábor, Dr. Haller György és Dr. Eniko Enikov nevéhez fűződik [1, 2], és a 90-es évek második felére tehető. Az elmúlt két évtizedben pedig Dr. Csernák Gábor vizsgálta aktívan a vonatkozó tudományterületeket.

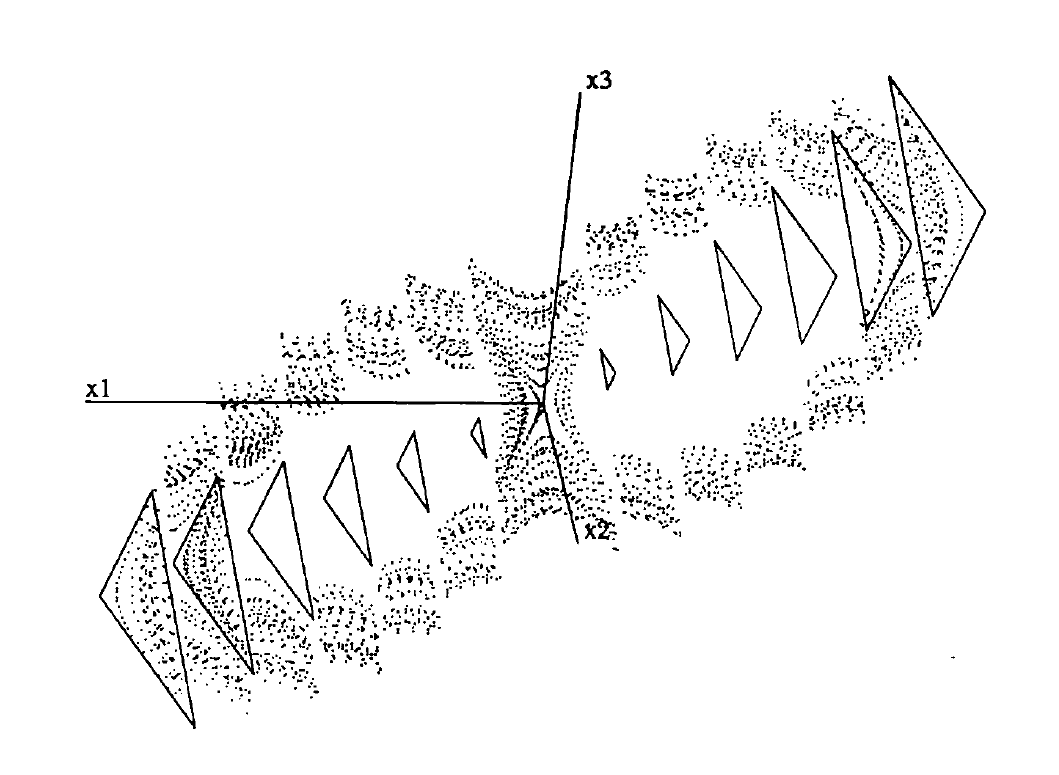
1. ábra: Különös attraktor egy mikrokáosz leképezés fázisterében [1].

 

A mikrokáoszt kis amplitúdója miatt a gyakorlatban sokszor elhanyagolják, vagy véletlenszerű zajnak tekintik, azonban ez a lépés megakadályozza a mikrokaotikus viselkedés mögöttes mintázatainak megfigyelését, vagy éppen azt, hogy adott helyzetben előnyt kovácsoljunk a viselkedés jelenlétéből.

A kutatás célja, a megválaszolandó kérdések.

Az egyik legegyszerűbb rendszer, amin megmutatható a mikrokaotikus viselkedés, a mintavételezéses szabályozású inverz inga (lásd 2. ábra).

 

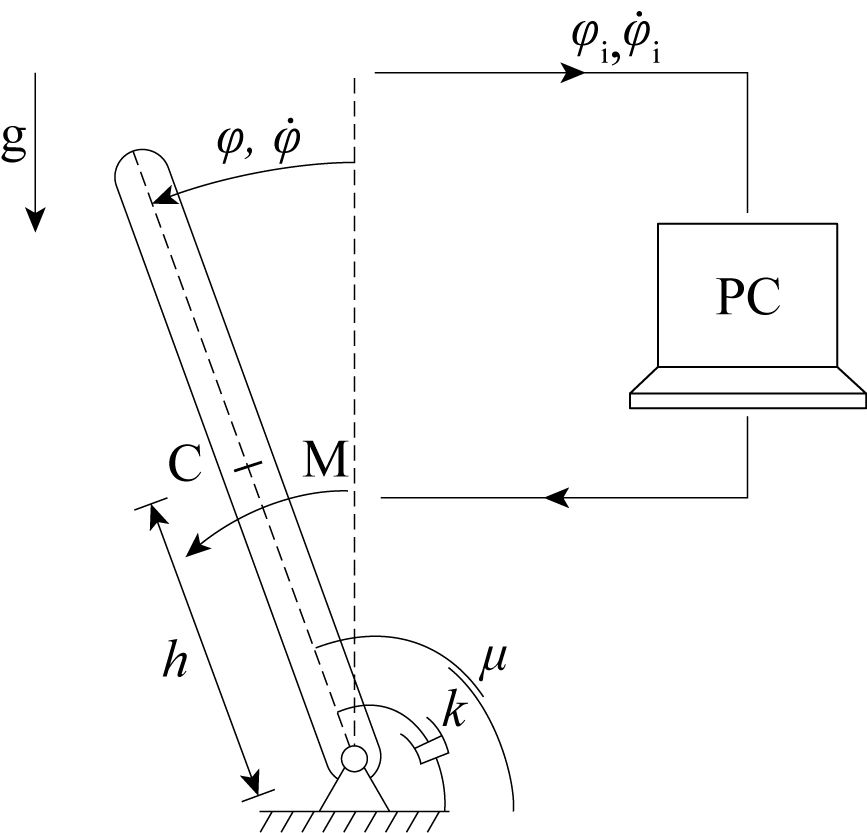
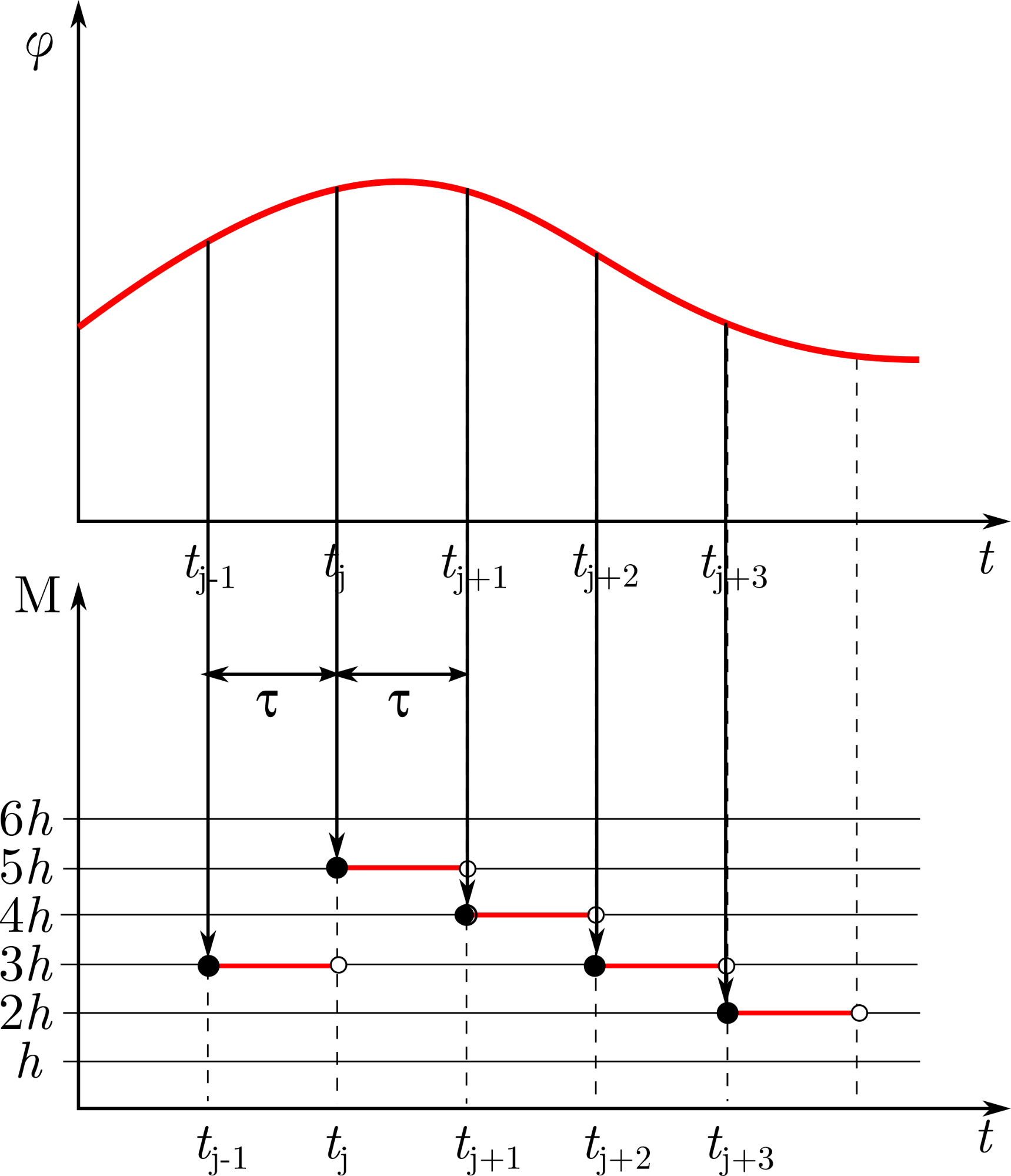
2. ábra: A digitálisan szabályozott inverz inga [G1].

 

Ebben a modellben a számítógép periodikusan méri az inga kitérését és szögsebességét (mintavételezés), és a szabályozási stratégia alapján kiszámított szabályozó nyomatékot kerekítve vezérli ki. A szabályozó célja az inga fenti egyensúlyi helyzetének stabilizálása.

Az inga mozgását ábrázolhatjuk a pozíció-sebesség fázisterében, és ezáltal megérthetjük, hogy miért alakul ki szabálytalan rezgés.

A kívánt felső instabil egyensúlyi helyzet körül a szabályozásnak a kerekítés miatt holtsávja van, azaz nem vezérel ki nyomatékot. A holtsáv mellett párhuzamos sávok tartoznak az egyes kivezérelt nyomaték értékekhez, a sávokat pedig (feketével jelölt) kapcsolóvonalak választják el egymástól. Ha az inga elkezd dőlni, a szabályozó addig nem avatkozik be, amíg az inga be nem lép a minimálisan kivezérelhető nyomatékhoz tartozó sávba. Ezután a szabályozó várhatóan visszalöki az ingát a holtsávba és így két sáv között fog ide-oda mozogni az inga a fázistérben.

A szabályozás nem azonnal észleli azt, hogy az inga belép egy szabályozási sávba, mert csak a mintavételezési pillanatokban ellenőrzi az inga állapotát, emiatt véletlenszerű ideig haladhat az inga az aktuális nyomatékhoz tartozó sávon kívül, mielőtt a szabályozó észleli a változást és aktualizálja a szabályozó nyomaték értékét.

Jól illusztrálja mindezt az 1. videó, melyben kaotikus rezgés látható a holtsáv és az első jobb oldali sáv határán, később azonban (1:00-tól) az is látható, hogy a rendszer képes átbillenni a baloldalra, és valójában a jobb- és baloldalon található repellorok alkotnak egy szimmetrikus attraktort a fázistérben.

1. videó: A mikrokaotikusan viselkedő inverz inga fázistere

 

Amennyiben a videóban illusztrált mozgás mintavételezési időpillanatokhoz tartozó állapotait egy-egy ponttal ábrázoljuk, kirajzolódik a fraktálszerű, szimmetrikus attraktor képe:

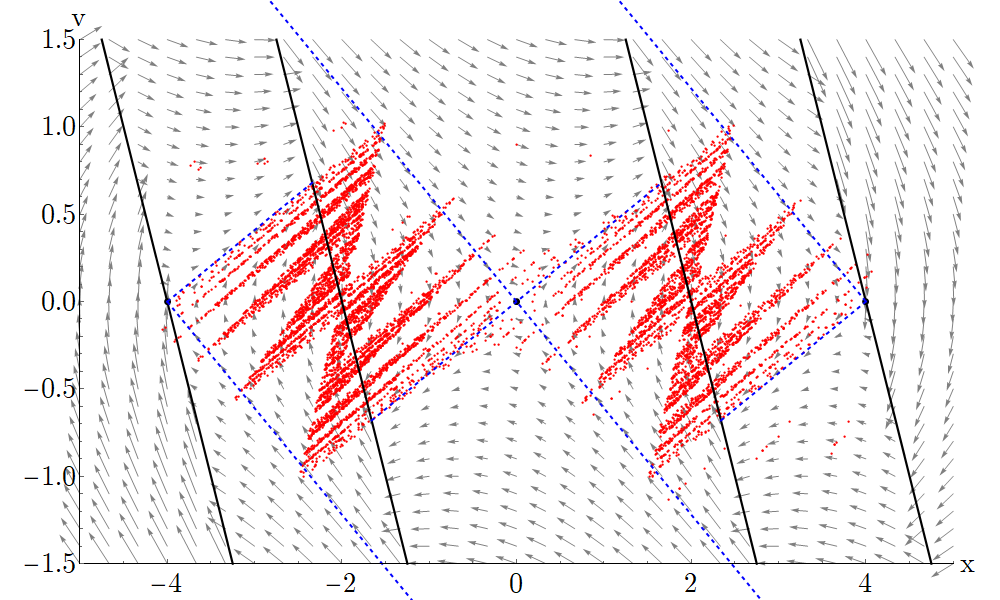
3. ábra: Az 1. videóban illusztrált mozgás által lefedett kaotikus attraktor.

 

Látható tehát, hogy már két digitális hatás (mintavételezés és kerekítés) is képes különös, kaotikus oszcillációkat produkálni, és ezáltal jelentős szabályozási hibát okozni.

Kutatásom során az alábbi kérdésekre keresem a válaszokat:

●     Hogyan lehet feltérképezni a fázistér felépítését? Hány attraktor vagy repellor található benne, és milyen tulajdonságokkal rendelkeznek?

●     Milyen szabályozási stratégiákkal lehet átrendezni a fázisteret úgy, hogy a szabályozási hiba minél kisebb legyen?

 

Módszerek

Analitikus vizsgálatok és szimulációk:

A mikrokáosz ún. mikrokáosz-leképezéssel írható le [G2]. A leképezés bizonyos tulajdonságait analitikus úton meg lehet állapítani, hasonlóképpen a fázistérben található kapcsolóvonalak, egyensúlyi helyzetek, valamint és ezek kölcsönhatásai is vizsgálhatóak.

Szimulációk segítségével belátható, hogy nemcsak a rendszerparaméterek variálása, hanem a kezdeti feltételek megváltoztatása is befolyásolja a mikrokaotikus viselkedést. Bizonyos kezdeti feltételek esetén a rendszer a kívánt egyensúlyi helyzethez közelebb eső attraktorba jut (lásd 4. ábra), így a szabályozási hibát döntően befolyásolhatja a kezdeti feltételek megválasztása is.

 

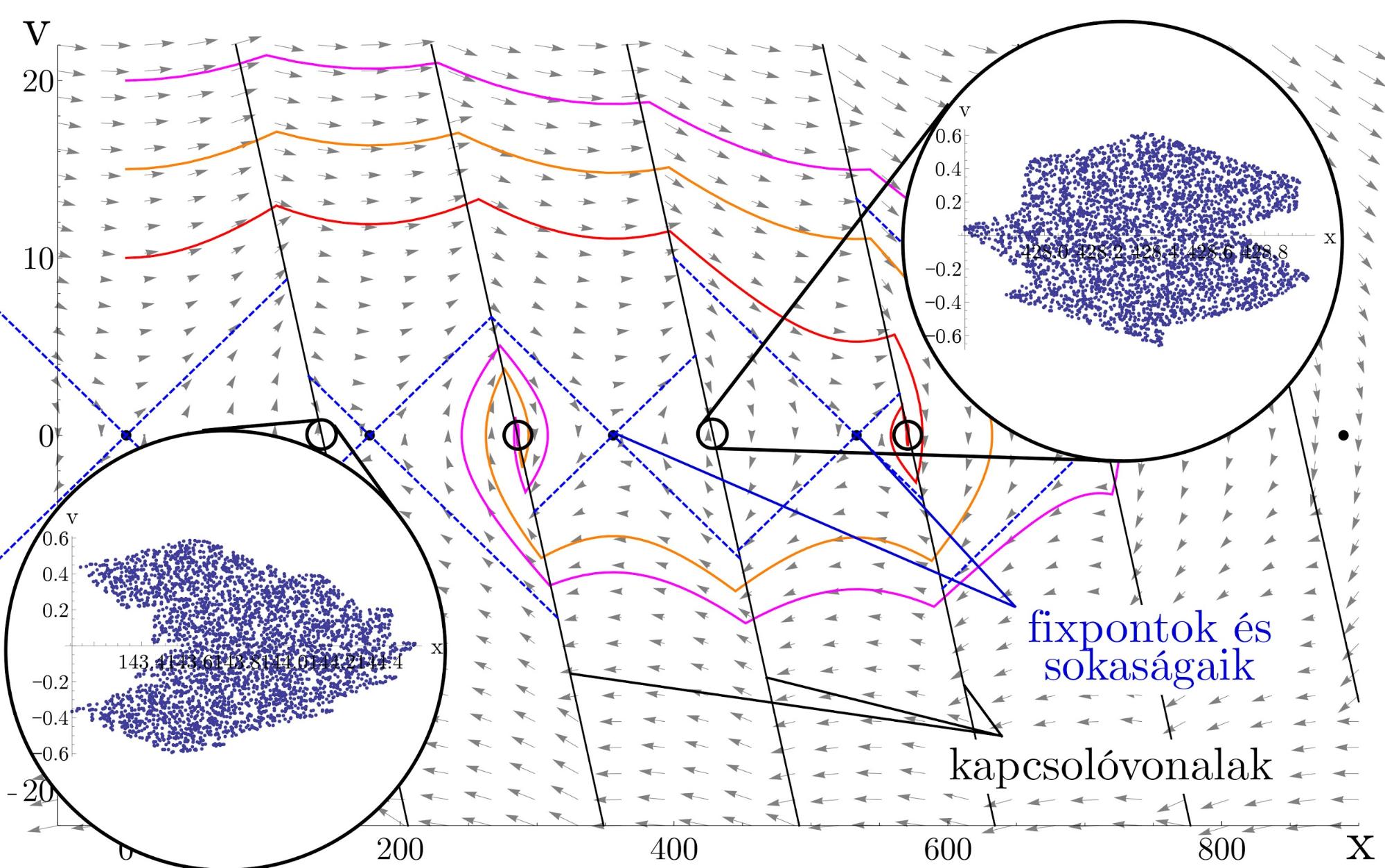
4. ábra: A kezdeti feltételek hatása; a kezdősebességtől függően az inga más attraktorba jut.

 

A fázistér feltérképezése nem egyszerű feladat; numerikus szimulációk különböző kezdeti feltétellel induló megismétlésével rendkívül idő- és számításigényes eljárás lenne, ráadásul hosszú tranziens kaotikus viselkedés esetén a szimulációk korai megállítása hibákhoz vezet. Emiatt kutatómunkám során a 90-es években kifejlesztett cellaleképezést használtam, mely kiváló eszköznek bizonyult a fázistér vizsgálatára.

 

Cellaleképezés

A cellaleképezés során a fázisteret diszkretizáljuk – cellákra bontjuk –, ezután pedig minden cellához egy vagy több képcellát rendelünk, ahova a dinamika az adott cellából vezet. Az egyszerű cellaleképezés (SCM: simple cell mapping) esetén minden cellához egyetlen kép tartozik, és a képek láncolatának végigkövetésével periodikus pályákat vagy periodikus pályákra vezető tranziens cella-láncokat találhatunk a fázistérben (lásd 5. ábra). Kaotikus rendszerek esetén a nagy periodicitású pályák tipikusan kaotikus attraktorokat fednek le, a hozzájuk tartozó tranziens cellák pedig a vonzási tartományt alkotják.

 

5. ábra: Az egyszerű cellaleképezés illusztrációja. Minden cellához egyetlen képcella tartozik, a képek láncolatának követésével periodikus pályák (pl. ABCD cellák) fedezhetők fel.

 

A cellaleképezés számítási ideje a feltérképezni kívánt fázistér-tartomány méretével arányos, emiatt nagyságrendekkel gyorsabb, mint ismételt szimulációk futtatása.

Kihívást jelenthet azonban a feltérképezendő fázistérrégió kiválasztása, emiatt továbbfejlesztettem az egyszerű cellaleképezést, és létrehoztam az adaptív, csoportosított cellaleképezést [G3], mely képes a vizsgált fázistér-tartomány automatikus kibővítésére, valamint párhuzamos futtatást is lehetővé tesz. A csoportosított cellaleképezést illusztrálja a 6. ábra, melyen két cellaleképezéses megoldás összeillesztése, és ezáltal egy új periodikus pálya (középen narancssárga cellák) felfedezése látható.

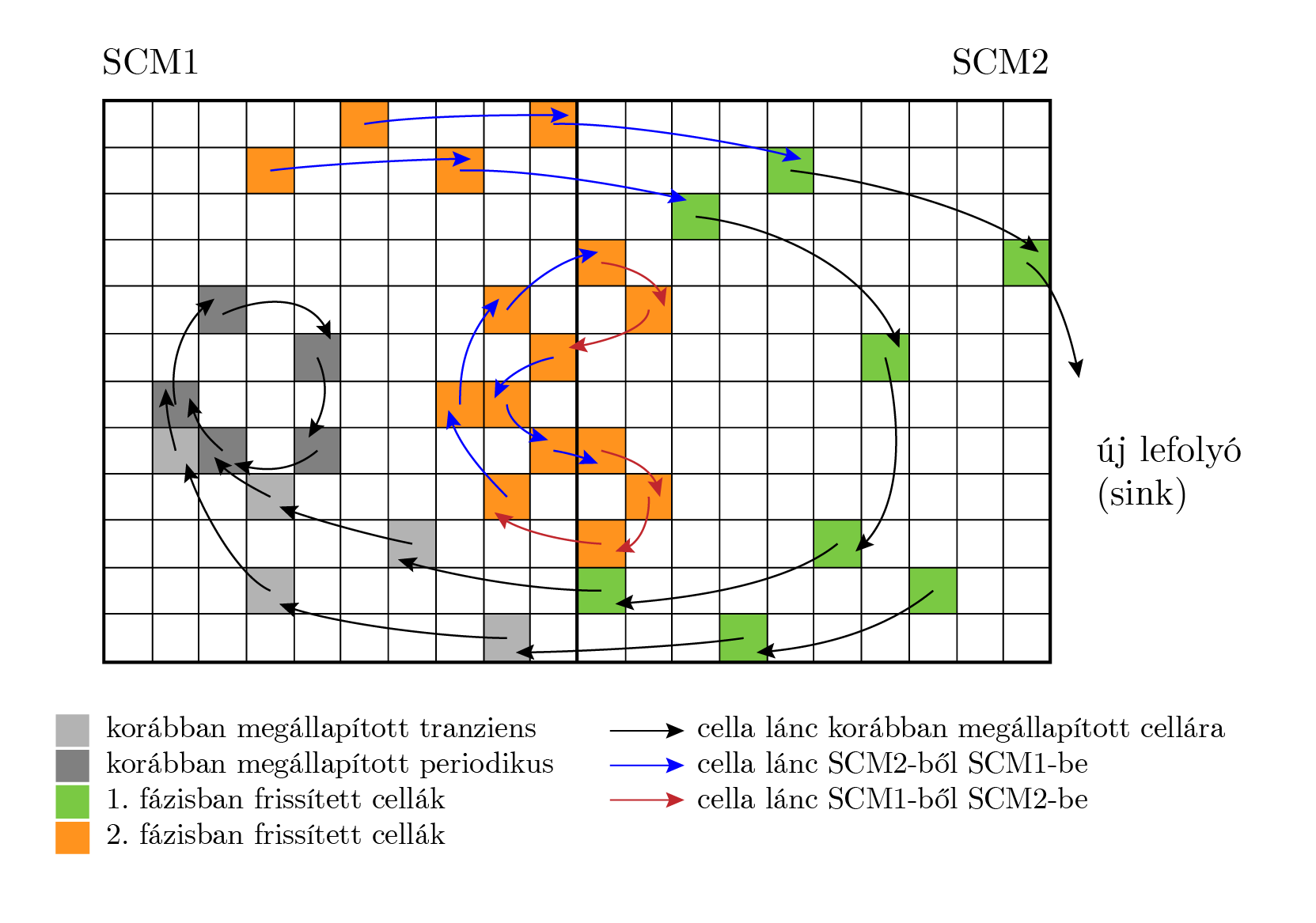
6. ábra: Az adaptív, csoportosított cellaleképezés illusztrációja: a fázistér-tartomány bővítése után a két régióban érvényes cellaleképezéses eredményeket összeilleszti az algoritmus, ezáltal új periodikus pályát fedez fel. [G3]

 

Eddigi eredmények

A cellaleképezéses módszerek segítségével nyert eredményekkel számos, az analitikus vizsgálatok során alkotott elméletet igazoltam. A fenti inverz inga esetében a fázistérben nyeregpontok és attraktorok sormintája követi egymást, és a rendszer vagy szabályozás paramétereinek variálásával ezt a mintázatot befolyásolhatjuk. Így adott esetben a kívánt helyzettől távol elhelyezkedő kaotikus attraktorok a megfelelő paraméter megváltoztatásával megszüntethetőek (lásd 7. ábra).

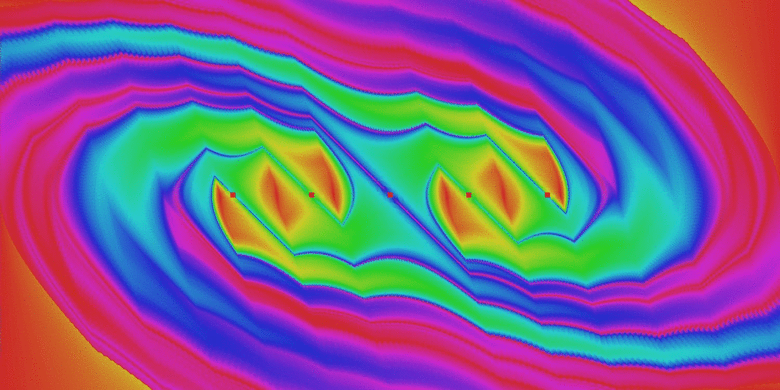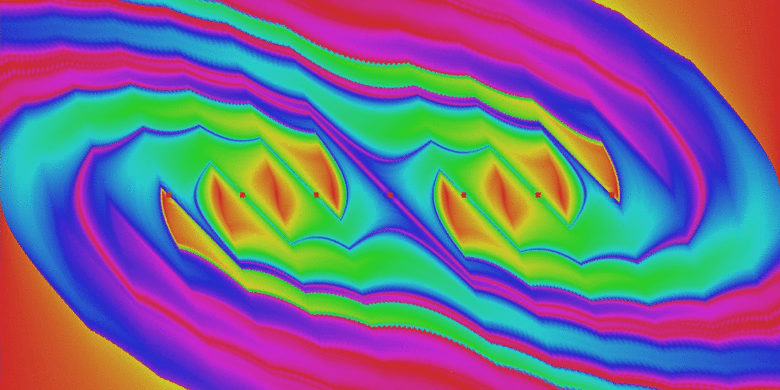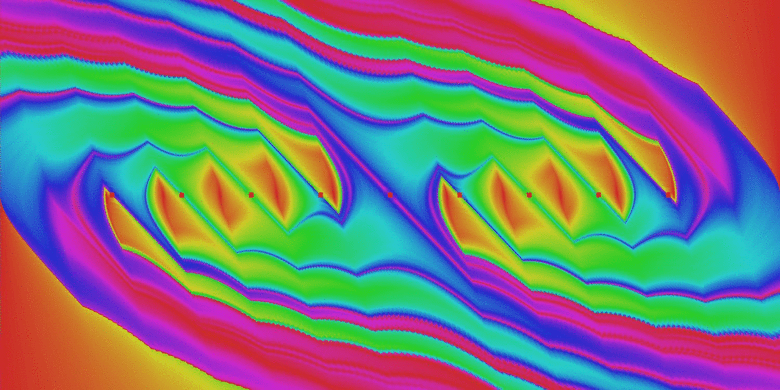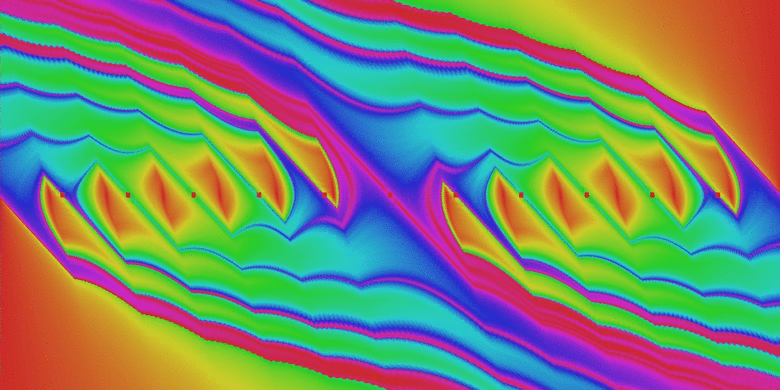
7. ábra: Az inverz inga fázisterének szerkezete a rendszerparaméter kismértékű változtatása esetén. Kezdetben mindkét oldalon három, végül pedig 6-6 db attraktor található (az attraktorok narancssárga környezetű piros foltokkal vannak jelölve).

 

A cellaleképezéses eredmények segítségével a rendszer és szabályozási paraméterek széles skáláját megvizsgáltam, így az egyes rendszerjellemzők változtatásának lehetséges hatásait megmutattam. [G7] A futtatások során nagy segítséget jelentett a BME szuperszámítógépe is.

 

2019-ben elkészültem az általam megvalósított cellaleképezéses algoritmusok nyílt forráskódú csomagjával (cell-mapping C++ library) mely lehetővé teszi a többprocesszoros számítási környezetek hatékony használatát. Minden korábbinál nagyobb cellaleképezéses szimulációkat készítettem (4 milliárd cella), melyek segítségével egyszerre látható a fázistér globális szerkezete, valamint az attraktorok és vonzási tartományok fraktálszerkezete.

 

8. ábra: (Kattintson a képre) 4 gigapixeles cellaleképezéses szimuláció a mikrokáosz leképezés fázisteréről. A színes tartományok különböző kaotikus attraktorok vonzási tartományai, az x-tengelyen a tartományok belsejében kaotikus, fraktálszerű attraktorok találhatóak.

 

Kimutattam, hogy a mikrokaotikus viselkedés száraz súrlódás jelenlétében is megmarad [G5, G8]. A felső instabil helyzetet stabilizálhatja a súrlódás, de kis kezdősebességek esetén távoli kaotikus attraktorokba jut az inga. (Lásd 9. ábra.)

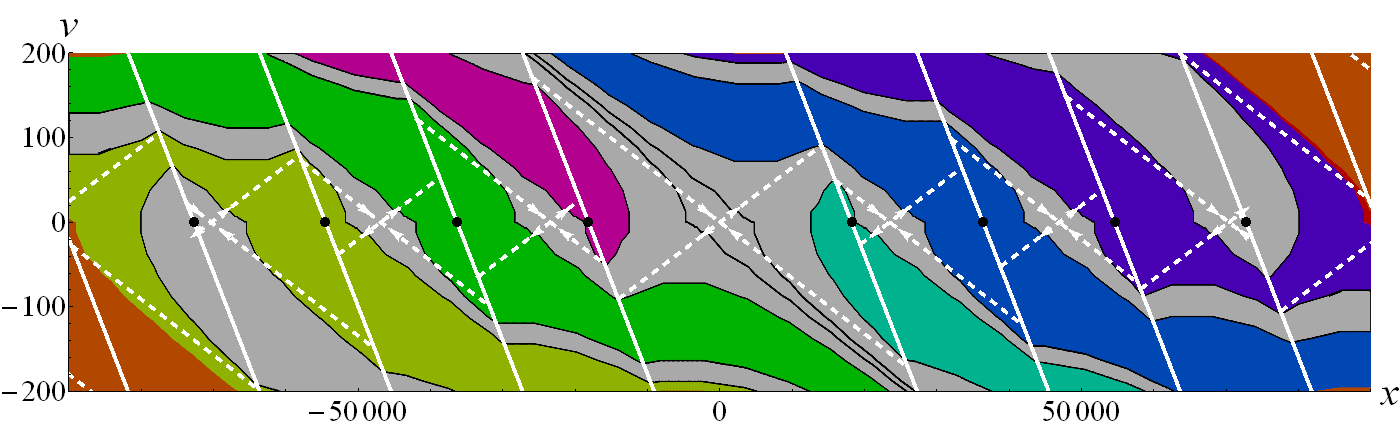
9. ábra: A száraz súrlódásos inverz inga fázistere. A szürke zónák a súrlódásos letapadáshoz tartozó régiókat jelölik. A színes régiók kaotikus attraktorok vonzási tartományai. [G5]

 

Bebizonyítottam, hogy bizonyos kerekítési esetek esetén a különálló kaotikus attraktorok helyett olyan periodikus pályák jelennek meg a fázistérben melyekre kaotikus oszcilláció szuperponálódik [G6]. Adott esetben akár több, egymást körülvevő ilyen periodikus pálya is jelen lehet, és a megoldás ezek között átjárhat (azaz több valójában instabil pálya alkot közösen egy stabil periodikus pályát, melyre kaotikus rezgés rakódik), lásd 10. ábra.

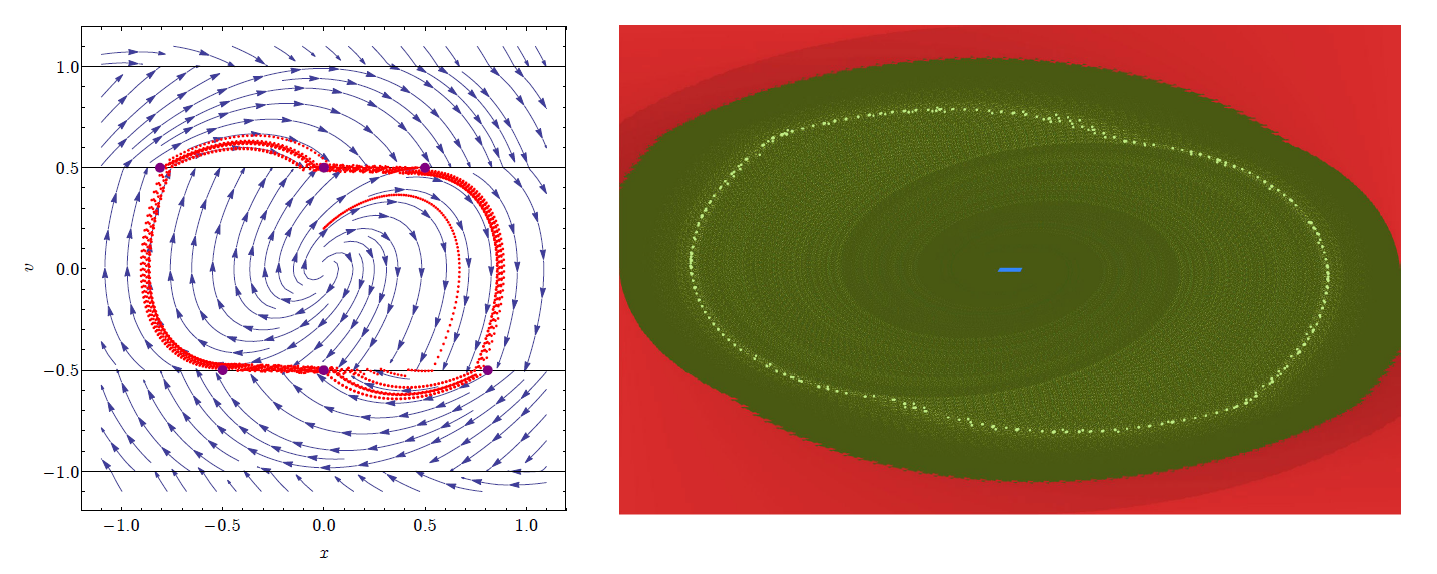
10. ábra: Periodikus pályára szuperponálódó kaotikus rezgés D szabályozás esetén. A baloldalon az analitikus, a jobboldalon pedig a cella-leképezéses eredmény látható.

 

Vizsgáltam a valóságot leginkább leíró ún. kettős kerekítéses esetet, amelyben a mért jelek és a beavatkozó erő / nyomaték is kvantálva van [G9]. Kísérleteket végeztem direkt hajtású inverz ingákkal melyeket mikrokontrollerek vezérelnek (lásd 11. ábra) [G5]. A kísérleti berendezés legújabb generációjával sikerült olyan méréseket végeznem, melyekből kísérletileg is bizonyítható a káosz. Egy ilyen mérést szemléltet a 12. ábra és a 2. videó.

 

11. ábra: A kísérleti berendezés két generációja. 1: inverz inga, 2: motor és enkóder, 3: motorvezérlő (H-híd), 4: mikrokontroller.

 

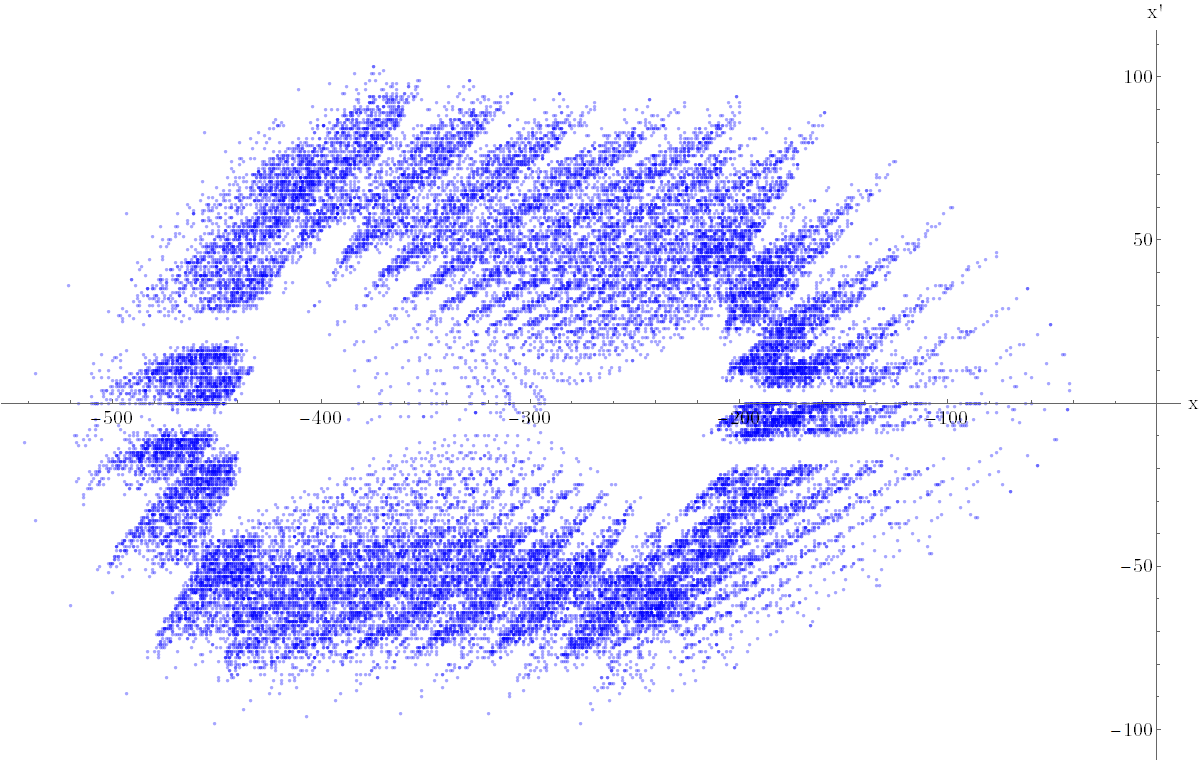
12. ábra: Méréssel rögzített kép kaotikus attraktorról. Az attraktor közepén instabil nyeregpont található, jól látható a fűrészfog-szerű fraktálszerkezet mely a mikrokáoszra jellemző.

 

2. videó: Mikrokaotikus oszcilláció kettős-kerekítés esetén (mesterségesen felnagyított kerekítéssel). A videóban látható oszcilláció során mért pozíció-sebesség diagram a 12. ábrán látható.

 

Várható impakt, további kutatás

Az eddigi kutatómunka egyik fontos eredménye a cellaleképezéses módszercsalád népszerűsítése, és a mikrokáosz vizsgálatára alkalmas cellaleképezéses módszerek kifejlesztése. A többprocesszoros számítógépek és a párhuzamos számítás elterjedésével az adaptív csoportosított cellaleképezés várhatóan hasznos eszköz lesz a hasonló problémákat vizsgáló kutatási területeken is.

 

Kiemelt fontosságú továbbá a mikrokáosz jelenségének széles körű bemutatása. A gyakorlatban sokszor elhanyagolják, vagy zajjal helyettesítik a kaotikus oszcillációkat, de az eddigi eredmények bizonyítják, hogy ez legtöbbször nem célravezető.

A mikrokáosz kettős-kerekítés formalizmusával valamint a súrlódás hatásának figyelembe vételével sikerült kísérleti körülmények között is kimutatni a mikrokáoszt, az eredményekre épülő publikációk várhatóan segítik majd a mikrokáosz tématerületének népszerűsítését.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája:

[G1.]             Gyebrószki Gergely, Dr. Csernák Gábor: Digitális szabályozás okozta kaotikus rezgés amplitúdójának becslése, XII. Magyar Mechanikai Konferencia, (2015.08.25-27.), Miskolc, Magyarország

[G2.]             Dr. Csernák Gábor, Gyebrószki Gergely, Dr. Stépán Gábor: Multi-Baker Map as a Model of Digital PD Control, International Journal of Bifurcation and Chaos (IJBC), 26(2), 2016, pp. 1650023 1–11

[G3.]             Gyebrószki Gergely, Dr. Csernák Gábor: Clustered Simple Cell Mapping: An extension to the Simple Cell Mapping method, Communications in Nonlinear Science and Numerical Simulation 42, 2017, pp. 607–622

[G4.]             Gyebrószki Gergely, Csernák Gábor: Methods for the quick analysis of micro-chaos, Applied Nonlinear Dynamical Systems in Proceedings in Mathematics and Statistics in Springer Series (ISBN: 978-3-319-08265-3), 93 2014, pp. 383–395

[G5.]             Gyebrószki Gergely, Csernák Gábor, Budai Csaba: Experimental investigation of micro-chaos, 8th European Nonlinear Dynamics Conference (2014.07.06–11), Bécs, Ausztria

[G6.]             Gyebrószki Gergely, Nagy Péter Tamás, Csernák Gábor: Numerical Exploration of Micro-chaotic Behaviour, Finno-Ugric International Conference on Mechanics – 2013, book of abstracts

[G7.]             Gyebrószki Gergely, Dr. Csernák Gábor: Inherent control error in a multi-PD controlled double inverted pendulum, Proceedings of the 9th European Nonlinear Dynamics Conference. 2017. pp. 238-1–238-5

[G8.]             Gyebrószki Gergely, Dr. Csernák Gábor: The Hybrid Micro-chaos Map: Digitally Controlled Inverted Pendulum with Dry Friction, Periodica Polytechnica Mechanical Engineering, 63(2), pp. 148–155.

[G9.]             Gyebrószki Gergely, Dr. Csernák Gábor: Twofold quantization in digital control: deadzone crisis and switching line collision, Nonlinear Dynamics, 2019. (benyújtva, bírálat alatt)

 

Linkgyűjtemény:

1. Amikor a robot keze megremeg: digitálisan szabályozott gépek kaotikus rezgései
2. Szabadon elérhető könyv a káoszról

 

Hivatkozások listája:

[1]   Enikov, E., and Stépán, G., Micro-chaotic behavior of digitally controlled machines, in Proc. 15th ASME Biennial Conference on Mechanical Vibration and Noise (Boston, 1995).

[2]   G. Haller, G. Stépán: Micro-chaos in digital control, Journal of Nonlinear Science, 1996, Volume 6, Number 5, Page 415

[3]   C.S. Hsu: Cell-to-Cell Mapping: A Method of Global Analysis for Nonlinear Systems, Applied Mathematical Sciences 64, 1987, Springer, Singapore