Fizikai Tudományok Doktori Iskola 

BME TTK, Atomfizika Tanszék

Témavezető: Dr. Gali Ádám

Gyémántalapú kvantumbitek vizsgálata első elvű módszerekkel

A kutatási téma néhány soros bemutatása

A kvantumtechnológia és kvantuminformáció tudománya kiemelt kutatás-fejlesztési terület az EU-ban és az egész világon, amely új számítási és kommunikációs eszközök, illetve szenzorok kifejlesztéséhez vezethet. A kvantumbitek egyik lehetséges fizikai implementációja a paramágneses és optikailag is aktív ponthibák szilárdtestekben [1], melyek közül a gyémántbeli hibacentrumokat vizsgáltam meg atomi szintű számítógépes szimulációs eszközökkel.

A kutatóhely rövid bemutatása

Munkámat Dr. Gali Ádám kutatócsoportjában végzem az Atomfizika Tanszéken és a Wigner Fizikai Kutatóközpontban. A nagy számításigényű, atomi szintű szimulációkat a kutatócsoport saját számítógépklaszterén, továbbá a NIIFI által üzemeltetett magyarországi szuperszámítógépeken végezzük, ahol akár több terrabájt memória, illetve több száz processzormag használatára is van lehetőség.

A kutatás történetének, tágabb kontextusának bemutatása

A gyémántbeli kvantumbitek egyik legismertebb úttörő képviselője a nitrogénvakancia- (NV) centrum [2]. Erre a centrumra az jellemző, hogy magas spinű alapállapottal rendelkezik, amelyet optikai gerjesztéssel közel 100%-ban spinpolarizálni lehet, akár szobahőmérsékleten is. A fotogerjesztésből származó lumineszcenciajel intenzitása függ az alapállapot spinállapotától. Így optikailag alaphelyzetbe állítható és egyben kiolvasható az elektronspin állapota, amelyet mikrohullámú térrel lehet manipulálni. Konfokális mikroszkóp segítségével egyetlenegy NV-centrum spinje manipulálható, megvalósítva a kvantumbitet. Az NV-centrum tulajdonságai azonban nem minden szempontból ideálisak pl. kvantumkommunikációra. Emiatt fontos a gyémántban olyan alternatív ponthibák keresése, amelyek szándékosan vagy spontán jutnak be, és alkalmasak lehetnek kvantumtechnológiai alkalmazásokra. Emellett általánosan fontos az optikailag aktív vagy paramágneses ponthibák azonosítása, amelyek befolyásolhatják a gyémántbeli kvantumbitek működését. 

Azokat a ponthibákat vizsgáltam meg, amelyek spontán kialakulhatnak a gyémánt kémiai gőzleválasztása (CVD - chemical vapor deposition) során. Ezek az oxigén és hidrogén-, valamint a heteroepitaxiális növesztés esetén, a szilíciumszennyezők, amely pl. a szilíciumvakancia- (SiV) hibát [3], egyben kvantumbitet hozza létre. Emellett szándékosan, implantációval germániumvakancia- (GeV) [4] és ónvakancia- (SnV) [5] centrumokat (1. ábra) is létrehoztak új kvantumbitek megvalósítása céljából.

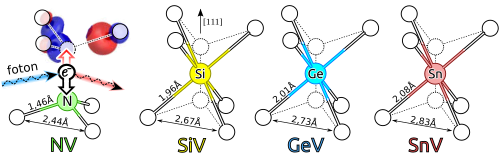
1. ábra: A nitrogénvakancia (NV), és a szilícium-, germánium-, ónvakancia- (SiV, GeV, SnV) centrumok geometriai struktúrája. Az NV-centrum elektronspinje megvilágítás hatására alaphelyzetbe hozható

A kutatás célja, a megválaszolandó kérdések

Bár a fent bemutatott NV-centrumot már több mint egy évtizede használják kvantumbitként, ennek ellenére még nem ismert pontosan, hogy miként zajlik ez a folyamat. Korábbi tanulmányok alapján az NV-centrumban a spinfüggő fluoreszcenciáért az alap- és gerjesztett triplett állapotok közötti szingulett állapotok közötti rendszerszintű átmenetek a felelősek, de a kísérleti megfigyeléseket nem sikerült a korábbi elmélettel pontosan leírni. Egyik célkitűzésünk az volt, hogy a rendszerközi átmenetek mikroszkopikus elméletét kidolgozzuk az NV-centrumra.

Az NV-centrum mellett más ponthibákat is megvizsgáltam, amelyek spontán vagy szándékoltan kerülnek a gyémántba. Az oxigén spontán juthat be a gyémántba, de szinte semmit sem tudunk a gyémántban lévő oxigénről. Azt tűztem ki célul, hogy számításokkal felderítsem a legfontosabb oxigénhibákat, és a legfontosabb magneto–optikai paraméterek számolásával jellemezzem tulajdonságaikat, különös figyelemmel a kvantumbit-alkalmazásokra.

A SiV-ponthiba negatívan töltött állapotban bizonyítottan kvantumbitként viselkedik, de a spin-pálya kölcsönhatás miatt a kvantumbitműveleteket csak millikelvin hőmérsékleten lehet végrehajtani. Várhatóan a IV. oszlopban lejjebb elhelyezkedő atomok nagyobb spin-pálya kölcsönhatást okoznak, amellyel a kvantumbit működési hőmérsékletét növelni lehetne, ami fontos praktikus szempont a kvantumtechnológiában. Azt tűztem ki célul, hogy a SiV, GeV, SnV, és PbV magnetooptikai paramétereit meghatározzam, különös figyelemmel a kvantumtechnológiai alkalmazásokra.

Módszerek

Atomi szintű szimulációim során az atommagokat álló klasszikus ionoknak feltételeztem (Born-Oppenheimer-közelítés), míg az elektronszerkezetet a sűrűségfunkcionál-elmélet segítségével határoztam meg. Az általam megvizsgált ponthibákat tipikusan 512 szénatomból álló gyémánt szupercellába helyeztem (1. ábra), mely szupercella már elég nagy, hogy elhanyagolhatók legyenek a véges méretű modellezésből fakadó hibák. Az általam felhasznált módszerekkel a ponthibák alábbi fizikai tulajdonságainak feltérképezésére van lehetőség:

●     Atomok egyensúlyi pozíciójának meghatározása. (1–3. ábrák)

●     Elektronszerkezet meghatározása.

●     Magok és elektronok magspinje közötti mágneses dipólus-dipólus kölcsönhatás (hiperfinom kölcsönhatás) modellezése.

●     Elektronszerkezet kölcsönhatása látható fénnyel: optikailag gerjesztett állapotok.
Ponthibák fotolumineszcenciájának és abszorpciójának leírása.

●     Born-Oppenheimer-közelítésen túli módszerek: Jahn-Teller-rendszerek modellezése.

●     Elektronok pályamomentuma és spinje közti kölcsönhatás. (spin-pálya-kölcsönhatás)

 

Az elektronszerkezet-számolásokat a VASP programcsomaggal végeztem, amely jól skálázódik akár több száz vagy több ezer processzormagra, mely számítási kapacitás felhasználásával a több ezer atomból álló rendszer kvantummechanikai viselkedése modellezhető a sűrűségfunkcionál-elmélet segítségével. Saját fejlesztéseket is végeztem, a Born-Oppenheimer-közelítésen túli Jahn-Teller-effektust a Gnu Octave-környezet segítségével modelleztem numerikus számításokkal. A VASP programcsomag módosítása is szükséges volt, hogy a spin-pálya kölcsönhatás által indukált nem sugárzásos (foton kibocsátása nélküli) átmeneteket is modellezni tudjam.

 

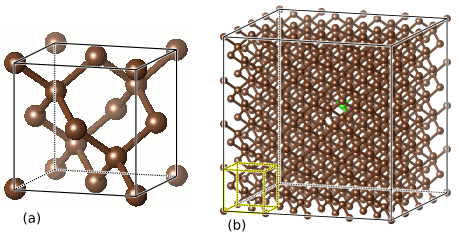
2. ábra: (a) A gyémánt köbös szimmetriáját tükröző Bravais-cellája. (b) Egy NV‑centrumot és 510 szénatomot tartalmazó gyémánt-szupercella. Az ellentétes oldalak a számolások során össze vannak kötve, így a modellezett rendszer egy önmagában végződő határvonallal nem rendelkező 3 dimenziós tórusz

Eddigi eredmények

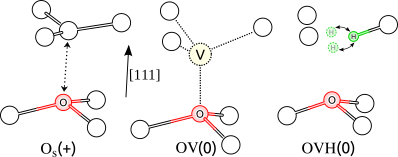
Új, eddig nem modellezett hibacentrumok vizsgálata nagyban hozzájárul további kvantumbit-alternatívák feltérképezéséhez. Ennek érdekében különféle, szilíciumból, hidrogénből, és oxigénből álló eddig azonosítatlan komplexumokat vizsgáltam meg atomi szintű szimulációkkal [T10,T11]. Ilyen komplex a KUL12 címkével jelölt elektron-paramágnesesrezonancia-centrum oxigénnel szennyezett gyémántmintákban, melyről beláttam, hogy a pozitívan töltött O_S(+) ponthibaként azonosítható (2. ábra).

3. ábra: A pozitívan töltött szubsztitúciós oxigén-centrum, semleges oxigén-vakancia és a semleges oxigén-vakancia-hidrogén komplexum. Mindhárom ponthiba paramágnesesen aktív, és 120°-os háromfogású szimmetriát mutat. A kvantummechanikai alagutazás következtében az OVH(0)-centrum hidrogénje az elektron-paramágneses rezonancia (EPR) -mérésekben egyszerre látszik mindhárom szénatomhoz kötve, egyszerűen fogalmazva, folyamatosan “alagutazik”

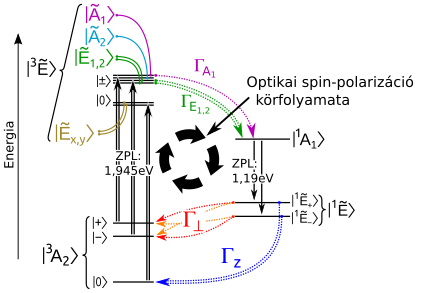
A már kísérletekben megfigyelt ponthibák fizikájának elméleti vizsgálata is fontos feladat. A negatívan töltött NV(-)-centrum spinpolarizációs folyamata alapvető a kvantumtechnológiai alkalmazásokban, mégis a spinpolarizációs folyamat pontos fizikai hátterét eddig még nem értették meg (2. ábra). Modellem alapján beláttam, hogy a nem sugárzásos átmeneteket alapvetően a (pszeudo-) Jahn-Teller-effektus [7] és a spin-pálya- kölcsönhatás együttesen kormányozza [T3,T7], amely végül az S_z=0 alállapot többségi betöltéséhez vezet megvilágítás hatására. Az NV-centrumot többféle töltésállapotban is megfigyelték, melynek modellezése is fontos feladat volt [T6].

4. ábra: Az NV-centrum spinpolarizációs folyamata. A fekete nyilak optikai gerjesztéseket jelölnek (1,945 eV abszorpció és 1,19 eV lumineszcencia), míg a színes pontozott nyilak nem sugárzásos (foton kibocsátása nélküli) átmeneteket. Az 1,945 eV-os átmenetet látható fénnyel aktiválva a körfolyamatot pumpálva még szobahőmérsékleten is elérhető, hogy a |³A₂〉alapállapot |0〉-val jelölt S_z=0 spinű alállapota legyen többségében betöltött. Kutatásaim során a Γ-val jelölt folyamatok modellezésével a kísérletekkel összeegyeztethető modellt állítottam fel, mellyel a spinpolarizáció fizikáját meg lehet magyarázni [T3,T7]

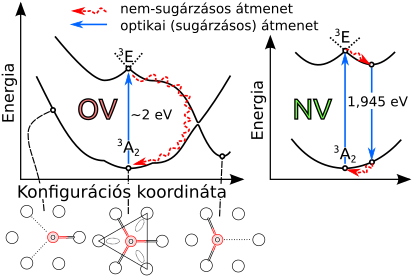
Az elméleti számolások szükségességét jól mutatja az OV(0)-centrum története (3. ábra). Az OV- és NV-ponthibák közös ³A₂ alapállapottal rendelkeznek (izoelektronikusak), a magas S=1 elektronspin mindkét ponthibában megfigyelhető volt EPR-kísérletekben. Emiatt előzetesen azt várták, hogy az OV spinje is polarizálható. A gerjesztett állapotuk azonban alapvetően más (5. ábra), emiatt az OV nem rendelkezhet lumineszcens jellel, sem nem mutathat optikai spinpolarizációt a kísérleti tényekkel egyezésben [T10].

5. ábra: Az oxigén-vakancia centrum nem sugárzásos relaxációs útja. Amíg az NV fotont elnyelni és kibocsátani is képes, addig az OV-centrum csak elnyelni. Az OV esetében az egyik C–O kötés felszakításával NV-centrumra nem jellemző folyamat indul be

Kutatásaim során részletesen megvizsgáltam a SiV(-), GeV(-), SnV(-), PbV(-) ponthibák magnetooptikai tulajdonságait [T1,T4,T5]. Eredményeim alapján meghatároztam a Ham[8]- és Stevens[9]-féle redukciós faktorok hatását az optikai spektrumokban észlelhető spin-pálya kölcsönhatásra, mely segítségével kvantumbit állapota manipulálható.

Várható impakt, további kutatás

A kvantumtechnológiai kutatásokban az egyik legfontosabb irány új szilárdtestbeli kvantumbitek felfedezése, amelyeket szuperérzékeny érzékelők létrehozásában [10,11,12], kvantuminformáció jeltovábbításának területén, vagy éppen biológiai jelzőrendszerként az orvostudományokban is tudnak a jövőben hasznosítani [12]. Ebben a kutatásban az atomi szintű, nagy pontosságú szimulációs módszerek fontos szerepet játszanak, amelyekkel meg lehet jósolni új kvantumbiteket, vagy az ismert kvantumbitek pontos működését fejthetik meg, ami segíthet a működésük optimalizációjában. Eredményeim a gyémántbeli kvantumbitek felfedezéséhez és működéséhez járul hozzá, illetve módszert ad arra, hogy más anyagokban ezt sikerrel meg lehessen valósítani.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája:

(IP, impakt faktor)

[T1] G. Thiering, A. Gali, Ab initio magneto-optical spectrum of group-IV-vacancy color centers in diamond.  Phys. Rev. X 8, 021063 (2018) IP: 12.789

[T2] B. Rose, G. Thiering,… A. Gali, S. Lyon, N. de Leon: Strongly anisotropic spin relaxation in the neutral silicon vacancy center in diamond e-print arXiv:, quant-ph/1702.01590.

[T3] G. Thiering, A. Gali: Theory on the optical spinpolarization loop of the nitrogen-vacancy center in diamond  e-print arXiv: quant-ph/1803.02561.

[T4] E. Londero, G. Thiering, A. Gali, A. Alkauskas: e-print arXiv:, quant-ph/1605.02955. Vibrational modes of negatively charged silicon-vacancy centers in diamond from ab initio calculations.

[T5] Häußler S, Thiering G, Dietrich A, Waasem N, Teraji T, Isoya J, Iwasaki T, Hatano M, Jelezko F, Gali A, Kubanek A: Photoluminescence excitation spectroscopy of SiV(-) and GeV(-) color center in diamond New Journal of Physics 19:(6) Paper 063036. 9 p. (2017) IP: 3.786

[T6] Pfender M, Aslam N, Simon P, Antonov D, Thiering G, Burk S, Favaro de Oliveira F, Denisenko A, Fedder H, Meijer J, Garrido JA, Gali A, Teraji T, Isoya J, Doherty MW, Alkauskas A, Gallo A, Gruneis A, Neumann P, Wrachtrup J: Protecting a Diamond Quantum Memory by Charge State Control Nano Letters 17:(10) pp. 5931–5937. (2017) IP: 12.712

[T7] Thiering G, Gali A: Ab initio calculation of spin-orbit coupling for an NV center in diamond exhibiting dynamic Jahn-Teller effect Phys. Rev. B 96:(8) Paper 081115. 6 p. (2017) IP: 3.836

[T8] Udvarhelyi P, Thiering G, Londero E, Gali A: Ab initio theory of the N2V defect in diamond for quantum memory implementation Phys. Rev. B 96:(15) Paper 155211. 7 p. (2017) IP: 3.836

[T9] Gali A, Demján T, Vörös M, Thiering G, Cannuccia E, Marini A: Electron-vibration coupling induced renormalization in the photoemission spectrum of diamondoids Nat. Comm. 7: Paper 11327. 9 p. (2016) IP: 12.124

[T10] Thiering G, Gali: A Characterization of oxygen defects in diamond by means of density functional theory calculations Phys. Rev. B 94:(12) Paper 125202. 15 p. (2016) IP: 3.836

[T11] Thiering G, Gali A: Complexes of silicon, vacancy, and hydrogen in diamond: A density functional study Phys. Rev. B 92:(16) Paper 165203. 15 p. (2015) IP: 3.718

[T12] Thiering G, Londero E, Gali: A Single nickel-related defects in molecular-sized nanodiamonds for multicolor bioimaging: an ab-initio study Nanoscale 6: pp. 12018–12025. (2014) IP: 7.394

 

Linkgyűjtemény:

 

Dr. Gali Ádám kutatócsoportja:

http://www.fat.bme.hu/kulonc/galia/

https://wiki.kfki.hu/nano

Wikipédia oldalak:

https://hu.wikipedia.org/wiki/Kvantumbit

https://hu.wikipedia.org/wiki/Jahn-Teller-effektus

Egyéb:

A kvantumkémia alapjai és alkalmazása

https://wiki.kfki.hu/nano/Defects_for_quantum_information_processing

https://wiki.kfki.hu/nano/Defect_Identification

 

Hivatkozások listája:

                                   

[1] J. R. Weber, W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. Van de Walle, and D. D. Awschalom: Quantum computing with defects - Proceedings of the National Academy of Sciences 107 19, 8513–8518 (2010)

[2] Doherty, M. W., Manson, N. B., Delaney, P., Jelezko, F., Wrachtrup, J., & Hollenberg, L. C. (2013). The nitrogen-vacancy colour centre in diamond. Physics Reports, 528(1), 1–45.            

[3] Sukachev, D. D., Sipahigil, A., Nguyen, C. T., Bhaskar, M. K., Evans, R. E., Jelezko, F., & Lukin, M. D. (2017). Silicon-Vacancy Spin Qubit in Diamond: A Quantum Memory Exceeding 10 ms with Single-Shot State Readout. Physical review letters, 119(22), 223602.

[4] Bhaskar, M. K., Sukachev, D. D., Sipahigil, A., Evans, R. E., Burek, M. J., Nguyen, C. T., ... & Jelezko, F. (2017). Quantum nonlinear optics with a germanium-vacancy color center in a nanoscale diamond waveguide. Physical review letters, 118(22), 223603.

[5] Tchernij, S. D., Herzig, T., Forneris, J., Küpper, J., Pezzagna, S., Traina, P... & Genovese, M. (2017). Single-photon-emitting optical centers in diamond fabricated upon Sn implantation. ACS Photonics, 4(10), 2580–2586.

[6] Goldman, M. L., Sipahigil, A., Doherty, M. W., Yao, N. Y., Bennett, S. D., Markham, M., ... & Lukin, M. D. (2015). Phonon-induced population dynamics and intersystem crossing in nitrogen-vacancy centers. Physical review letters, 114(14), 145502.

[7] Bersuker, I. (2013). The Jahn-Teller effect and vibronic interactions in modern chemistry. Springer Science & Business Media.

[8] Ham, F. S. (1965). Dynamical Jahn-Teller effect in paramagnetic resonance spectra: orbital reduction factors and partial quenching of spin-orbit interaction. Physical Review, 138(6A), A1727.

[9] Stevens, K. W. H., & Pryce, M. H. L. (1953). On the magnetic properties of covalent XY 6 complexes. Proc. R. Soc. Lond. A, 219(1139), 542–555.

[10] Maletinsky, P., Hong, S., Grinolds, M. S., Hausmann, B., Lukin, M. D., Walsworth, R. L., ... & Yacoby, A. (2012). A robust scanning diamond sensor for nanoscale imaging with single nitrogen-vacancy centres. Nature nanotechnology, 7(5), 320.

[11] Dolde, F., Fedder, H., Doherty, M. W., Nöbauer, T., Rempp, F., Balasubramanian, G.,... & Wrachtrup, J. (2011). Electric-field sensing using single diamond spins. Nature Physics, 7(6), 459.

[12] Kucsko, G., Maurer, P. C., Yao, N. Y., Kubo, M. I. C. H. A. E. L., Noh, H. J., Lo, P. K., ... & Lukin, M. D. (2013). Nanometre-scale thermometry in a living cell. Nature, 500(7460), 54.