Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék

Témavezető: Dr. Insperger Tamás

Regeneratív szerszámgéprezgés robusztus stabilitása és szabályozása

A kutatási téma néhány soros bemutatása

A regeneratív szerszámgéprezgés olyan dinamikai jelenség, amely a nem abrazív forgácsolási folyamat során nemkívánatos nagyamplitúdójú rezgésekhez (1. ábra) és ezáltal rossz felületi minőséghez vezet. A kutatás témája a jelenséget kialakító körülmények vizsgálata, a rezgés megszűntetése, valamint a jelenlegi modellek pontosítása a folyamatot terhelő bizonytalanságok figyelembevételével.

 

 

1. ábra: Marási folyamat gyorskamerás felvétele (8400 fordulat/perc)

 

A kutatóhely rövid bemutatása

A SIREN ERC kutatócsoport 2013-ban alakult az Európai Kutatási Tanács (European Research Council) támogatásával ötéves időszakra. Megalakulásakor három kutatócsoport kezdte meg munkáját, melyeknek célja a forgácsleválasztás pontosabb modellezése, a szerszámgép elemei közötti mechanikai kapcsolatok vizsgálata és a főorsó dinamikájának pontosabb megismerése.

 

A kutatás történetének, tágabb kontextusának bemutatása

A szerszámgéprezgés jelentőségének felismerése a XX. század elejére tehető, az első pontosabb matematikai modellek azonban csak jóval később, az 1960-as években jelentek meg [H1,H2]. Ezek a modellek a technikai korlátok miatt még egyszerűbb számításokra korlátozódtak, azonban a modern számítógép megjelenésével és a technológia fejlődésével lehetőség nyílt a jelenség mélyebb tanulmányozására. Mára a kutatás eredményeképpen számos matematikai módszert dolgoztak ki a rezgések előrejelzésére, de jelentős mennyiségű mérnöki megoldás is született annak megszüntetésére, például az aktív és passzív rezgéscsillapítók [H3].

 

A jelenség felismeréséhez és elkerüléséhez annak pontos megértése szükséges. Ahogy az 1. ábrán is látható, a forgácsolás során belépő szerszámok periodikusan gerjesztik a munkadarabot (fordítva a szerszámot is), és így a fordulatszámtól függően felületi hibát hoznak létre. Mivel a felület megőrzi a rezgés hatását, így fordulatonként megváltozik a leválasztandó forgács geometriája, ami egy múltbéli rezgés hatásától függő forgácsolási erőt hoz létre. Ezt nevezzük regeneratív hatásnak, melyet időben periodikus és késleltetett differenciálegyenletek írnak le. Ilyen típusú rendszereknél létrejöhet stabilitásvesztés, mely során egyre növekvő rezgés amplitúdó jelentkezik, egészen addig, amíg a szerszám élei el nem veszítik a kapcsolatot a munkadarabbal, és durva felületi hibát nem eredményeznek. Ezt a jelenséget nevezzük chatternek, mely nemcsak a felületre káros, de csökkenti a szerszám élettartamát, és akár szerszámtöréshez vagy egyéb tönkremenetelhez is vezethet.

 

A kutatás célja, a megválaszolandó kérdések.

Megmunkálási folyamatoknál a dinamikai méréseket követően lehetőség van úgynevezett stabilitási diagramok számítására, amely elhatárolja egymástól azokat a technológiai tartományokat (a fordulatszám és fogásmélység függvényében), melyek esetén jelentkezik, vagy nem jelentkezik ilyen típusú öngerjesztett rezgés, azaz chatter. A számításokhoz szükség van a szerszámgép dinamikájának pontos ismeretére és a forgácsleválasztási folyamat megfelelő modelljére is [H4]. Ezeket a paramétereket előzetes mérésekből határozhatjuk meg: a modális paramétereket például impulzuskalapáccsal történő gerjesztéssel, a forgácsolási erőegyütthatókat pedig forgácsolási tesztekkel. Matematikai módszerekkel számíthatók ezek a diagramok (ld. 4. ábra) [H5].

 

A mérések azonban jellemzően nem teljesen pontosak, az illesztések hibákat tartalmaznak [K1,K2,F4], és a kiinduló modellek is gyakran tapasztalati vagy egyszerűsített összefüggéseken alapszanak. Így gyakran a kísérletek sem tükrözik az elméleti számításokat, ami gátat szab az eredmények ipari célra történő felhasználásának [F3].

 

A módszerek javítása érdekében figyelembe kell venni a modellezés bizonytalanságait is. Azokat a rendszereket, amelyek a becsült bizonytalanság ellenére is az elvárt követelményeknek megfelelően működnek, robusztusnak nevezzük. A kutatás célja olyan módszer kialakítása, mellyel garantálható az instabil rezgések elkerülése, és ily módon biztosítható a stabil megmunkálás, valamint a jó felületi minőség.

 

Módszerek

Eddigi kutatásaink, valamint szakirodalmi hivatkozások alapján úgy találtuk, hogy a modális paraméterek meghatározása jelentős bizonytalansággal terhelt [F4]. Az irodalomban fellelhető módszerek túlnyomó többsége nem alkalmazható hatékonyan e paraméterekre vetített robusztusság meghatározására, ugyanis a számítási igény túlságosan nagy, sőt gyakran teljesen kivitelezhetetlen [F1,K3]. A problémát az is súlyosbítja, hogy a szakirodalomban nem létezik olyan módszer, amellyel időben késleltetett periodikus együtthatójú rendszer egyenleteinek robusztus stabilitása jól vizsgálható.

 

Multi-frekvencia módszer

 

A probléma áthidalására a frekvenciaátviteli függvények bizonytalanságait használtuk fel, modális paraméterek illesztése nélkül [F1,F2,K3]. Ily módon közvetlenül meghatározható ütési kísérletekből a mérés bizonytalansága (normális eloszlás vagy alsó-felső burkoló számításával is). Egy ilyen mért frekvenciaátviteli mátrix elemeit mutatja a 2. ábra tíz darab egyedüli ütési kísérlet (szürke) és azok átlaga (fekete) alapján. Láthatóan pontatlan a mérés, így azok átlaga sem elegendő a valós dinamika pontos leírására. A szakirodalomban létező multi-frekvencia módszer [H4,H6] közvetlenül a mért átviteli függvények alapján határozza meg a stabilitási tartományokat, azonban ez a módszer nem képes a bizonytalanság figyelembevételére.

 

 

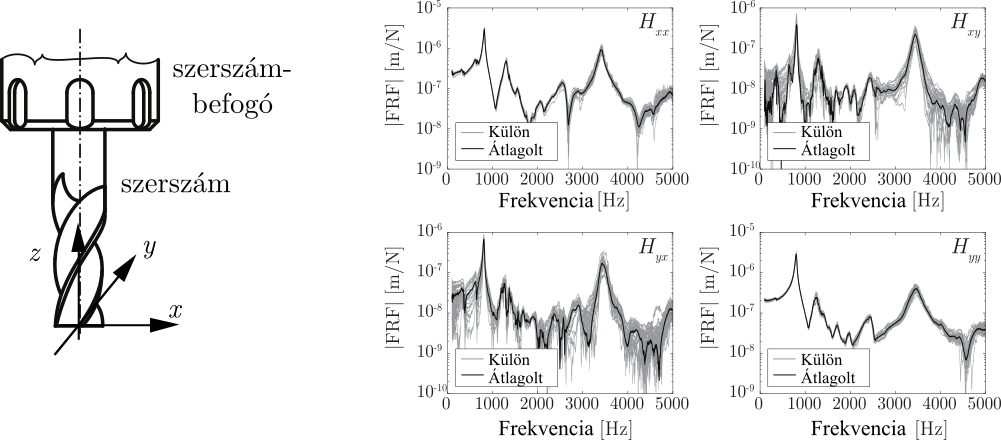
2. ábra: Szerszámcsúcs mért frekvenciaátviteli mátrixa (különálló és átlagolt mérés)

 

Strukturált szingulár sajátérték vizsgálat

 

A bizonytalanság figyelembevételére a strukturált szinguláris sajátérték analízist (mu-analízis) találtam legmegfelelőbbnek [H7], mely a robusztus irányítások elméletében gyakran alkalmazott módszer. A dinamikai modell egyenleteit az M-Delta bizonytalansági struktúrával írhatjuk fel, mely magában foglalja a frekvenciaátviteli függvények hibáját is. A multi-frekvencia módszer és az említett robusztus módszer kombinálásával olyan számítási módszert kapunk, mellyel már közvetlenül számíthatók a biztonságos stabilitási határok [F2,K4].

 

A standard módszer azonban így sem bizonyult a számítási idő szempontjából kellően gyorsnak, de egy enyhén konzervatív közelítéssel élhetünk a számítás során, amelyet a [H8] szakirodalom mutat be. Így jelentősen gyorsítható a számítás, a robusztus stabilitási határok pedig időben nagyságrendileg az átlagolt rendszer stabilitási határaival együtt számíthatók [F2].

 

Eddigi eredmények

 

Kísérlet - Marási folyamatok robusztus stabilitásvizsgálata

 

A 3. ábra a kísérleti összeállítást mutatja, valamint a jobb oldalon egy instabil és egy stabil megmunkálás után keletkező felületdarab látható. A kísérlet egy kétélű, reguláris szerszámmal történt, a megmunkálás során 50%-os egyenirányú marást végeztünk.

 

 

3. ábra: Kísérleti összeállítás [K4]

 

Az eredményeket a 4. ábra mutatja, ahol az elméleti számításokat a mérésekkel hasonlítottuk össze. A szerszámcsúcshoz tartozó átviteli mátrix elemeit és bizonytalanságát az 5. ábra mutatja. A 4. ábra (a) diagramja a számított berezgési frekvenciákat, míg (b) diagramja a robusztus stabilitási térképet ábrázolja. A robusztus tartomány számításának szükségességét jól indokolja a mérés és az elmélet közötti kisebb-nagyobb eltérés. A kísérletben tapasztalt berezgési frekvenciák a fordulatszám növelésével egyre inkább eltérnek az elméleti eredménytől, ami jelzi a dinamikai tulajdonságok frekvenciafüggését. A stabilitási térképen is látható, hogy a mérési eredmények kissé eltérnek az átlagos rendszerhez tartozó határoktól (fekete görbe), de a robusztusan stabil tartomány (piros görbe alatti sötétszürke terület) szinte csak stabil pontokat foglal magában.

 

 

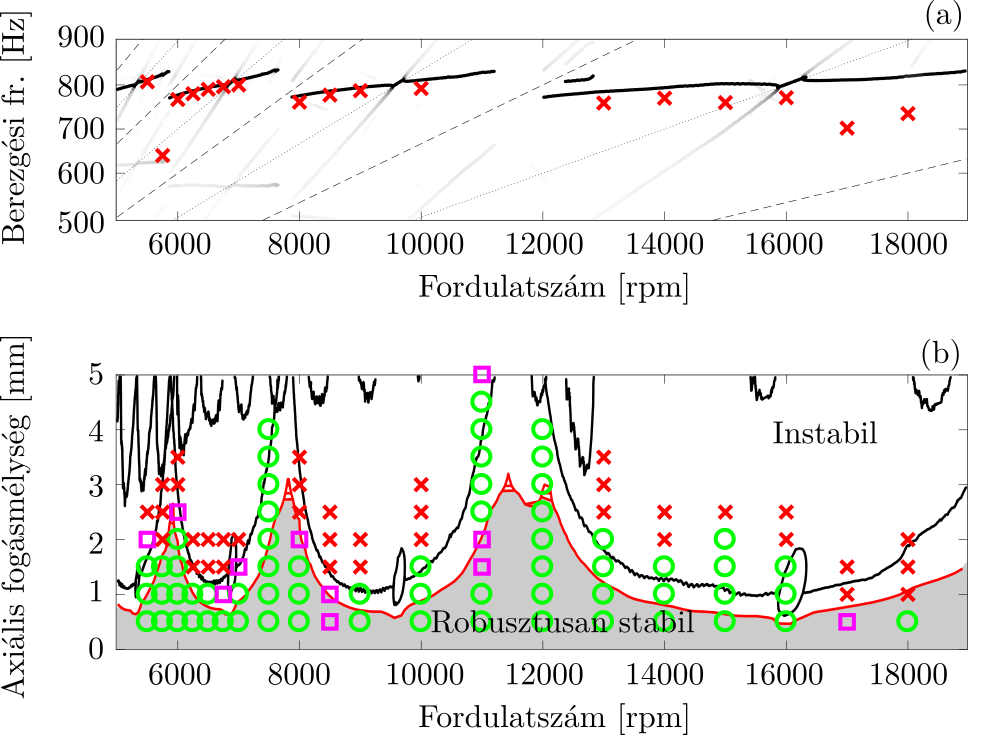
4. ábra: Mért és robusztus stabilitási diagramok: (a) Berezgési frekvenciák (b) Robusztus stabilitási diagram (Mérési pontok: zöld kör - stabil, magenta négyzet - határ, piros kereszt - instabil) [K4]

 

Tanulmány - Robusztus szabályozó tervezése esztergálási folyamatokhoz

 

Az eredmények továbbfejleszthetők robusztus aktív és passzív csillapítók tervezéséhez is. Az esztergálási folyamatok (5. ábra) során kialakuló rezgések aktív lengésfolytóval történő csillapítása esetén a szabályozó hangolása függ a rendszerben jelenlévő időkésésektől, valamint a beavatkozó pont és szerszámcsúcs közti frekvenciaátviteli mátrix bizonytalanságától [K5]. A 6. ábrán animált videó mutatja, hogy egy robusztusan hangolt PD szabályozó mellett (sötétszürke tartomány) jelentősen növelhető a stabil tartomány, szemben a nem robusztus szabályozóval (világosszürke tartomány), ahol a bizonytalansági zóna összemérhető a robusztus tartománnyal.

 

        

 

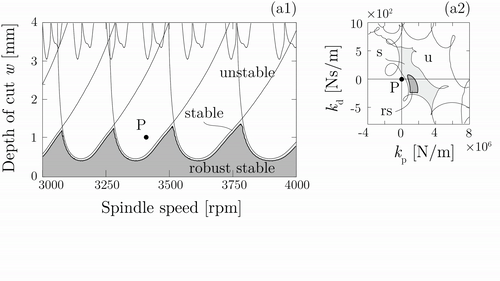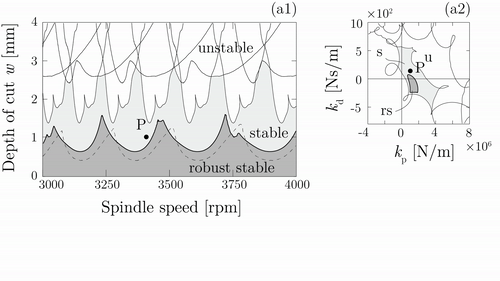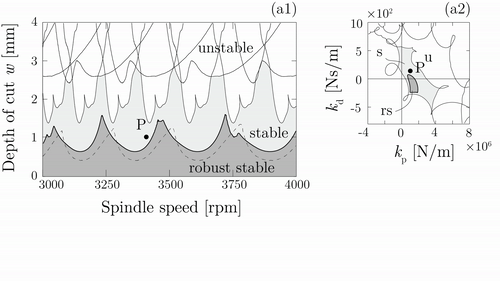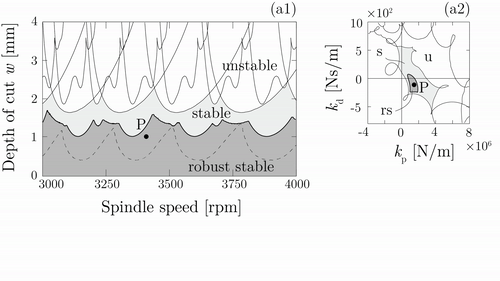
5. ábra: Esztergálási folyamatok modellje aktív lengésfolytóval. (Három különböző eset: I. szabályozó nélkül, II. nem robusztus szabályozó, III. robusztus szabályozó) [K5]

 

Várható impakt, további kutatás

A kísérleti eredmények és tapasztalatok jól mutatják a robusztus stabilitás számítási módszereinek szükségességét megmunkálási folyamatok esetén. A kidolgozott módszer előnye a gyors számítás és könnyű programozhatóság, ami alkalmazhatóvá teszi azt ipari vagy iparhoz közeli alkalmazások bevezetésében. Várhatóan az elméleti modellek terjedésével a robusztus számítási módszerek iránti igény is tovább fog növekedni.

 

További kutatásokban potenciált jelenthet a módszer konzervativitásának csökkentése, illetve a robusztus szabályozó tervezésének kiterjesztése esztergálási folyamatokról marási folyamatokra.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Folyóiratcikkek

[F1]  D. Hajdu, T. Insperger, Gábor Stépán, Robust stability analysis of machining operations, The International Journal of Advanced Manufacturing Technology, 2017.
IF = 2.209 (2016)

[F2] D. Hajdu, T. Insperger, D. Bachrathy, G. Stepan, Prediction of robust stability boundaries for milling operations with extended multi-frequency solution and structured singular values, Journal of Manufacturing Processes 30:281–289, 2017.

IF = 2.322 (2016)

[F3] A. K. Kiss, D. Hajdu, D. Bachrathy, G. Stepan, Operational stability prediction in milling based on impact tests, Mechanical Systems and Signal Processing, 103:327–339, 2018.

IF = 4.116 (2016)

[F4] G. Stepan, D. Hajdu, A. Iglesias, D. Takacs, Z. Dombovari, Ultimate capability of variable pitch milling cutters, CIRP Annals, In press, 2018.

IF = 3.333 (2017)

Konferenciacikkek

[K1] D. Hajdu, T. Insperger, G. Stépán, Sensitivity of stability charts with respect to modal parameter uncertainties for turning operations, 12th IFAC Workshop TDS, Ann Arbor, MI, USA, 2015.

[K2] D. Hajdu, T. Insperger, G. Stépán, The effect of non-symmetric FRF on Machining: A Case Study, ASME IDETC, Boston, MA, USA, 2015.

[K3] D. Hajdu, T. Insperger, G. Stépán, Robust Stability of Machining Operations in Case of Uncertain Frequency Response Functions, 7th HPC 2016 – CIRP HPC, Chemnitz, Németország, 2016.

[K4] D. Hajdu, T. Insperger, G. Stépán, Quantification of uncertainty in machining operations based on probabilistic and robust approaches, 8th HPC 2018 – CIRP HPC, Budapest, Magyarország, 2018.

[K5] D. Hajdu, T. Insperger, G. Stepan, Robust controller design for turning operations based on measured frequency response functions, 20th World Congress of the International Federation of Automatic Control, Toulouse, 2017.

 

Linkgyűjtemény

SIREN - Stability Islands: Performance Revolution

SIREN ERC Project: Stable down-milling @7675 rpm (Készítette: Hajdu Dávid)

SIREN ERC Project: Stable down-milling @ 8000 rpm (Készítette: Hajdu Dávid)

SIREN ERC Project: Unstable down-milling @ 8400 rpm (Készítette: Hajdu Dávid)

 

Hivatkozások listája.

[H1] Tobias, S. Machine-tool Vibration. Glasgow: Blackie, 1965.

[H2] Tlusty, J., Spacek, L. Self-excited vibrations on machine tools. Prága. Cseh nyelven: Nakl. CSAV, 1954.

[H3] J. Munoa, X. Beudaert, Z. Dombovari, Y. Altintas, E. Budak, C. Brecher, G. Stepan,

Chatter suppression techniques in metal cutting, CIRP Annals, 65(2):785–808, 2016

[H4] E. Budak, Y. Altintas, Analytical prediction of chatter stability in milling, part I: General formulation, J Dyn SystT ASME 120:22–30, 1998.

[H5] T. Insperger, G. Stepan, Semi-discretization for time-delay systems, 178, Springer, New York, 2011.

[H6] Bachrathy, D., Stepan, G. Improved prediction of stability lobes with extended multi frequency solution. CIRP Annals 62(1):411–414, 2013.

[H7] J. Doyle, Analysis of feedback systems with structured uncertainties, IEE Proc. Part D. 129:242–250., 1982

[H8] M. Karow, D. Hinrichsen, A. J. Pritchard, Interconnected systems with uncertain couplings: explicit formulae for -values, spectral value sets and stability radii, SIAM Journal on Control and Optimization 45(3):856–884, 2006.