Villamosmérnöki Tudományok  Doktori Iskola 

BME-VIK, Villamos Energetika Tanszék

Témavezető: Dr. Tamus Zoltán Ádám

Nagytranszformátorok szigetelési rendszerének költségoptimalizálása

A kutatási téma néhány soros bemutatása

Nagytranszformátorok tervezése összetett, multidiszciplináris feladat, ahol a leggazdaságosabb design paramétereinek a megválasztása során, egyszerre kell számos mechanikai, villamos és termikus igénybevételt, előírást figyelembe venni [1,2].

Ennek a feladatnak a megoldása a legáltalánosabb matematikai optimalizálási problémák családjába tartozik. A gyakorlatban a tervezést több szakaszra bontják; kutatásom során az első, előzetes vagy ajánlati tervezési szakasszal foglalkozom, amelynek a célja, az előírásoknak és az igénybevételeknek megfelelő költség-optimális konstrukció főméreteinek [3,4] a meghatározása egy egyszerűsített modell segítségével (1. ábra).

 

 

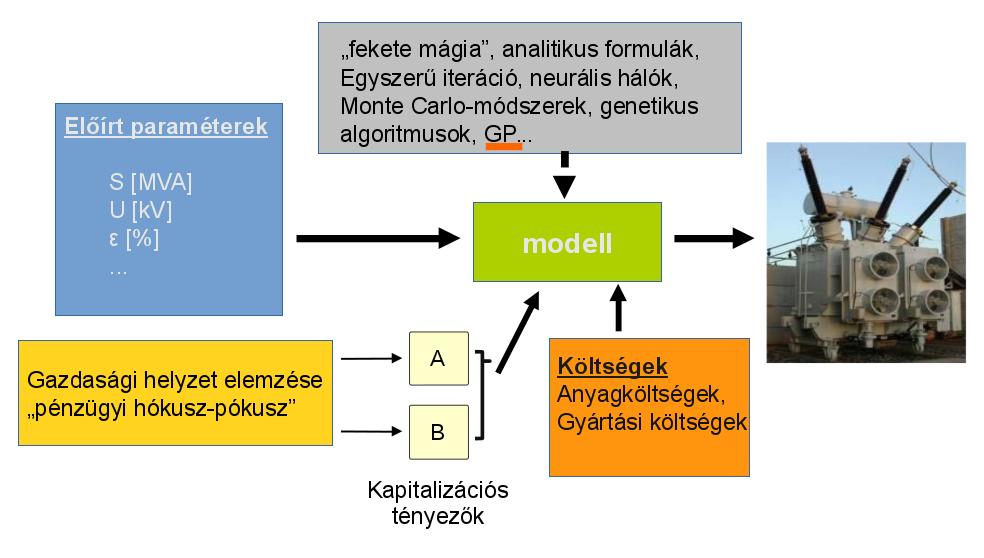
1. ábra: Az előzetes tervezés optimalizálási feladata

A kutatóhely rövid bemutatása                                          

Kutatómunkámat a BME Villamos Energetika Tanszékén végzem, együttműködve hazai és külföldi partnerekkel. A tanszék, az egyetem első villamosmérnöki tanszékeként 1893-ban alakult meg Zipernowsky Károly, a zárt vasmagos transzformátor egyik feltalálójának a vezetésével. A tanszék legfőbb küldetése, hogy az ipar jó együttműködő partnere legyen mérnökök képzésében, és folyamatosan együttműködik számos európai és a tengerentúli egyetemmel, folyamatosan szervez konferenciákat és szakképzéseket.

 

A kutatás történetének, tágabb kontextusának bemutatása                                    

Az adott gazdasági környezethez jól illeszkedő, költség-optimális nagytranszformátor-konstrukció főméreteinek a meghatározása bonyolult feladat, amely a legáltalánosabb matematikai optimalizálási problémák családjába tartozik. A folyamat egyszerűsítése érdekében a tervezés folyamatát több, a klasszikus villamos gép-tervezői megközelítés szerint 3 szakaszra bontják [3]:

 

●     Előzetes vagy ajánlati tervezési szakasz, amely során egy egyszerűsített modellen keresztül határozzák meg az előírásoknak és az igénybevételeknek megfelelő költség-optimális konstrukció fő tervezési paramétereit.

 

●     Végleges tervezési szakasz, amely az előzetes tervezésben kapott, fő tervezési paraméterek által meghatározott terv teljes részletességgel való kidolgozása.

                                         

●     Ellenőrzési szakasz.

 

                                               

A kutatásom során kizárólag az előzetes tervezési szakaszhoz tartozó optimalizálási problémákkal foglalkoztam. Az ajánlati tervezési szakasznak az a kulcsproblémája, hogy nagyon rövid idő alatt kell egy nemcsak technikai, hanem gazdaságossági szempontoknak is megfelelő, versenyképes transzformátor kulcsparamétereit megtalálni. Ennek a feladatnak a nyers erővel való megoldása rendkívül számításigényes. Ahogy [3]-ban látható, már egy ennél jóval egyszerűbb, három feltételt tartalmazó, standard elemekkel dolgozó, idealizált esetben is nagyságrendileg 100 000 lehetséges változat közül kell az optimálist megtalálnia a tervezőnek.

 

A téma fontosságát jelzi, hogy az első analitikus módszerek már alig több mint egy évtizeddel a zárt vasmagos transzformátorok feltalálása után megszülettek [4]. Ezek az optimumszámító eljárások jellemzően rengeteg egyszerűsítést, technológiafüggő konstanst tartalmaztak, így használhatóságuk meglehetősen korlátozott, és használatuk rossz szerkesztési irányelvek megszületéséhez vezetett [4,6]. Az 50-es évektől kezdődően napjainkig, a számítógépek megjelenésével számtalan algoritmust fejlesztettek a főméretek meghatározására. Ezek a programok az egyszerű iterációtól kezdve a legkülönfélébb numerikus és matematikai programozási, mesterséges intelligencián alapuló módszereket alkalmazzák ennek az optimalizálási folyamatnak a minél gyorsabb és pontosabb megoldására [7, 8].

 

Ezeket az előzetes tervezéshez kapcsolódó módszereket többféle célfüggvénnyel lehet definiálni: gyártási költség minimalizálása, össztömeg minimalizálása, befoglaló méretek minimalizálása, hatásfok maximalizálása, stb. Munkám során a teljes életútköltségre való optimalizálással foglalkoztam, amely, úgynevezett kapitalizációs tényezőkön keresztül figyelembe veszi a gép gyártási költsége mellett az élettartama során keletkező egyéb költségeket is [7]. Az élettartamköltségekre való optimalizálás iránti igény már a XX. század elején megjelent. Az erőátviteli transzformátor-gyártás úttörőjének számító Ganz gyárban, különböző réz- és vasveszteség-aránnyal készítettek transzformátorokat víz- és gőzturbinákhoz, így véve figyelembe az eltérő terhelési jellemzőket. Napjainkban már sokkal kifinomultabb módszerek léteznek a különböző költségek figyelembevételére [9, 10].

 

A kutatás célja, a megválaszolandó kérdések.                              

A nagytranszformátorok költség-optimális paramétereinek a meghatározása a legáltalánosabb nem-lineáris matematikai optimalizálási feladatok köréhez tartozik. A feladat bonyolultsága és fontossága miatt számos, különböző egyszerűsítéseket tartalmazó modellt publikáltak, melyek sokszor rossz szerkesztési szokások kialakulásához vezettek. A transzformátorok kulcsparamétereinek meghatározása, a vasmag és a tekercselés méret- és súlyarányainak, valamint igénybevételeinek helyes megválasztásával lehetséges. Ezért ezek az egyszerűsített modellek általában csak a transzformátor tekercsrendszerét és vasmagját tartalmazó (úgynevezett aktív) részével foglalkoznak. Az általánosan elterjedt gyakorlat szerint elhanyagolják a szigetelési és a külső hűtőrendszer főméretekre gyakorolt hatását, illetve a minimális szigetelési távolság alkalmazásával próbálják megtalálni a költség-optimális megoldást. Kutatásom során azt vizsgálom, hogy ezeknek az elhanyagolásoknak, tervezési irányelveknek az előírt nem-lineáris paramétereken keresztül milyen hatása van a transzformátorok főméreteire.

 

 

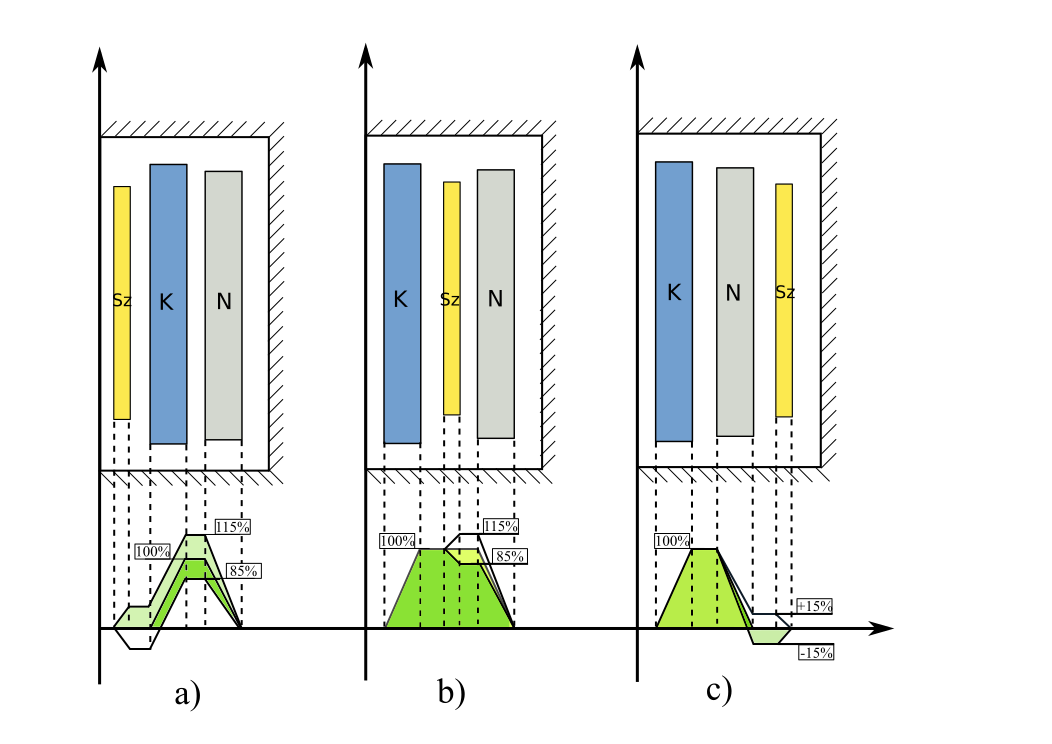
2. ábra: Szabályozótekercs különböző pozíciójának a hatása a gerjesztési képre. K a kisfeszültségű tekercs, N a nagyfeszültségű tekercs, Sz pedig a szabályozótekercset jelöli.

Módszerek                                     

A kutatásom kiindulópontja egy geometriai programozáson alapuló transzformátoroptimalizáló program volt [1, 12]. Ennek a matematikai optimalizálási feladatnak az alkalmazása azért érdekes, mert az újonnan kifejlesztett megoldó módszereknek köszönhetően már nagyon nagyméretű geometriai programozási feladat is pontosan és rövid idő alatt megoldható egy átlagos asztali számítógépen [11]. Továbbá, a formalizmus alkalmazása garantálja, hogy a megtalált optimum a globális optimum lesz.

Ez a módszer azonban kissé hibás eredményeket szolgáltatott mag-típusú transzformátorok esetén: magasabb tekercseket, illetve ablakmagasságot számolt, mint ami a pontosabb számításokból következett volna. Az iparban az a magyarázat elfogadott, hogy a transzformátor szabályozó tekercseihez, vagy egyéb, a szigetelési, illetve hűtőrendszerhez kapcsolódó elhanyagolások okozzák ezt a számítási hibát. Sikerült belátni [C1],[J1], hogy az eltérést az okozza, hogy mag-típusú nagytranszformátorok esetén a rövidzárási impedanciára nem írható fel alsó korlát a geometriai programozás által megkövetelt pozionomiális alakban. Ennek a problémának a kiküszöbölésére létrehoztam a geometriai programozás és a „branch and bound” algoritmusok kombinálásával egy olyan transzformátor-optimalizáló módszert, amely korrigálja a rövidzárási impedancia számítását, továbbá gyors és pontos eredményt szolgáltat. A módszert az irodalomban fellelhető más módszerekkel összevetettem, alkalmazhatóságát igazoltam. A kapott eredményeket az iparban használt végeselemes szoftver segítségével validáltam [14].

Ezzel a módszerrel megvizsgáltam, hogy miként függnek az optimális főméretek a rövidzárási impedanciát befolyásoló szabályozótekercs-elrendezésektől, a szabályozótekercs típusától, a külső hűtőrendszer megválasztásától.

 

Eddigi eredmények                                   

A bemutatott metaheurisztikus modellemet kiegészítettem, hogy a szigetelési- és hűtőrendszer tömegének, költségének a visszahatását megvizsgálhassam természetes olajáramlással hűtött (ONAN/ONAF) transzformátor esetén. Ehhez a vizsgálathoz az előzőekben kifejlesztett metaheurisztikus optimalizáló módszert továbbfejlesztettem, és új paraméterekkel, továbbá a transzformátor külső hűtését leíró hőtani modellel egészítettem ki. Az így továbbfejlesztett optimalizáló módszer segítségével megvizsgáltam, hogy milyen hatása van a nagytranszformátor modell vizsgált paramétereire, ha a kapitalizált árra való optimalizálás során nem hanyagoljuk el az olaj és a külső hűtőrendszer költségét. Azt találtam, hogy a piaci árakhoz képest nagy kapitalizációs tényezők esetén a hűtőrendszer költsége – a tapasztalatoknak megfelelően – nem jelentős. Ennek ellenére, kis kapitalizációs tényezők esetén, amikor az optimális transzformátor konstrukció viszonylag nagy veszteségű lesz, a hűtőrendszer költsége jelentősen befolyásolja a tekercsek menetfeszültségét, ezen keresztül a réz-vas arányt.

 

Az autotranszformátorok beépített teljesítménye kisebb a látszólagos teljesítményénél, ezért a leggazdaságosabb konstrukciót jellemzően nem akkor kapjuk, amikor a szabályozótekercs a két főtekercs után helyezkedik el, minimális hatást gyakorolva a rövidzárási impedancia értékére, hanem amikor a két főtekercs között vagy a kisfeszültségű tekercs és a vasmag között helyezkedik el a szabályozótekercs, hiszen így a tekercselrendezés geometriájánál fogva megnő a drop értéke (2. ábra). A geometriai programozás és a „branch and bound” módszer ötvözésével fejlesztett metaheurisztikus módszer már képes mag-típusú autotranszformátorok esetére is helyesen számítani a drop értékét, így ezekben a különféle elrendezésekben is megtalálja a feladat globális optimumát.

 

A kiegészített metaheurisztikus optimalizáló módszer segítségével megvizsgáltam, hogy a nagytranszformátorok szabályozótekercs típusának (lineáris, durva- finom, irányváltós) [13] a megválasztása milyen hatással van a transzformátor költség-optimális paramétereire. Az irányváltós szabályozás nagy előnyének tartják a durva-finom szabályozással szemben, hogy képes nagy szabályozási tartományt átfogni, további szabályozó tekercs és szigetelés beépítése nélkül, így csökkentve a költségeket. A durva- finom szabályozáshoz kapcsolt előnyöktől eltekintve: egyenletesebb drop-változás a szabályzási tartományban, olcsóbb hűtőrendszertől [13], a rövidzárási impedanciára gyakorolt eltérő hatásukat vizsgálva beláttam, hogy adott gazdasági modell esetén létezik olyan rövidzárási impedancia érték, amely felett a több tekercset tartalmazó, durva- finom szabályozással készített transzformátor – az előbb említett előnyöktől eltekintve – a gazdaságosabb.

 

 

Várható impakt, további kutatás                 

A bemutatott algoritmusok ipari környezetben történő hasznosítása azok fejlesztésétől kezdődően folyamatos. A metaheurisztikus optimalizáló kódomat a High Voltage Solutions kft.-nél, illetve ipari partnereinél alkalmazzák.

Az ásványiolaj-alapú transzformátorolajok rendkívül környezetszennyezőek, ezért napjainkban egyre jobban előtérbe kerülnek a természetes, észter- és szilikonalapú olajok. Ezeknek az anyagoknak a viszkozitása, termikus és öregedési tulajdonságai azonban különböznek az ásványi olajokétól. A metaheurisztikus optimalizáló módszer fejlesztésével ezeknek az olajoknak a gazdaságossága, illetve a transzformátorok főméreteire gyakorolt hatása is vizsgálhatóvá válik.

 

Saját publikációk, hivatkozások, linkgyűjtemény

                                           

(J1) T. Orosz ,A., Sleisz and Z. A., Tamus. "Metaheuristic optimization preliminary design process of core-form autotransformers," IEEE Transaction on Magnetics, vol. 52 no. 4, April, 2016 (IF: 1.28)

(J2) T. Orosz, B. Borbély, Z. Á. Tamus,", Performance Comparison of Multi Design Method and Meta-Heuristic Methods for Optimal Preliminary Design of Core-Form Power Transformers," Periodica Polytechnica Electrical Engineering and Computer Science, vol 61, no. 1, 2017

(J3) T. Orosz and Z. Á. Tamus. "Impact of the Cooling Equipment on the Key Design Parameters of a Core-Form Power Transformer." Journal of Electrical Engineering, vol. 67 no. 6, pp. 399–406, 2016. (IF: 0.498)

(J4) T. Orosz, P. M. Sőrés, D. Raisz, Z. Á. Tamus, "Analysis of the Green Power Transition on Optimal Power

Transformer Design," Periodica Polytechnica Electrical Engineering and Computer Science, vol. 59 no. 3, pp. 125-131., 2015.

(J5) T. Orosz, G. Kleizer, T. Iváncsy, Z. Á. Tamus, "Comparison of Methods for Calculation of Core-Form Power Transformer’s Core Temperature Rise," Periodica Polytechnica Electrical Engineering and Computer Science, vol. 60, no. 2, pp. 88-95., 2016.

(J6) T. Orosz, T. Nagy, Z. A. Tamus, "A Generalized Geometric Programming Sub-problem of Transformer Design Optimization", "Technical Innovation of Smart Systems", Springer, pp. 373-381, 2017

(J7) T. Orosz and Z. Á. Tamus, "Impact of the Short Circuit Impedance and the Tap Changing Method Selection on the Key-design Parameters of Core-form Power Transformers." Springer, Electrical Engineering [minor revision] (IF: 0.662)

(C1) T. Orosz, Á. Sleisz, I. Vajda, "Core-Form Transformer Design Optimization with Branch and Bound Search and Geometric Programming", in 2014 55^th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Lettország, 2014.

(C2) P. Sorés, T. Orosz, I. Vajda, "Lifetime Cost Sensitivity Assessment in Optimal Core-form Power Transformer Design", in: 9th International Conference on Deregulated Electrical Market Issues in South Eastern Europe, Nicosia, Cyprus, 2014.

(C3) T. Orosz, I. Vajda, "Power Transformer Design Optimization with Geometric Programming," in Topical Problems in the Field of Electrical and Power Engineering: Doctoral School of Energy and Geotechnology II., Parnu, Észtország, 2014.

(C4) T. Orosz, I. Vajda, "Költségoptimális nagytranszformátor tervezés Geometriai Programozás segítségével", in 29. Kandó Konferencia = 29th Kandó Conference, Budapest, Magyarország, 2013.

 

                                               

Hivatkozások listája:

 

[1] R. M. Del Vecchio, B. Poulin, P. T. Feghali, D. M. Shah, and R. Ahuja, Transformer design principles: with applications to core-form power transformers. CRC press, 2001.

[2] H. M. Ryan, High voltage engineering and testing 3rd Edition. No. 32, IET, 2013.

[3] P. Abetti, W. Cuthbertson, and S. Williams, „Philosophy of applying digital computers to the design of electric apparatus,” American Institute of Electrical Engineers, Part I: Communication and Electronics, Transactions of the, vol. 77, no. 3, pp. 367–379, 1958.

[4] Kiss L., Karsai K., Kerényi D., Nagytranszformátorok, Műszaki Könyvkiadó, 1973.

[5] G. Kapp, Transformatoren für Wechselstrom und Drehstrom [Transformers for Single and Multiphase Currents: A Treatise on Their Theory, Construction, and Use]. Charleston SC, United States: Nabu Press, 2012 [1900]. Originally published in: 1900.

[6] G. Ujházy, Eroátviteli transzformátorok gépi számításának kérdései [Application of Computers for Power Transformer Design]. PhD thesis, Budapest University of Technology and Economics, 1969. [In Hungarian].

[7] E. I. Amoiralis, M. A. Tsili, and A. G. Kladas, „Transformer design and optimization: a literature survey,” Power Delivery, IEEE Transactions on, vol. 24, no. 4, pp. 1999–2024, 2009.

[8] P. S. Georgilakis, Spotlight on modern transformer design. Springer Science & Business Media, 2009.

[9] S. Corhodzic and A. Kalam, „Assessment of distribution transformers using loss capitalization formulae,” Journal of Electrical and Electronics Engineering Australia, vol. 20, no. 1, pp. 43–48, 2000.

[10] „IEEE loss evaluation guide for power transformers and reactors,” 1992.

[11] S. Boyd and L. Vandenberghe, Convex optimization. Cambridge university press, 2004.

[12] R. A. Jabr, „Application of geometric programming to transformer design,” Magnetics, IEEE Transactions on, vol. 41, no. 11, pp. 4261–4269, 2005.

[13] A. White, „Tapchanging-the transformer designer’s perspective,” in Developments On-Load Tapchangers: Current Experience and Future, IEE European Seminar on, pp. 4–1, IET, 1995.

[14] O. W. Andersen, „Transformer leakage flux program based on the finite element method,” IEEE Transactions on Power Apparatus and Systems, vol. PAS-92, pp. 682–689, March 1973.