Csonka Pál Doktori Iskola 

BME Építészmérnöki Kar, Szilárdságtani és tartószerkezeti Tanszék

Témavezető: Dr. Sipos András Árpád

Vékony filmek ráncos mintázatai

A kutatási téma néhány soros bemutatása

A vékony filmekre jellemző ráncosodás, mint kihajlási jelenség, illetve a ráncok alakjának vizsgálata számos gyakorlati probléma során kulcsfontosságú. Napvitorlák tervezésénél, légzsákok, membrán szerkezetek és görgős gyártósoron vezetett filmek esetén a ráncosodás elkerülése vagy csökkentése elsődleges szempont.

1. ábra. Sátorszerkezet modelljének ráncosodása tönkremeneteli helyzetben

 

A ráncosodás leírására alkalmazott modellek máig élénk vita tárgyát képezik a kutatók között, aminek egyik oka a téma újszerűsége és a viszonylag kevés rendelkezésre álló kísérleti eredmény. Jelen kutatás célja a jelenség modellezésére széles körben alkalmazott Kármán-féle lemezelmélet és annak nagy nyúlásokra kiterjesztett változatának segítségével különféle ráncosodási problémák vizsgálata, a számítások összevetése kísérleti eredményekkel és az elméletek alkalmazhatósági határainak pontosabb feltérképezése.

 

A kutatóhely rövid bemutatása

A Szilárdságtani és Tartószerkezeti Tanszék változatos profilját elméleti, kísérleti és tartószerkezeti kutatások határozzák meg. A különböző anyagú tartószerkezetek tervezésének és méretezésének kérdésein túl oktatóink foglalkoznak többek között elemekből épített oszlopok és ívek modellezésével, vékony héjak és filmek stabilitásvesztésével, emlékező fémekkel, kavicsok alakfejlődésével és ütközéseknek kitett merev testek stabilitásával.

 

A kutatás történetének, tágabb kontextusának bemutatása

A ráncosodás vékony, néhány századmilliméter vastagságú lemezeken, azaz filmeken nyomófeszültség hatására jelentkező stabilitásvesztés. A vékony filmek gazdag morfológiával rendelkeznek, a ráncosodáson kívül beszélhetünk még gyűrődésről, élképződésről és hólyagosodásról, amely jelenségeket összefoglalóan mintázatképződésnek nevezzük. Noha a nyomással terhelt vékony lemezek kihajlásával már Timoshenko az 1936-os könyvében is foglalkozott, a vékony filmeken kialakuló ráncosodás Cerda, Ravi-Chandar és Mahadevan 2002-es Nature-ben megjelent publikációja után vált kedvelt kutatási területté. Munkájukban két végén befogott, húzott téglalap alakú filmekkel foglalkoztak, amelyek esetén az ún. Poisson hatás miatt nem csak húzó, hanem nyomófeszültségek is ébrednek a filmben, ami ráncosodáshoz vezethet.

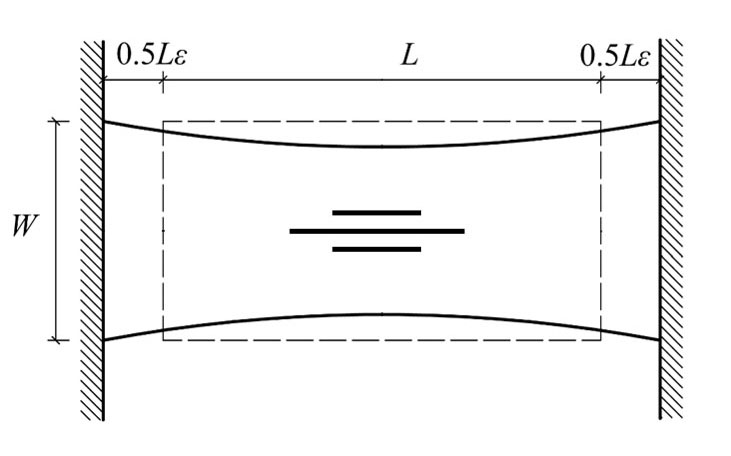
2. ábra. Két végén befogott, húzott film ráncosodása

 

A viselkedés leírására az egyik legelterjedtebb modell a Kármán-féle nagy lehajlású vékony lemezek elmélete, amelyet azonban gyakran olyan jelenségek leírására is alkalmaztak, melyek az elmélet alapfeltételezéseivel nincsenek összhangban. Healey 2013-as publikációjában az eredeti, kis nyúlásokat feltételező modellt kiterjesztette nagy nyúlásokra és a húzott téglalapokon egy kritikus megnyúlási érték felett a ráncok eltűnését jósolta. Megfogalmazta továbbá, hogy a ráncosodás csak bizonyos oldalarányú téglalapok esetén jelentkezik.

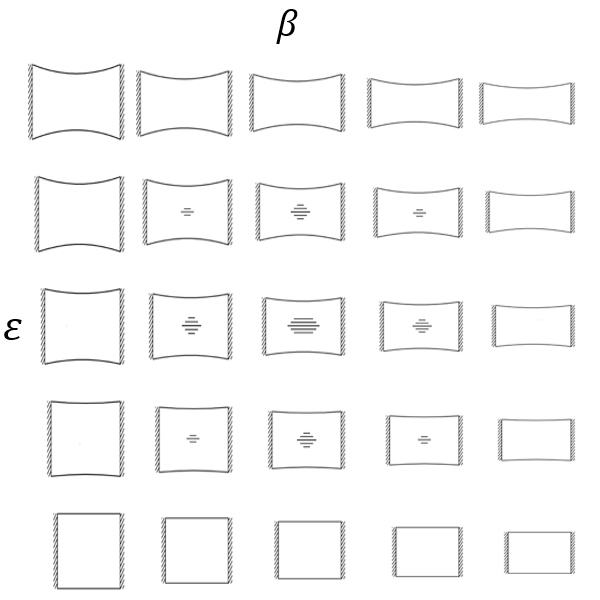
3. ábra.  A nagy nyúlásos elmélet előrejelzése (: oldalarány, : megnyúlás)

 

Az irodalomban addig rendelkezésre álló kis számú kísérleti eredmény azonban nem volt alkalmas az előrejelzések igazolására. A kísérletek kivitelezésének egyik legkritikusabb része az elegendően vékony és kellően rugalmas anyag kiválasztása. A szükséges vastagságban elérhető rugalmas anyagok főként a polimerek közül kerülnek ki, amelyek anyagtulajdonságai azonban jelentősen befolyásolják a ráncosodást, ezzel nehezítve a mérési és számítási eredmények összevetését.

 

A kutatás célja, a megválaszolandó kérdések.

A kutatás egyik célja két végén befogott, húzott filmek ráncosodásának átfogó kísérleti vizsgálata valamilyen, az irodalomban hivatkozott kísérleti anyagoknál sokkal rugalmasabb film segítségével. A kísérletek során különböző oldalarányú téglalapok szisztematikus vizsgálata szükséges a nagy nyúlásos elmélet előrejelzéseinek igazolásához. A kísérletek rámutathatnak a nagy nyúlásokra való kiterjesztés szükségességére. Mivel a Kármán-féle elmélet alapvetően rugalmas, izotróp, homogén anyagmodellt feltételez, további fontos feladat a választott film anyagtulajdonságainak feltérképezése, és azok ráncosodást befolyásoló hatásának vizsgálata.

 

A kísérletek során megfigyeltük, hogy ciklikus terhelés esetén bizonyos oldalarányú téglalapok az első megnyújtás során ráncosodásmentesek maradnak, a leterheléskor és a további megnyújtások alatt azonban ráncosodnak. A kutatás egyik részében erre a viselkedésre kerestünk magyarázatot.

 

A kísérleti eredmények számításokkal való összevetéséhez egy numerikus algoritmusra van szükség, amely mind a Kármán-féle, mind pedig a nagy nyúlásos elmélet számítására alkalmas. A Kármán-féle lemezelmélet egyenletei nemlineáris, negyedrendű parciális differenciálegyenlet rendszert alkotnak, amelynek megoldására olyan a végeselem módszeren alapuló útkövető eljárás fejlesztését tűztük ki célul, amely lehetővé teszi bonyolultabb anyagmodellek implementációját, illetve téglalaptól eltérő geometriájú filmek ráncosodásának modellezését.

 

A valós problémák során azonban a ráncosodás nem korlátozódik síkbeli felületekre, ezért szükséges a modell kiterjesztése három dimenzióba beágyazott, térben görbült felületekre is. Az irodalomban fellelhető modellek általában a felület paraméterezésének ismeretét feltételezik, és a Kármán-féle elmélet Airy feszültségfüggvénnyel felírt alakjából indulnak ki. Mivel a nagy nyúlásos elmélet esetén nem létezik ilyen feszültségfüggvény, ezért a kutatás következő célja egy mindkét elméletre és általános geometriára alkalmazható modell implementációja volt. Megválaszolandó kérdés, hogy a felület görbülete és a nagy nyúlásos kiterjesztés hogyan befolyásolja a ráncosodást.

 

Módszerek

A kísérletek során elsőként polietilén filmeket vizsgáltunk, amelyekkel kvalitatív módon igazoltuk a nagy nyúlásos elmélet ráncok eltűnésére vonatkozó előrejelzését [3]. Majd különböző szélességű, 50 mm hosszúságú, 20 mikron vastagságú poliuretán filmeket elmozdulásvezérelt módon terheltünk és szemrevételezéssel kerestük az adott oldalarány esetén a ráncok eltűnéséhez szükséges megnyúlást [2].

 

 

4. ábra. Kísérleti eredmények különböző oldalarányok és megnyúlások esetén

 

Ezután a tanszék Czakó Adolf laboratóriumában lévő törőgép segítségével meghatároztuk a film feszültség-megnyúlás diagramját hossz-, haránt- és 45°-os irányban. A mérés segítségével megállapítottuk, hogy az előfeszített filmek közel lineárisan rugalmasan viselkednek így a Kármán-féle elmélettel jól modellezhetőek, azonban az előfeszítés jelentős ortotrópiát okoz. Az anyagtulajdonságok hatásának figyelembevételéhez ezért a modellbe elsőként az ortotróp anyagmodellt implementáltuk.

 

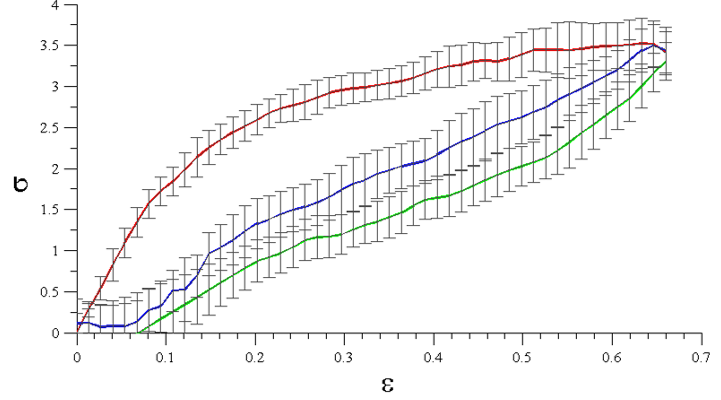
5. ábra.  Az alkalmazott film feszültség-megnyúlás diagramja hosszirányban (piros: felterhelés, zöld: leterhelés, kék: újraterhelés)

 

A teljes jelenség vizsgálatához és a ciklikus terhelés során megfigyelt viselkedés magyarázatához azonban az irodalommal összhangban a poliuretán filmek modellezésére általánosan alkalmazott Mooney-Rivlin hiperelasztikus anyagmodell és valamilyen károsodási modell beépítésére volt szükség. Az ún. Mullins-hatás jól magyarázta a viselkedést, lényege, hogy a felterhelési ágon nem feltételez károsodást, a leterhelési ágakon pedig az addig elért maximális megnyúlástól függő mezőkkel veszi figyelembe a károsodást.

 

6. ábra.  Ciklikusan terhelt poliuretán film ráncosodása

 

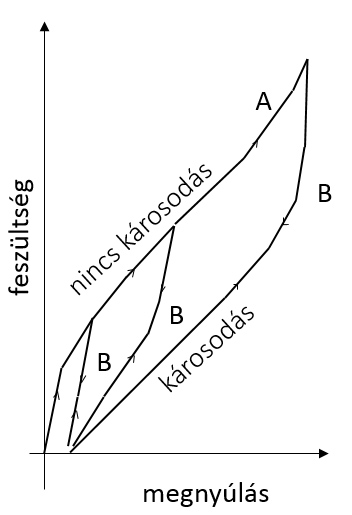
7. ábra.  A Mullins-hatás lényege (A: felterhelési ág, B: leterhelési ágak)

 

A Kármán-féle és a nagy nyúlásos elmélet implementációjához először Matlabban a C1 folytonos, téglalap alakú végeselemeket alkalmazó algoritmust implementáltunk. A kód alkalmas volt a két végén befogott, húzott filmek vizsgálatára, azonban mivel egyéb anyagmodellek és geometriák implementációja során nehézségekbe ütköztünk, ezért egy általánosabb végeselemes könyvtár használata mellett döntöttünk. A FEniCS nyílt forráskódú végeselemes könyvtárra épülő útkövető eljárást fejlesztettünk C++ nyelven. A FEniCS előnye, hogy az egyenleteket és a geometriát egymástól elkülönítve kezeli, így a segítségével létrehozott programban a téglalaptól eltérő geometriák és új anyagtörvények könnyen implementálhatóak. A programmal az egyenletek gyenge alakját oldjuk meg az ún. Discontinuous Galerkin módszerrel, ami az elemperemeken a deriváltak folytonosságát gyengén kényszeríti, és ezáltal lehetővé teszi, hogy negyedrendű egyenletek esetén is csak C0 folytonos elemeket alkalmazzunk. Az útkövető eljárással az egyenletrendszer Jacobi-mátrixának legkisebb abszolút értékű sajátértékének előjelét számítottuk, és segítségével detektáltuk a ráncok megjelenéséhez, illetve eltűnéséhez tartozó bifurkációs pontokat.

 

8. ábra.  Axiálisan nyomott, csuklósan megtámasztott henger kihajlási alakja

 

A Kármán-féle elmélet háromdimenziós felületekre való kiterjesztésére az irodalomban számos modell fellelhető. Ezek azonban általában valamilyen speciális geometriára korlátozódnak, illetve az egyenletek olyan egyszerűbb alakjából indulnak ki, amely az Airy feszültségfüggvénnyel felírható. Belátható, hogy a nagy nyúlásos elmélet esetén nem létezik feszültségfüggvény. A FEniCS másik előnye, hogy három dimenzióba ágyazott felületek esetén a deriváltakat automatikusan az érintősíkban értelmezi, emiatt a modell könnyen kiterjeszthető görbült felületekre. A görbült felületekre felírt modellben azonban a nyúlási energia számításánál a felület görbületét figyelembe kell venni. A görbület a felületi normális segítségével számítható, amely vagy ismert, vagy pedig a végeselemek csomópontjaiból approximálható.

 

Eddigi eredmények

Az ortotrópia figyelembevételével az előfeszített poliuretán filmeken kvantitatív egyezést kaptunk a kísérleti eredmények és a nagy nyúlásos elmélettel végzett számítások között. Ezzel sikerült igazolni a nagy nyúlásos kiterjesztés szükségességét. Kísérleteinkkel megmutattuk, hogy a ráncosodás valóban csak bizonyos oldalarányú téglalapok esetén jelentkezik.

 

Numerikus úton vizsgáltuk az ortotrópia hatását a ráncos konfigurációkat (oldalarány-megnyúlás) tartalmazó tartomány kiterjedésére. Megállapítottuk, hogy minél nagyobb az ortotrópia, adott vastagság esetén annál nagyobb ez a tartomány. Az irodalomban korábban végzett kísérletek során az alkalmazott polimereket izotrópnak tekintették, ezért fontos eredmény, hogy az ortotrópia befolyásolja a ráncosodást.

 

A 8. ábra pontvonallal jelölt görbéje a nyomófeszültségek határát jelenti: a vonalon kívül eső területen vastagságtól függetlenül nem jelentkezik nyomófeszültség a filmben. Belátható, hogy a görbe nem a végtelenbe tart, azaz bármilyen kis vastagság esetén létezik kritikus megnyúlási érték, amely felett már nem ráncosodik a film.

 

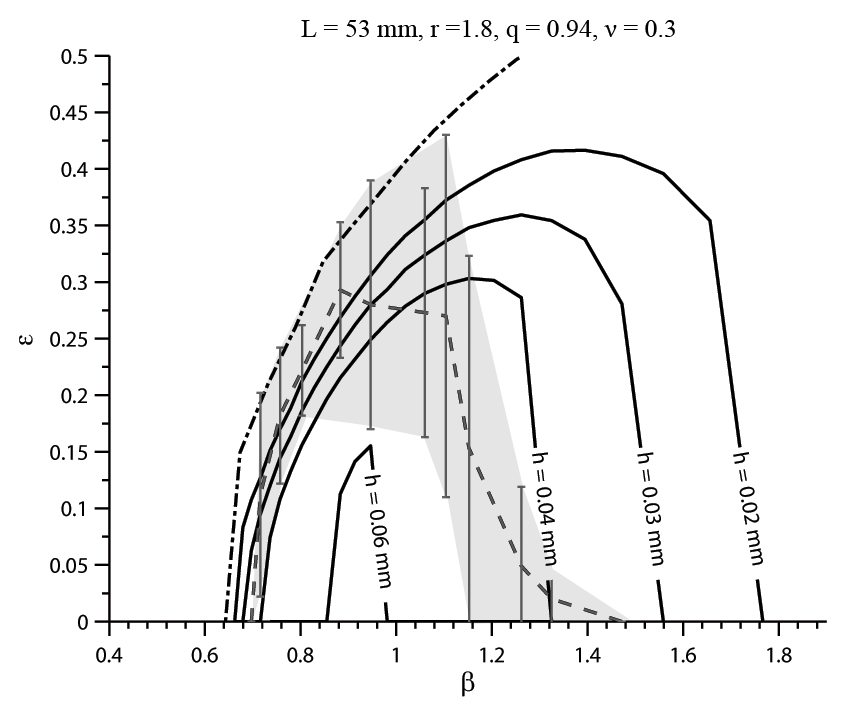
9. ábra. Előfeszített poliuretán filmeken adott oldalarány esetén a ráncok eltűnéséhez tartozó kritikus megnyúlások összevetése számítási eredményekkel (r,q: ortotrópia paraméterek, : Poisson tényező, h: vastagság)

 

A Mullins-hatás figyelembevételével a teljes ciklikus folyamatra jó egyezést kaptunk a számítási és a kísérleti eredmények között. Megállapítható, hogy az előfeszítés során a polimer szerkezetének károsodása miatt megváltoznak az anyagtulajdonságai, ami miatt következő ciklusokban már ráncosodik. Ha azonban a maximális megnyúlást nem növeljük tovább, úgy nem történik további károsodás, és az anyag közel lineárisan rugalmasan viselkedik.

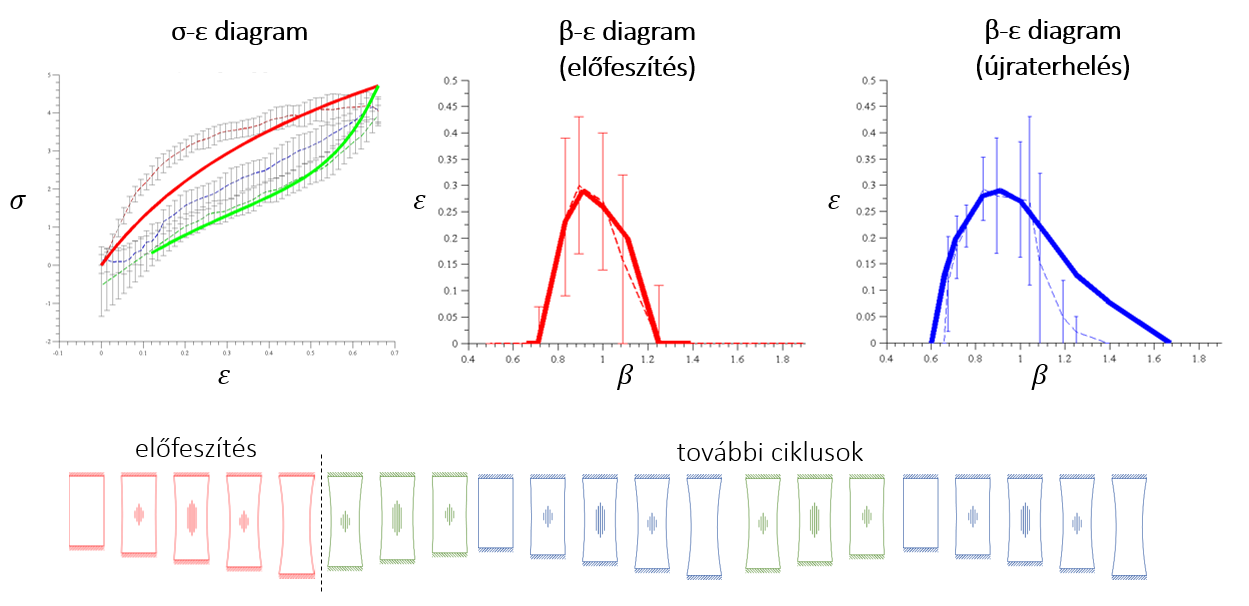
10. ábra. A teljes ciklikus terhelés modellezése a Mullins-hatás figyelembevételével

 

A görbült felületekre kiterjesztett modell validációjához axiálisan terhelt, csuklósan megtámasztott hengerfelületek kihajlásához tartozó kritikus feszültségeket számítottuk, majd az irodalomban fellelhető analitikus eredményekkel vetettük össze. A görbület hatásának vizsgálatához két végén befogott, húzott hengerfelületek ráncosodását vizsgáltuk. Megállapítható, hogy a görbület növelésével adott megnyúlás esetén megszüntethető a ráncosodás, és létezik kritikus görbület, amely felett nem jelentkeznek ráncok.

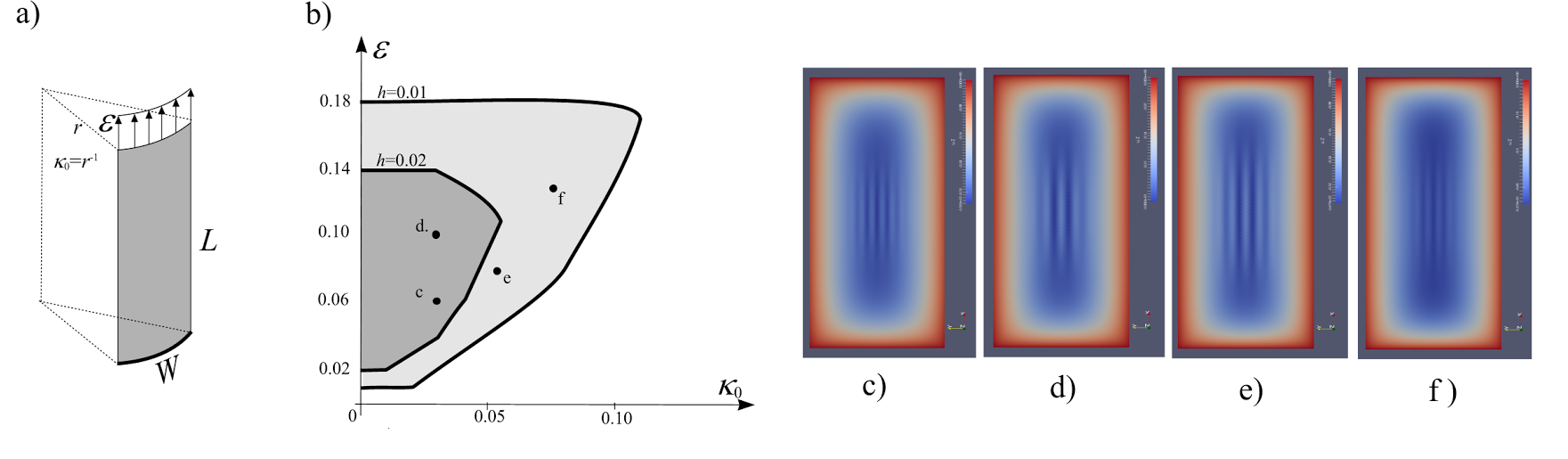
11. ábra. A kezdeti görbület hatása a ráncosodásra

 

Ezután axiális és hidrosztatikus teherrel egyaránt terhelt hengerfelületek ráncosodásánál vizsgáltuk a két elmélet közötti különbséget. Belső nyomással terhelt hengerek nem ráncosodnak (p<0), a külső nyomással terhelt hengerek (p>0) azonban húzás hatására ráncossá válnak. A téglalaphoz hasonlóan azonban itt is létezik kritikus megnyúlási érték, amely felett újból ráncosodásmentes a felület. A Kármán-féle elmélet azonban túlbecsüli a ráncosodáshoz szükséges kritikus megnyúlási értékeket.

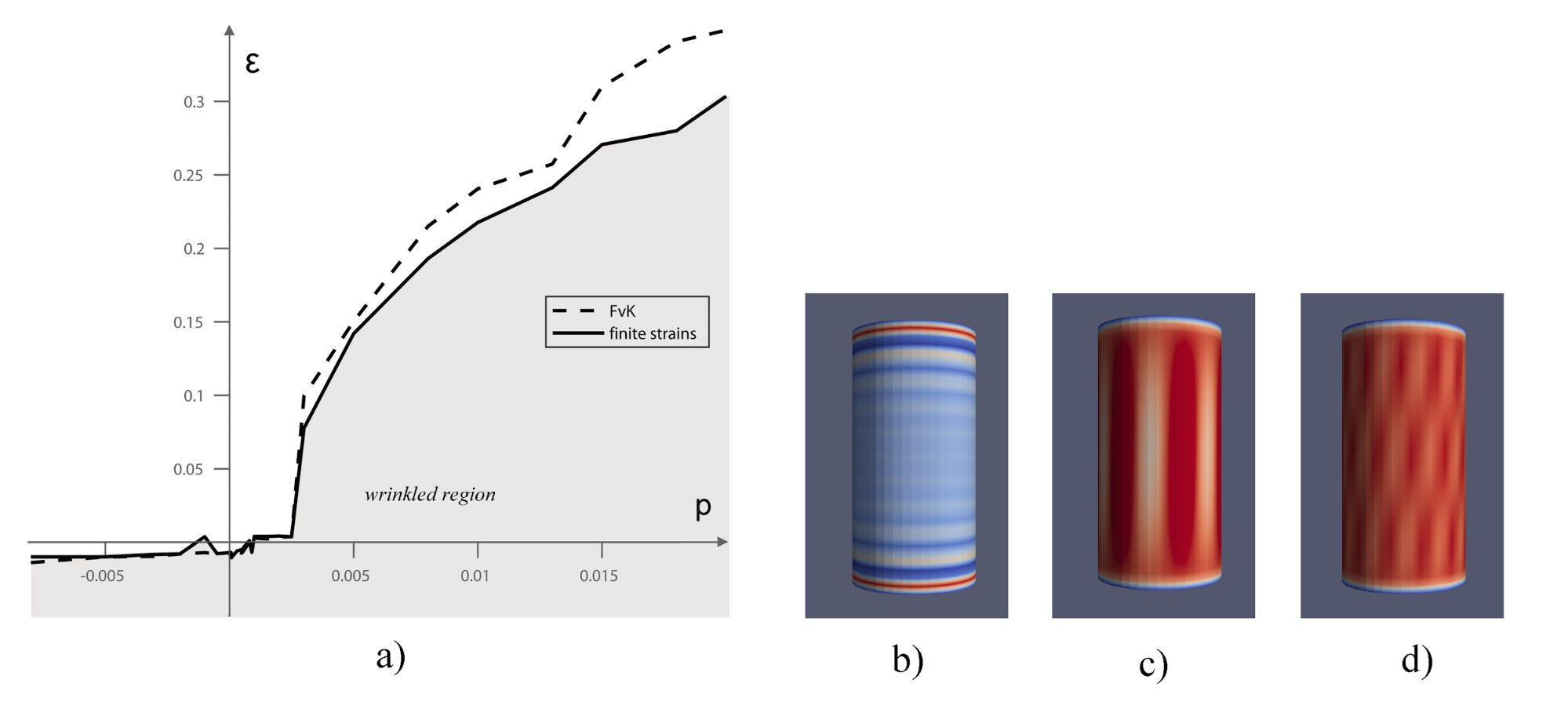
12. ábra. Axiális és hidrosztatikus teherrel együttesen terhelt két végén megtámasztott, csuklós hengerek ráncosodása (folytonos vonal: Kármán-féle elmélet, szaggatott vonal: nagy nyúlásos elmélet)

Várható impakt, további kutatás

A jövőben tervezzük további térbeli problémák vizsgálatát, amelyek esetén a nagy nyúlásos kiterjesztés elengedhetetlen, a kísérletek kivitelezése azonban nehézkes (pl. Möbius-szalag alakú film ráncosodása). Gyakorlati szempontból érdekes továbbfejlesztési lehetőség a ráncok eltüntetését célzó stratégiák kidolgozása, ami az irodalomban egyre nagyobb hangsúlyt kap. Elméleti szempontból pedig máig nem eldöntött kérdés, hogy a ráncok száma hogyan alakul a húzott téglalapok megnyújtása során. A kapott eredmények hozzájárulnak a ráncosodás modellezésére alkalmas elméletek pontosításához, és rámutatnak a kísérleti eredmények kiértékelése során nem elhanyagolható anyagi tulajdonságok hatásaira.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

[F1] E. Fehér, A. Á. Sipos (2017), Wrinkling patterns of thin films under finite membrane strain, 9th European Nonlinear Dynamics Conference. Budapest, Magyarország, 2017.06.25-30. 1-7. old. ISBN 978-963-12-9168-1

[F2] A. Á. Sipos, E. Fehér (2016), Disappearance of stretch-induced wrinkles of thin sheets: a study of orthotropic films, International Journal of Solids and Structures 97-98: 275-283. old.

[F3] E. Fehér, A. Á. Sipos (2014), Húzott, vékony filmek ráncosodása: a ráncos mintázat keletkezése és eltűnése, Építés-Építészettudomány 42:(1-2) 23-42. old.

[F4] E. Fehér, D. Hegyi, M. Halász, P. Tamás (2011), Wrinkling at the failure of membrane structures, International Symposium on Innovative Technologies and Design. Budapest, Magyarország, 2011.11.21-22. 1-10. old.

 

Szóbeli előadások.

[F5] E. Fehér, A. Á. Sipos (2016), Arclength continuation in FEniCS and its application to the study of wrinkling of ultrathin films, FEniCS’16 Workshop, Oslo, Norvégia, 2016.05.19.

 

Linkgyűjtemény.

http://www.szt.bme.hu/

https://fenicsproject.org

 

Hivatkozások listája.

[R1] Healey, T.J., Li, Q., Cheng, R.B., 2013. Wrinkling behaviour of highly stretched rectangular elastic films via parametric global bifurcation. J. Nonlinear Sci.23:777–805

[R2] Logg A., Mardal K-A., Wells G. N. Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book, Springer-Verlag Berlin Heidelberg, 84, 2012.

[R3] Timoshenko S.P., Gere J. M., 1961. Theory of elastic stability. McGraw-Hill Book Company, Inc., New York.

[R4] Karman T., Tsien H. S., 1941. The buckling of thin cylinders under axial compression and bending. Journ. Aero. Sci.8, No. 8 p. 303.

[R5] Cerda E., Mahadevan L., 2003. Geometry and physics of wrinkling. Phys. Rev. Lett. 90, 1-4.

[R6] Cerda E., Ravi-Chandar K., Mahadevan L., 2002. Wrinkling of an elastic sheet under tension. Nature 419, 579-580.

[R7] Davidovitch B., Schroll R.D., Vella D., Add-Bedia M., Cerda E., 2011. Prototypical model for tensional wrinkling in thin sheets. PNAS 108 (45), 18227-18232.

[R8] Friedl N., Rammerstorfer F., Fischer F., 2000. Buckling of stretched strips. Comput. Struct. 78, 185-190.

[R9] Donnell L.H., 1933. Stability of thin-walled tubes under torsion. NACA Rep. 479.

[R10] Rivière B., 2008. Discontinuous Galerkin Methods for Solving Elliptic and Parabolic Equations: Theory and Implementation. SIAM Frontiers in Applied Mathematics