Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola   

BME GPK, Gyártástudomány és -technológia Tanszék

Témavezető: Dr. Szalay Tibor

A fajlagos forgácsolóerő tapasztalati modelljének kiterjesztése a vékonyforgács-képződés tartományára

A kutatási téma néhány soros bemutatása

Doktori kutatómunkám témája a forgácsolhatóság vizsgálata és leírása a mechanikus forgácsolás energetikai paramétereinek segítségével, hagyományos és nagy szilárdságú szerkezeti anyagok precíziós és mikroforgácsolására vonatkozóan.

A kutatóhely rövid bemutatása

Doktori kutatásaimat a BME Gyártástudomány és –technológia Tanszéken végeztem Dr. Szalay Tibor témavezetésével. Tanszékünk nagy hangsúlyt fektet a hagyományos és korszerű gyártási ismeretek átadására, a korszerű technológiák elméleti alapjainak lefektetésére, kidolgozására. Ennek öröksége számos korábbi és aktuálisan is futó hazai (OTKA), valamint nemzetközi (EU támogatású közös és TéT) együttműködési projektben, illetve ipari kutatási megbízásokban realizálódik.

A kutatás történetének, tágabb kontextusának bemutatása

A mechanikus forgácsolás folyamatának tudományos kutatása és leírása, azaz a forgácsoláselmélet több mint egy évszázados múltra tekint vissza [1]. Ennek egyik fő témaköre a forgácsolhatóság vizsgálata, vagyis annak leírása, hogy mi módon lehetséges / célszerű az egyes alapanyagokat forgácsolni adott technológiai feltételek mellett [2, B1].

A forgácsleválás a munkadarab anyagában kialakuló kontrollált repedésterjedés és a forgács képlékeny alakításának eredménye. Ebben a megközelítésben a forgácsolhatóság az alapanyag mechanikai viselkedését jellemzi. Az anyagszerkezet, összetétel és a technológiai beállítások együttesen befolyásolják a folyamat energetikai körülményeit, így a forgácsolási erők és energia (teljesítmény) értékét. A forgácsolási erők tudományos értelmezésének és kutatásának két jelentős mérföldköve:

• Ernst és Merchant (1941) nyírási sík definiálásán alapuló erőmodellje [3];

• Kienzle és Victor (1957) tapasztalati erőmodellje a fajlagos forgácsolóerő fogalmának bevezetésével [4].

Leginkább a Kienzle-Victor modell fedezhető fel a gyakorlatban, köszönhetően az egyszerű, gyors és általános alkalmazhatóságnak. Emellett ez sikeresen kezeli a mérethatás jelenségét is, vagyis azt, hogy a forgácsolási erők nemlineárisan változnak a forgács keresztmetszeti jellemzőivel.

Az ipari alkatrészgyártásban egyre nagyobb hangsúly helyeződik a precíziós és mikromegmunkálásokra, ahol a forgácsvastagság mikrométer nagyságrendben mozoghat. Ez általános szerkezeti anyagoknál (pl. acéloknál) már a szemcseméret nagyságrendje, így a mérethatás itt fokozottan érvényes [5]. Ennek modellszintű leírása elengedhetetlenül szükséges a technológiai lehetőségek és korlátok célzott azonosításához.

A kutatás célja, a megválaszolandó kérdések

A forgácsképződés 3 fő anyagalakítási folyamatra bontható:

1. Repedésterjedés: a munkadarab anyagában létrejött mechanikai feszültség eléri a törési feszültséget, ezáltal létrejöhet a forgács (1/c. ábra).

2. Képlékeny alakítás: egyrészt a forgácstő és a szerszám homlokfelületén legördülő forgács, másrészt a megmunkált felület szenved maradó alakváltozást (1/a. és 1/b. ábrák).

3. Rugalmas alakváltozás: a szerszámél nyomó hatásának köszönhetően rugalmasan alakváltozik a megmunkált felület, mely visszarugózása során felsúrlódik a szerszám hátfelületére (1/a. ábra).

A megmunkált felület rugalmas és képlékeny deformációját vasalóhatásnak nevezzük, és ez önmagában nem eredményez forgácsképződést. Az elméleti forgácsvastagság (h) lecsökkenthető olyan kritikus értékig, melynél már a vasalóhatás lép fel dominánsan, ezáltal destabilizálva a forgácsképzést. Ez a minimális forgácsvastagság (h_m), mely a beállítható előtolás alsó korlátjaként értelmezhető [6].

 

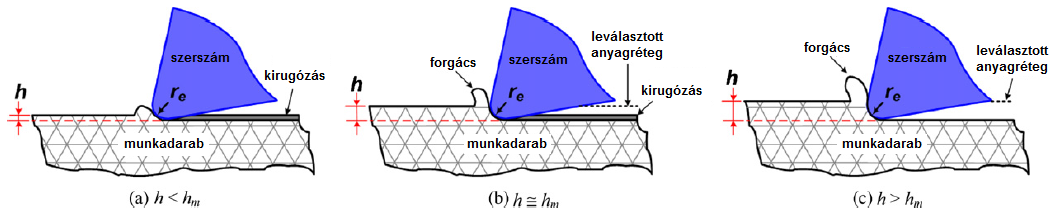
1. ábra: Alakítási folyamatok és a minimális forgácsvastagság kapcsolata [6]

 

Az új termékeken egyre inkább megfigyelhető a miniatürizálás, azaz a névleges geometriai méretek csökkenése és a tűréstartományok szigorítása [7]. Ez szükségszerűen okozza a technológiai paraméterek, így a forgácsvastagság miniatürizálását is.
Kérdés tehát: milyen egyszerű, az ipari gyakorlatban is hatékonyan alkalmazható modellel lehetne jellemezni az anyagok forgácsolhatóságát oly módon, hogy:

1. a modell érvényes legyen a technológiai paraméterek szélsőséges tartományain;

2. információt nyerjünk a forgácsképződés során végbemenő alakítási folyamatok minőségéről;

3. meghatározhatók legyenek a precíziós és mikromegmunkálások olyan kritikus technológiai korlátjai, mint a minimális forgácsvastagság?

Módszerek

A modellezési módszer meghatározása

A fajlagos forgácsolóerő görbéje szemléletes válaszként szolgálhat a megfogalmazott kérdéskörre. A k fajlagos forgácsolóerőnek a h elméleti forgácsvastagság szerinti ábrázolása (továbbiakban: k-görbe, ld. (1) összefüggés) a mérethatásnak is reprezentatív szemléltetője. Lineáris görbék folytonos együtteseként modellezhető a logaritmus rendszerben, ahol az egyes szekciók az anyagalakítás folyamatának különböző minőségére adhatnak utalást (2. ábra). [B2] A szakirodalomban régóta megjelennek ezek a szakaszos modellek [2], melyek azonban:

 

• nem, vagy csak hipotetikusan kötik össze a konvencionális forgács (h > 0,01 mm) és a vékonyforgács (h ≤ 0,01 mm) technológiai sávjait [8];

• csak a vékonyforgács-képződés tartományára vonatkoznak specifikáltan [9].

 

k = F / (h ∙ b) = k1 ∙ h^x + konstans   (1)

 

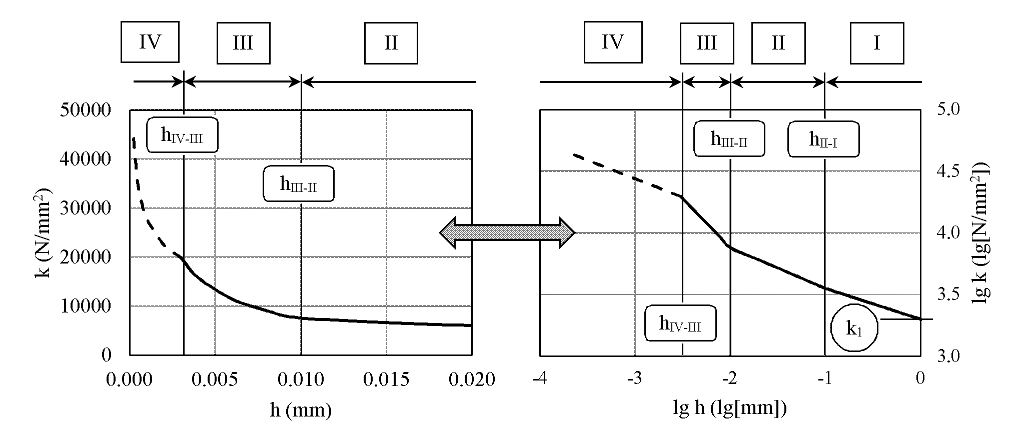
2. ábra: A k-görbe szekciói és töréspontjainak elhelyezkedése [B2]

 

A vizsgálati módszer meghatározása

A k-görbe egyes szekcióinak határai töréspontokkal azonosíthatók, melyek egy-egy névleges forgácsvastagság értékhez rendelhetők (2. ábra). A szekciók jellegének és a töréspontok helyeinek precíz meghatározásához az szükséges, hogy a forgácsvastagság mérési tartományában minél több diszkrét érték jelöltessék meg a mérés bemenő paramétereként. Ezért a homlokmarást választottam vizsgálati módszernek, melynek előnye, hogy:

• általános, az ipari gyakorlatban elterjedt forgácsoló technológia;

• a marás kinematikai viszonyaiból adódóan az elméleti forgácsvastagság értéke zérus és az f_z élenkénti előtolás által korlátozott tartományban mozog (3/b. ábra). E tartomány felbontása a mintavételezési frekvencia által definiálható.

A forgácsolási erők mérését piezoelektromos szenzor segítségével valósítottam meg 3 kötött irányban (X, Y, Z - 3/b. ábra és ld. 4/a. ábra). A marást ütőkéses elven, azaz egyetlen forgácsoló éllel rendelkező szerszámmal (3/a. ábra) végeztem.

 

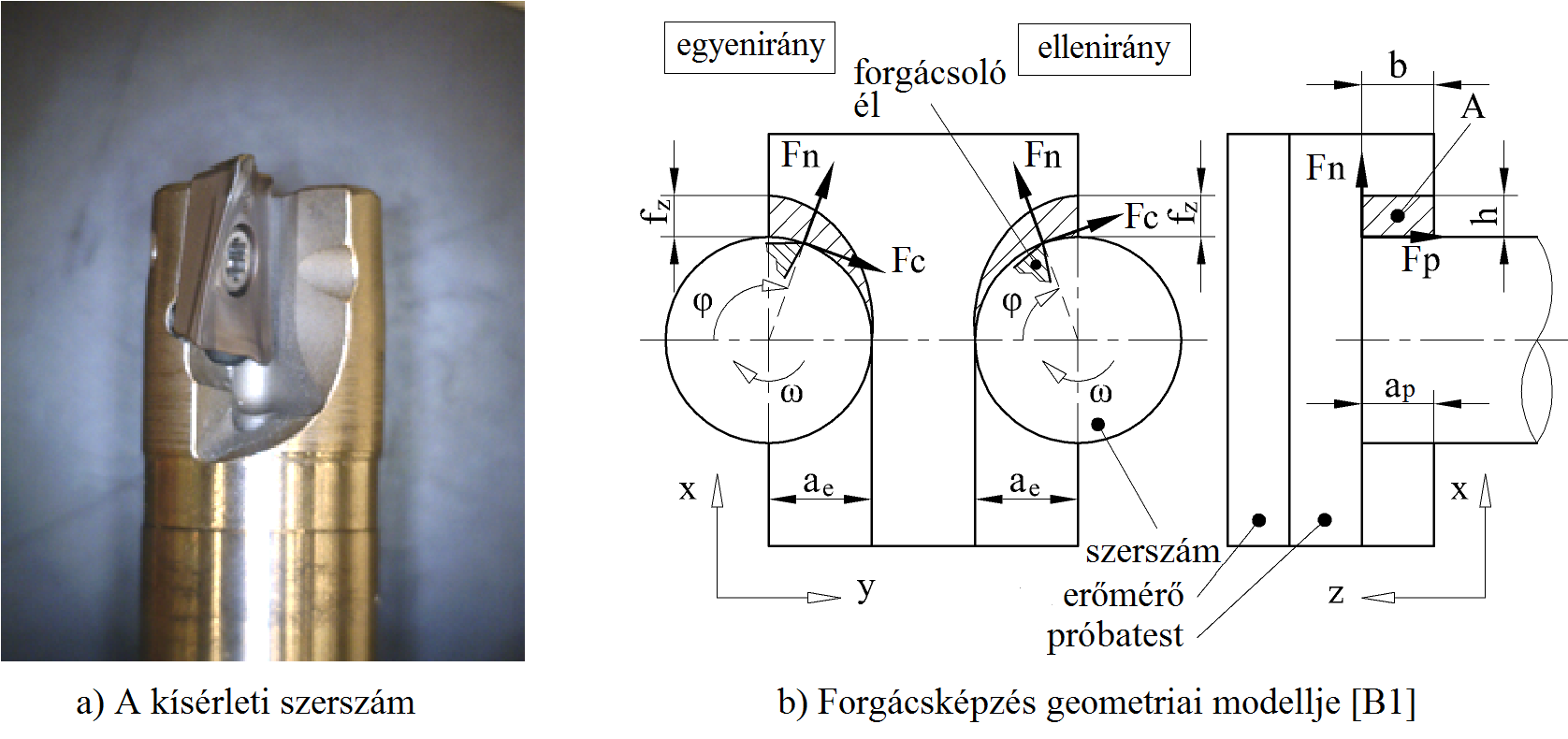
3. ábra: Egyélű homlokmarás geometriai modellje

 

Kísérlettervezés, a kiértékelési módszer meghatározása

Kísérletsorozatom közvetlen célja volt, hogy a k-görbe jellegét, esetleges új szekciójának és töréspontjának létezését igazoljam a vékonyforgács-tartományban. Erre vonatkozóan csak feltételes szakirodalmi információk birtokában voltam [9,10,11,12,13,14,15], így teljes faktoriális kísérlettervet készítettem. A változtatott paraméterek és azok tartományai:

• forgácsoló sebesség: v_c = 50…150 m/min;

• élenkénti előtolás: f_z = 0,01 … 0,16 mm/él/fordulat;

• fogásmélység: a_p = 0,5 … 2 mm;

• marás kinematikai iránya: IR = egyenirány, ellenirány (3/b. ábra).

A próbatestek anyaga: S960QL nagy szilárdságú szerkezeti acél, melyet kiváló anyagszerkezeti homogenitása miatt választottam.

A Kienzle-filozófiát követő modellek meghatározására kész módszertan állt rendelkezésemre, melynek során lineáris regresszióval illesztettem modellfüggvényt a logaritmus tartományba transzformált mérési adatokra (2. ábra és (1) összefüggés alapján). [B4]

A modell megbízhatóságának értékelésére a mért értékekre vonatkoztatott korrigált tapasztalati szórástartományt választottam, ahol a becsült érték (a minta névleges értéke, „átlaga”) a modellből számítandó. A mérési sorozat nagyságát a marószerszám által megtett fordulatok száma határozta meg. A mintavételezést és a számításokat speciálisan e kutatási témához, LabView keretrendszerben fejlesztett programok segítségével végeztem.

 

4. ábra: A mérési környezet

 

Eddigi eredmények

Új töréspont meghatározása a vékonyforgács tartományában

A forgácsolási erőrendszer a mindenkori szerszámélhez rögzített koordináta-rendszerben értelmezendő, mint főerő (F_c), normálerő (F_n) és passzív erő (F_p) (3. ábra). A h elméleti forgácsvastagság és a b elméleti forgácsszélesség pillanatnyi értékei jól becsülhetők a szerszámél névleges pályája alapján. A mért erőkből a fajlagos erőket kiszámítva (ld. (1) összefüggést és 3/b. ábrát), a 4. ábrán látható modell hozható létre. [B3]

 

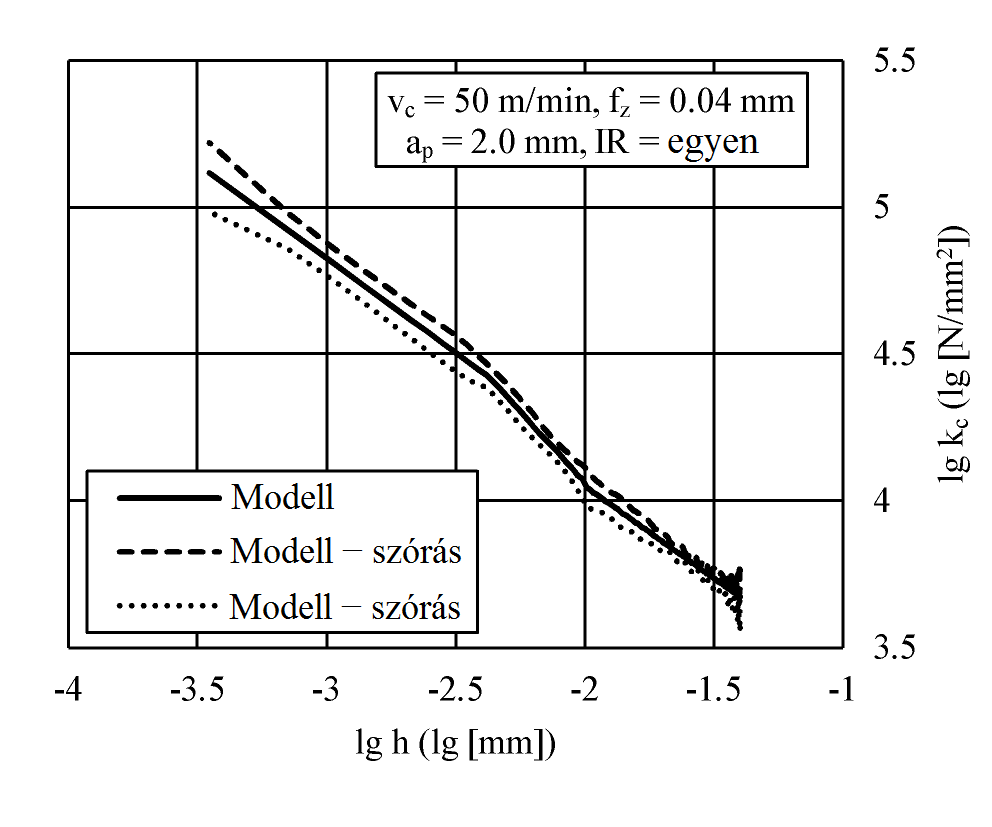
4. ábra: A k-görbe statisztikai modellje egy konkrét mérési adatsorra illesztve [B2]

A szakirodalmi modellekben megjelennek töréspontok a 0,1 mm és 0,01 mm forgácsvastagságoknál, melyek saját méréseim adataiból is kiolvashatók. Megfigyelhető azonban egy új töréspont a h < 0,01 mm tartományban. Ennek névleges helyét az összes mérésre vonatkozóan, a technológiai paraméterek konkrét hatását figyelmen kívül hagyva határoztam meg első lépésben. A 4. és 5/a. ábrákon látható, hogy az új töréspont létezése statisztikai szempontból is alátámasztható. [B2]

 

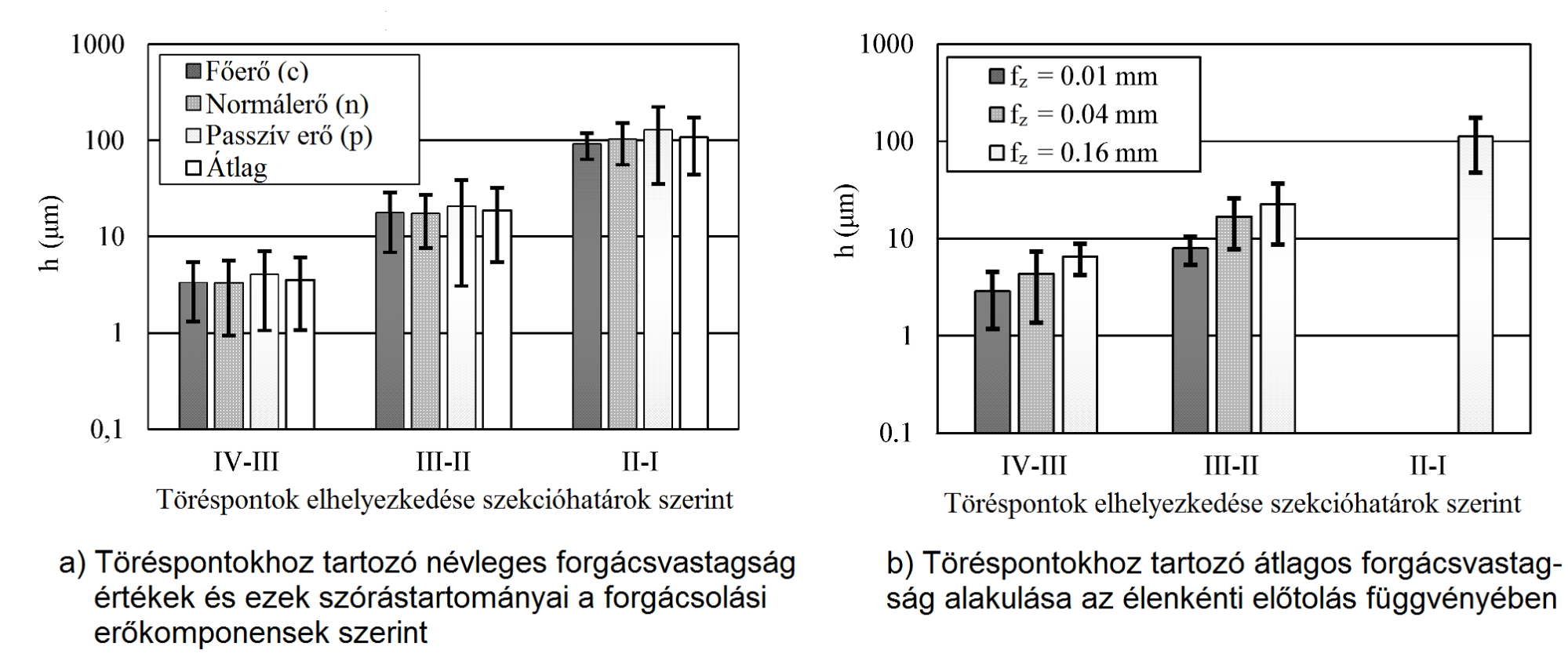
5. ábra: Töréspontokhoz tartozó forgácsvastagság értékek [B2]

 

Töréspontok viselkedése a technológiai paraméterek függvényében

A mérési adatok ANOVA-kiértékelése megmutatta, hogy az f_z élenkénti előtolásnak van szignifikáns hatása a töréspontok helyeire a jelen vizsgálati tartományon. Ez alapján kijelenthető, hogy az előtolás növelésével exponenciálisan nő az adott törésponthoz tartozó forgácsvastagság értéke (5/b. ábra). Ez a jelenség hatványfüggvény-alapú válaszfelület segítségével jól modellezhető statisztikai szempontból is. [B2]

Anyagalakítási folyamatok minősítése és a kritikus forgácsvastagság

Az 1., 2. és 4. ábrák segítségével az alábbi következtetések vonhatók le, illetve hipotézisek állíthatók fel a k-görbe szekcióira vonatkozóan [B2]:

• I. szekció: a makroforgács leválasztásának tartománya, ahol a forgácsolási energia túlnyomó többsége a forgácsképzésben disszipálódik (1/c. ábra);

• II. szekció: a forgácstő képlékeny deformálására fordított forgácsolási energia részaránya megnő, még stabil forgácsképzés történik (átmenet az 1/b. és 1/c. ábrák között);

• III. szekció: a vékonyforgács képződésének tartománya, ahol megnő a vasalóhatás során elnyelt forgácsolási energia részaránya, és feltételesen történik anyagleválás (1/b. ábra);

• IV: szekció: itt a vasalóhatás dominál, anyagleválasztás nem jellemző (1/a. ábra).

A szakirodalomban nem jelenik meg egymástól elkülönítve a III. és IV. szekció, ezáltal a köztük lévő töréspontot sem értelmezett. Mivel a minimális forgácsvastagságot a stabil forgácsképződés alsó határának azonosítására alkalmazzunk [16], bevezetésre javaslom a kritikus elméleti forgácsvastagság fogalmát, mely ténylegesen az anyagleválasztás alsó technológiai korlátját reprezentálja.

Várható impakt, további kutatás

A fajlagos forgácsolóerő görbéjének meghatározásához olyan módszertant és szoftveres háttért dolgoztam ki, mellyel a hagyományos ipari környezetben is hatékony kísérletsorozat végezhető. A k-görbe IV. szekciójának definiálása mutatja, hogy ez a bővített tapasztalati modell kiindulásként szolgálhat az anyagtechnológiai folyamatok részletes feltárásához és leírásához is. Erre vonatkozóan új, különböző technológiájú (homlokbeszúró precíziós esztergálás, mikrofúrás, mikromarás) kísérletek tervezése, végrehajtása és kiértékelése folyamatban van.

A kritikus forgácsvastagság fogalma még hipotetikus. Az e tartományban végzett megmunkálás elsősorban az érintett felület mechanikai tulajdonságait, azon belül a keménységét számottevően befolyásolhatja. E jelenséget precíziós mikrogeometriák felületi kezeléséhez lehetne kihasználni. További kísérleteket tervezek ezen elgondolás vizsgálatára.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája:

 

[B1] Biró I, Czampa M, Szalay T: Experimental Model for the Main Cutting Force in Face Milling of a High Strength Structural Steel, Periodica Polytechnica – Mechanical Engineering, 59(1): 16–22. (2015), DOI: 10.3311/PPme.7516

 

[B2] Biró I, Szalay T: Extension of empirical specific cutting force model for the process of fine chip-removing milling. International Journal of Advanced Manufacturing Technology, Online First edition: 1–9. (2016) – Impakt faktor: 1,568 (2016.06.28.), DOI: 10.1007/s00170-016-8957-x

 

[B3] Biró I, Szalay T, Markos S: Machinability of S960QL high strength structural steel: energetic description of cutting at small chip-thickness in face milling. International Conference on Innovative Technologies (IN-TECH 2013): 237–240. (2013), ISBN: 978-953-6326-88-4

 

[B4] Bíró I, Szalay T: Forgácsolhatóság kísérleti vizsgálata S960QL nagy szilárdságú acélnál. Technika Műszaki Szemle, 55(12): 18–22. (2012)

 

Linkgyűjtemény:

MTMT publikációs lista

 

 

Hivatkozások listája:

 

[1] Szalay T: Modelling in Metal Cutting Theory. Barišić, B. ed. Concurrent Product and Technology Development, 85–102., Kastav: Fintrade and Tours (2009), ISBN: 978-953-96899-9-3

 

[2] Bali J: Forgácsolás. Budapest: Tankönyvkiadó (1985), ISBN: 963-18-0806-8

 

[3] Ernst H, Merchant ME: Chip formation, friction and high quality machined surfaces. Transactions of American Society for Metals, 29: 299–378. (1941)

 

[4] Kienzle O, Victor H: Spezifische Schnittkräfte bei der Metallbearbeitung. Werkstattstechnik und Maschinenbau, 47: 22–25. (1957)

 

[5] Takács M, Verő B: Material Structural Aspects of Micro-Scale Chip Removal. Material Science Forum, 414–415: 377-342. (2003), DOI: 10.4028/www.scientific.net/MSF.414–415.337

 

[6] Aramcharoen A, Mativenga PT, Size effect and tool geometry in micromilling of tool steel. Precision Engineering, 33(4): 402–407. (2009), DOI: 10.1016/j.precisioneng.2008.11.002

 

[7] Wojciechowski S: The estimation of cutting forces and specific force coefficients during finishing ball end milling of inclined surfaces. International Journal of Machine Tools and Manufacture, 89: 110–123. (2015), DOI::10.1016/j.ijmachtools.2014.10.006

 

[8] Altintas Y, Jin X: Mechanics of micro-milling with round edge tools. CIRP Annuals – Manufacturing Technology, 60(1): 77–80. (2011), DOI:10.1016/j.cirp.2011.03.084

 

[9] Campatelli G, Scippa A: Prediction of milling cutting force coefficients for aluminum 6082-T4. Procedia CIRP, 1: 563–568. (2012), DOI: 10.1016/j.procir.2012.04.100

 

[10] Jin X, Altintas Y: Prediction of micro-milling forces with finite element method. Journal of Material Processing Techology, 212(3): 542–552. (2012), DOI: 10.1016/j.jmatprotec.2011.05.020

 

[11] Ko JH, Yun WS, Cho DW, Ehmann KF: Development of a virtual machining system, part 1: approximation of the size effect for cutting force prediction. International Journal of Machine Tools and Manufacturing, 42(15): 1595–1605. (2002), DOI: 10.1016/S0890-6955(02)00137-2

[12] Srinivasa YV, Shunmugam MS: Mechanistic model for prediction of cutting forces in micro end-milling and experimental comparison. International Journal of Machine Tools and Manufacturing, 67: 18–27. (2013), DOI: 10.1016/j.ijmachtools.2012.12.004

 

[13] Balogun VA, Mativenga PT: Impact of un-deformed chip thickness on specific energy in mechanical machining processes. Journal of Cleaner Production, 69: 260–268. (2014), DOI: 10.1016/j.jclepro.2014.01.036

 

[14] Liu K, Melkote SN: Material strengthening mechanisms and their contribution to size effect in micro-cutting. Journal of Manufacturing Science and Engineering, 128(3): 730–738. (2005), DOI: 10.1115/1.2193548

[15] Afazov SM, Ratchev SM, Segal J, Popov AA (2012) Chatter modelling in micro-milling by considering process nonlinearities. International Journal of Machine Tools and Manufacturing, 56: 28–38. (2012), DOI: 10.1016/j.ijmachtools.2011.12.010

 

[16] Ramos AC, Autenrieth H, Strauß T, Deuchert M, Hoffmeister J, Schulze V: Characterization of the transition from ploughing to cutting in micro machining and evaluation of the minimum thickness of cut. Journal of Materials Processing Technology, 212(3): 594–600. (2012), DOI: 10.1016/j.jmatprotec.2011.07.007