|
|
BMe Kutatói pályázat |
|
Fizikai Tudományok Doktori Iskola
BME TTK, Fizika Tanszék/Fizikai Intézet
Témavezető: Dr. Csonka Szabolcs
Elektronok ballisztikus mozgása felfüggesztett grafénban
A kutatási téma néhány soros bemutatása
A grafén az elmúlt évek egyik legintenzívebben és legszélesebb körben kutatott anyaga. Előnyös tulajdonságai közé tartozik átlátszósága, rugalmassága, nagy szakítószilárdsága és elektromos vezetőképessége. Szénatomok hatszöges rácsa alkotja; ilyen, egy atom vastag rétegekből épül fel a grafit.
A legtöbb vezetőben az elektronok gyakran verődnek vissza atomokról, kristályhibákról. Viszont a legnagyobb tisztaságú grafénmintákban az elektronok a minta teljes méretében (tipikusan mikronos, tízmikronos skálán) egyenes mentén haladnak, és csak a grafén pereméről, vagy az elektromos kontaktusokról pattannak vissza, mint a biliárdban, emiatt már nem érvényes a fajlagos ellenállásra vonatkozó Ohm-törvény. Ezt nevezzük ballisztikus transzportnak.
A ballisztikus elektronok hasonlóan viselkednek a fénysugarakhoz: visszaverődhetnek, interferálhatnak egymással, vagyis egy tükrökből, lencsékből, optikai szálakból álló rendszer analógja grafénból is megvalósítható. Ilyen kutatással foglalkozik az elektronoptika területe.
A kutatóhely rövid bemutatása
A mintakészítés a svájci Bázeli Egyetemen, az ottani Nanoelektronika Csoporttal együttműködésben történt, a mérések részben a BME-n születtek. A csoportnak sok tapasztalata van a legjobb minőségű felfüggesztett grafénminták fabrikálásában. A BME Fizika Tanszék kutatói már többször dolgoztak együtt a svájci kollégákkal más kutatási témákban.
A kutatás történetének, tágabb kontextusának bemutatása
A grafén 2004-es felfedezéséig főleg ultratiszta félvezető rétegszerkezetekben, ún. kétdimenziós elektrongázokban (2DEG) vizsgálták az elektronok ballisztikus transzportját. A grafénban azonban a 2DEG-től eltérően széles tartományban hangolható az elektronok sűrűsége, és ezáltal a hullámhossza. Emellett a különleges, lineáris sávszerkezet miatt a grafénbeli, ún. Dirac-elektronok a fényhez, vagy a relativisztikus (közel fénysebességgel mozgó) részecskékhez hasonlíthatók. Relativisztikus jelenségek analógjai is szóba jönnek, például a Klein-alagutazásé: a grafénban az elektronok olyan potenciálgátakon is 100% valószínűséggel képesek áthaladni (merőleges beesésnél), melyek energiája magasabb az elektronénál. Ez klasszikusan olyan, mintha egy labda átjutna egy olyan magas dombon, amire fel se tudna gurulni.
A grafénban ballisztikusan mozgó Dirac-elektronok egyedülálló fizikai jelenségek vizsgálatát teszik lehetővé. Az 1. ábra néhány, a ballisztikus rendszerekben megfigyelhető érdekes jelenséget mutat be.
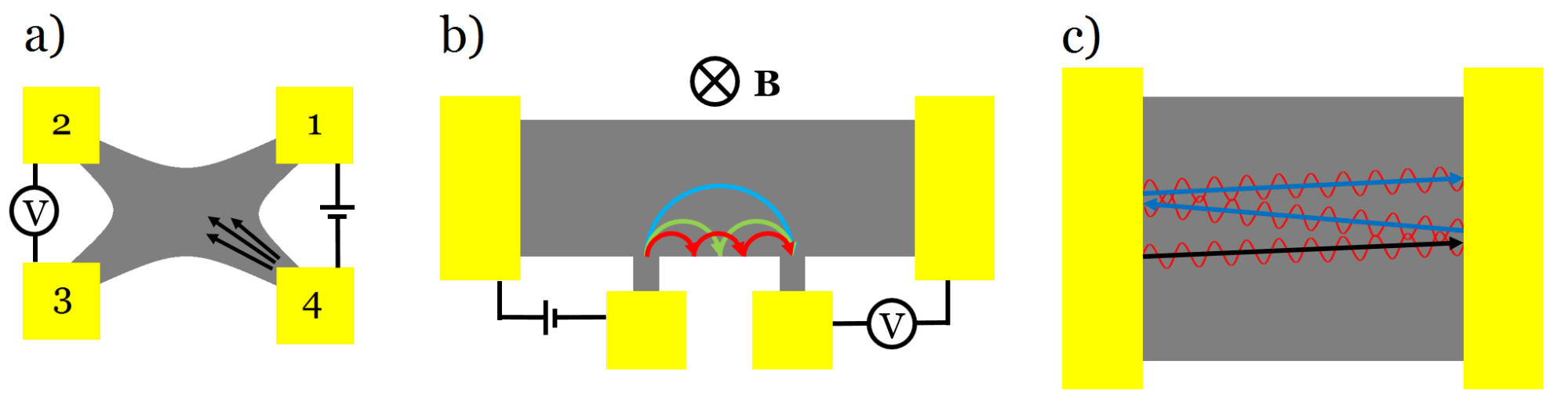
1. ábra a) A 4-es elektródából induló, a grafénon egyenesen áthaladó elektronok a 2-esben halmozódnak fel, ami feszültségméréssel detektálható, akár szobahőmérsékleten is. [1], [2] b) Mágneses fókuszálás: merőleges mágneses térben az elektronok kör alakú ciklotronpályára kényszerülnek. A szomszédos keskeny elektródába megfelelő mágneses térben éppen belepattog egy elektron, feszültségcsúcsot okozva.[3] c) Elektronhullámok interferenciája: a Fabry-Pérot jelenséghez hasonlóan a (vezetékeken) visszaverődő elektronok interferálnak egymással. A hullámhossz és a minta hosszának arányától függően a hullámok erősítik vagy kioltják egymást, növelve vagy csökkentve az áramot.[4], [T1], [T2]
A kutatás célja, a megválaszolandó kérdések
A kutatás célja a ballisztikus Dirac-elektronok viselkedésének megértése volt. Az ehhez szükséges nagy tisztaság akkor érhető el, ha a grafén fel van függesztve, evégett a bázeli kutatókkal együtt egy speciális mintakészítési eljáráson dolgoztunk [T3]. A ballisztikus elektronok viselkedését egy egyszerű szerkezetben, alsó kapuelektródák segítségével létrehozott p-n átmenetben vizsgáltuk.
A grafén és a két kapuelektróda (a 2. ábra sárga vezetékei) kondenzátorként viselkednek. Ha az elektródákra pozitív feszültséget kapcsolunk, a kialakult elektromos tér a felettük lévő grafénba elektronokat vonz, elektrontöbblet jön létre, míg negatív feszültség elektronhiányt (pozitív töltéssűrűséget) okoz. Ha a két elektródára ellentétes feszültséget kötünk, a negatív elektróda feletti grafénszakaszban pozitív, míg a pozitív elektróda feletti másik szakaszban negatív töltéssűrűség lesz (a 6. a) ábra p és n régiói), egy félvezető p-n átmenethez hasonlóan.
A p-n átmeneten mozgó elektronok viselkedésének megértése végett a rendszeren átfolyó áramot a sűrűségek és a mágneses tér függvényében mértük.

2. ábra A kapuelektródák (sárga) felett a vezetékekre (szürke) felfüggesztett grafén sematikus ábrája, illetve hamisszínes elektronmikroszkópos képe. A skála 1 mikron (µm).[T3] Az egyik elektródára negatív, a másikra pozitív feszültséget kapcsolva a felettük lévő grafénszakaszokban pozitív (p oldal), illetve negatív töltéssűrűség alakul ki (n oldal). A kettő között (a kék régió felett) a sűrűség pozitívból negatívba megy át.
Módszerek
Mintakészítés [T3]
Ballisztikus vezetés csak jó minőségű grafénban tapasztalható. A grafént általában hordozórétegre, legtöbbször szilícium-dioxidra helyezik, azonban ennek töltött szennyezői és rácshibái befolyásolják a grafénbeli elektronokat, tönkretéve a ballisztikus mozgást. Emellett a grafén felületét szerves vegyületek szennyezik, melyektől úgy szabadulhatunk meg, ha nagy áramsűrűséggel felfűtjük. Azonban a hordozó a hő egy részét elvezeti, csökkentve a tisztítás hatékonyságát.
A legjobb minták felfüggesztéssel készíthetők: így megszabadulunk a hordozó befolyásától, és a tisztítás során jobban felfűthetjük a grafént.
Először elektronsugaras litográfiával (EBL) alsó kapuelektródákat fabrikálunk.

3. ábra EBL: szigetelő felületre polimert (PMMA-t) viszünk fel, és a kiválasztott területet fókuszált elektronnyalábbal megvilágítjuk (exponálás). A PMMA szerkezete ettől megváltozik, megfelelő vegyszerrel kioldható (előhívás), így itt fedetlenné válik a szelet. Párologtatás útján fémréteget választhatunk le, ami a polimer feloldása után csak ezen a területen marad ott.
A szeletet egy polimerrel (LOR) vonjuk be, erre kerül a grafén (4. ábra), amelyre litográfiával vezetékeket fabrikálunk. A felfüggesztés is litográfiával történik: a grafén alatti LOR-t exponáljuk, így előhívás után a grafén a vezetékekre lesz felfüggesztve.
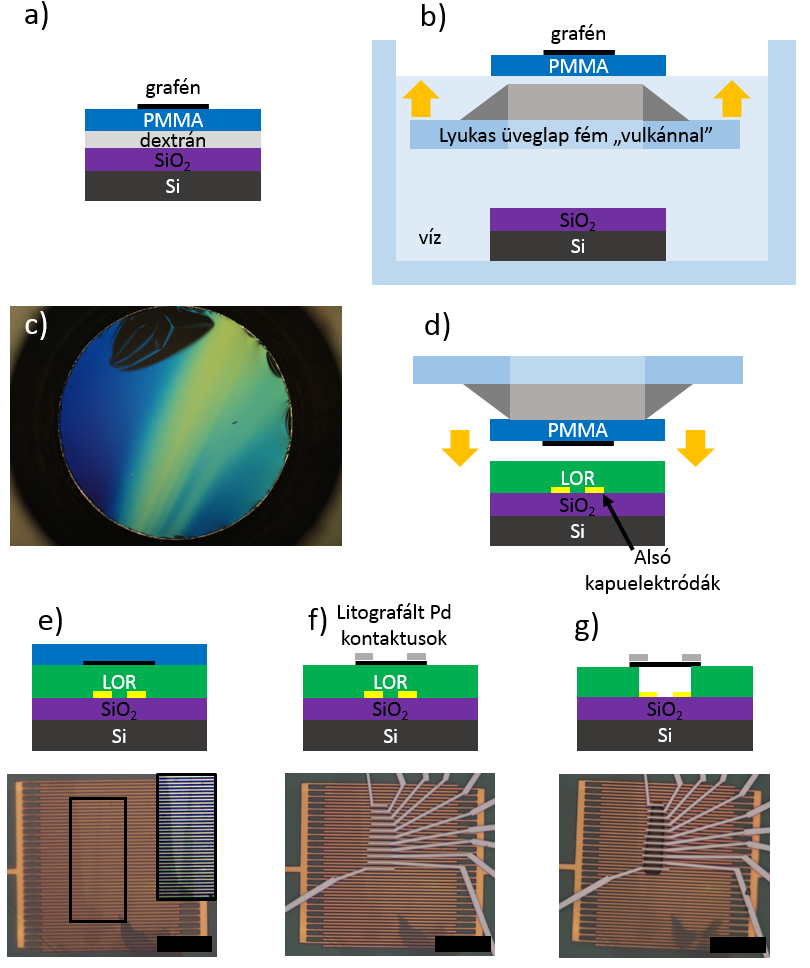
4. ábra a) A grafént grafitból, hámozással állítjuk elő: ragasztószalaggal letépünk néhány réteget, és a felületre nyomjuk. Az odatapadt grafén néhány tíz mikronos kristályait optikai mikroszkóp alatt keressük meg, ugyanis megfelelő hordozón látható kontrasztot ad, noha egyetlen atom vastagságú.[5] Valószínűtlen, hogy egy ekkora kristály éppen a kapuelektródák fölött tapadjon a LOR-ra, ezért a grafitos ragasztószalagot egy ideiglenes hordozóra, egy dextrán-PMMA kettősrétegre nyomjuk. b) Ezt vízre helyezve a dextrán feloldódik, és a vízfelületen úszó PMMA-t mikroszkóp alatt egy 3 mm-es fém “vulkánnal” kihalásszuk. c) Fénykép a vulkánról és a rátapadt hártyáról. A sötét folt gyűrődés, a grafén ilyen nagyításnál nem látható. d) A PMMA-t mikroszkóp alatt fejjel lefelé a 0,6 µm vastag LOR-ral bevont kapuelektródákra nyomjuk. A skála 20 µm. (e). A PMMA-t lemossuk, f) litográfiával elkészítjük a vezetékeket. g) Exponáljuk a grafén alatti LOR-t, és előhívjuk. Így kapjuk a kontaktusok között felfüggesztett grafént.[T3]
Méréstechnika
A méréseket kriosztátban, 1,5 K-en végezzük, különben az elektronok energiája, hullámhossza nem jól meghatározott. A kis zaj végett Lock-in technikával mérünk: 100 µV feszültséget adunk a mintára, az átfolyó áramot erősítő segítségével mérjük.
Tisztítás
A szerves szennyezők eltávolítása végett felhevítjük a (néhány µm-es) grafént, amihez nagy, akár 1 mA/µm áramsűrűséget használunk.
A bemutatott mérés olyan tiszta mintán született, amiben már 60 mT mágneses térben megfigyelhető a kvantált Hall-effektus, ami kiemelkedő minőségre utal.
Eddigi eredmények [T2]
A p-n átmenetet létrehozó kapuelektródák feszültségeit ellentétesen változtattuk (Ṽ, -Ṽ), az ezekkel arányos, grafénbeli két oldali töltéssűrűség is ellentétes volt (n, -n). A grafén sávszerkezete miatt az elektronhullám frekvenciája is ellentétes, ezért a csoportsebesség is megfordul.
Az elektronok merőleges B mágneses térben a sebességre merőleges Lorentz-erő miatt kör alakú, Rc sugarú ciklotronpályákra kényszerülnek. B növelésével ezek átmérője a minta mérete alá csökken, így a vezetékből kilépő elektronok a minta élén pattognak végig (5. ábra). A p-n átmeneten a Klein-alagutazás irányfüggése [4] miatt csak a közel merőlegesen érkező elektronok jutnak át. Az átmenet túloldalán Rc ugyanaz, de a csoportsebesség révén a Lorentz-erő is ellenkező irányú, így visszakanyarodnak a p-n átmenethez, és átérve megint az eredeti irányba kanyarodnak. Így kígyóznak a minta túlsó pereméig, ahol balra vagy jobbra pattognak tovább (6. a) vagy b) ábra), amit az határoz meg, hány félkörív fért el a minta szélességében. A tér és a sűrűség változtatásával a ciklotronsugár is változik (Rc arányos |n|0,5/B-vel), ezért az elektron felváltva az egyik, vagy a másik irányba fog továbbmenni. Ha visszajut a kiindulási elektródába, nem járul hozzá az áramhoz, ám ha a másikba kerül, növeli azt. Ezért ez az ún. kígyóállapot várhatóan az áram oszcillálásában fog megnyilvánulni. Ha B-t és n-t úgy változtatjuk, hogy a ciklotronátmérő (2Rc) állandó marad, és éppen páros vagy páratlan számszor fér el a minta W szélességében, arra számítunk, hogy az áram minimális/maximális: ez a B-n síkon parabolákat jelent (6. c) ábra).

5. ábra A ciklotron-félköröket leíró elektron a p-n átmenet két oldalán ellenkező irányba kanyarodik. Az átmenet mentén átkígyózik a túlsó peremre, és onnan folytatja útját.[T2]
Azonban a probléma ennél összetettebb, ugyanis a nem merőlegesen érkező elektronok is eljutnak a minta fenti pereméig: a p-n átmenetről visszaverődnek, a kezdő p oldalon maradnak, és úgy pattognak végig az átmeneten, mint eddig az alsó élen, és a fenti peremről visszaverődve átjuthatnak az n oldalra. Ráadásul a perem szabálytalanságai kiszámíthatatlan módon verhetik vissza a pályákat. Mindez elfedheti az 5. és 6. a), b) ábrákon vázolt mozgástól várt áramoszcillációt.
A 6. d) ábra az árammal arányos vezetőképesség színkódolt térképét ábrázolja, illetve annak feszültség szerinti deriváltját, a p-n átmenetet kialakító kapuelektródák egyikére kapcsolt Ṽ feszültség és a B tér függvényében (a másik elektróda -Ṽ feszültségű). Oszcillációk mintázata látható, ami a várthoz hasonló: a vezetőképesség parabolák mentén állandó, melyeken a ciklotronsugár (és viszonya a szélességhez) állandó. A kígyóállapotok járuléka tehát nem mosódik el, a fenti leírás jól illik a megfigyelt vezetőképesség-oszcillációkra.
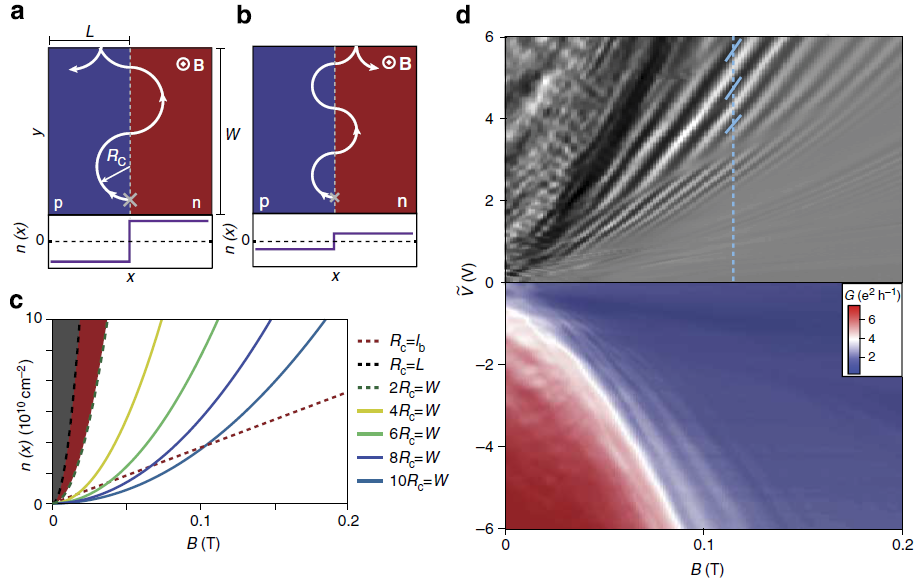
6. ábra a), b) A kígyóállapot csökkenti vagy növeli az áramot aszerint, hogy az Rc ciklotronsugár hogyan viszonyul a W szélességhez. c) Az összefüggő vonalak mentén Rc, ezért várhatóan az áram és vezetőképesség is állandó. d) Alul a vezetőképesség, felül ennek Ṽ feszültség szerinti deriváltja látható, Ṽ (mellyel arányos n) és a B tér függvényében. A vezetőképesség oszcillációinak mintázata megfelel a c) panel jóslatának. Ha egy félkör nagyobb a szélességnél, eltűnik a jelenség (2Rc>W, a c) panel piros és szürke tartományai). Ha viszont Rc kisebb a ciklotronpályák szélességénél (Rc<lB, a piros szaggatott vonaltól jobbra), már nem beszélhetünk ciklotronpályákról, és megszűnnek az oszcillációk .[T2]
Várható impakt, további kutatás
A grafén kiváló alapanyag az elektronoptikai vizsgálatokhoz, ugyanis a ballisztikus mozgás szobahőmérsékleten is megmaradhat [2]. A Klein-alagutazás irányfüggését [4] kihasználva olyan eszközök analógjai készíthetők belőle, mint a tükör, vagy az optikai szál. Az egyszerű geometriák kiismerése után nagyobb rendszereket állíthatunk össze, melyekben komplex kísérletek végezhetők. Mindez kikövezi az utat az elektronoptikai elemek kifejlesztésére, és új kaput nyit a nanoelektronikában.
A grafén a spintronika számára is ígéretes. Ez az ágazat az elektron mágneses momentumát, avagy spinjét használja fel információtárolásra és logikai műveletekre. Ultratiszta grafénban ballisztikus spintronikai kísérleteket lehetne folytatni, ami ezidáig felderítetlen világ.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk:
[T1] M.-H. Liu, P. Rickhaus, P. Makk, E. Tóvári, R. Maurand, F. Tkatschenko, M. Weiss, C. Schönenberger, K. Richter: Scalable tight-binding model for graphene, Phys. Rev. Lett. 114, 036601 (2015)
[T2] P. Rickhaus, P. Makk, M.-H. Liu, E. Tóvári, M. Weiss, R. Maurand, K. Richter, C. Schönenberger: Snake trajectories in ultraclean graphene p-n junctions, Nature Communications 6, 6470 (2015)
[T3] R. Maurand, P. Rickhaus, P. Makk, S. Hess, E. Tóvári, C. Handschin, M. Weiss, C. Schönenberger: Fabrication of ballistic suspended graphene with local gating, Carbon 79, p 486 (2014)
Más hivatkozások:
[1] D.-K. Ki, A. F. Morpurgo: High-quality multiterminal suspended graphene devices, Nano Letters, 2013, 13 (11), p 5165
[2] A. S. Mayorov, R. V. Gorbachev, S. V. Morozov, L. Britnell, R. Jalil, L. A. Ponomarenko, P. Blake, K. S. Novoselov, K. Watanabe, T. Taniguchi, A. K. Geim: Micrometer-scale ballistic transport in encapsulated graphene at room temperature, Nano Letters, 2011, 11 (6), p 2396
[3] T. Taychatanapat, K. Watanabe, T. Taniguchi, P. Jarillo-Herrero: Electrically tunable transverse magnetic focusing in graphene, Nature Physics 9, 225–229 (2013)
[4] P. Rickhaus, R. Maurand, M.-H. Liu, M. Weiss, K. Richter, C. Schönenberger: Ballistic interferences in suspended graphene, Nature Communications 4, 2342 (2013)
[5] P. Blake, E. W. Hill, A. H. Castro Neto, K. S. Novoselov, D. Jiang, R. Yang, T. J. Booth, A. K. Geim: Making graphene visible, Appl. Phys. Lett. 91, 063124 (2007)
[6] S. Morikawa, S. Masubuchi, R. Moriya, K. Watanabe, T. Taniguchi, T. Machida: Edge-channel interferometer at the graphene quantum Hall pn junction, Appl. Phys. Lett. 106, 183101 (2015)
[7] T. Stegmann, D. E. Wolf, A. Lorke: Magnetotransport along a boundary: from coherent electron focusing to edge channel transport, New J. Phys. 15, 113047 (2013)
Nem tudományos publikáció online:
http://index.hu/tudomany/2015/03/05/uttoro_grafenkutatasban_vettek_reszt_magyar_kutatok/
Linkgyűjtemény:
A nem tudományos hivatkozások nagy része a Wikipediára, vagy a Fizipediára hivatkozik.
