Oláh György Doktori Iskola 

BME VBK, Szervetlen és Analitikai Kémia Tanszék

Témavezető: Dr. Csonka Gábor István

Sűrűségfunkcionálok alkalmazása szerves és biomolekulákra 

A kutatási téma néhány soros bemutatása

Doktori kutatásom célja elektronsűrűségen alapuló elméleti módszerek fejlesztése, tesztelése és alkalmazása szerves és biomolekulák szerkezetének és gyenge kölcsönhatásainak vizsgálatára. Pályázatomban a sűrűségfunkcionál módszerek fejlesztésének aktuális kérdéseit és a nehezen számítható gyenge kölcsönhatások leírására komplex vegyületekben és kémiai reakciókban történő alkalmazási lehetőségeit mutatom be. Munkám során számos kérdésre sikerült nagy pontosságú megoldásokat szolgáltatnom időben hatékony módszerek segítségével, és eredményeim széles körben alkalmazhatók új összetett kölcsönhatások és bonyolult reakciók tervezésére, modellezésére.

 

A kutatóhely rövid bemutatása

Témavezetőmnek számos jelentős publikációja született a sűrűségfunkcionál-elmélet és a gyenge kölcsönhatások számítása területén [1–9]. Kutatócsoportunk sűrűségfunkcionál-elméleti témákban együttműködik a philadelphiai Temple University John P. Perdew által vezetett Anyagtudományi Központjával. A közös eredmények magas impakt faktorú folyóiratokban jelentek meg, és kiemelkedően magas idézettséget vontak maguk után. Jelenleg közreműködünk továbbá az MRCC kvantumkémiai szoftver tesztelésében is Kállay Mihállyal, a BME Fizikai Kémia és Anyagtudományi Tanszék Spektroszkópia Csoportjának vezetőjével.

 

A kutatás történetének, tágabb kontextusának bemutatása

Ioncsatornák és ionreceptorok

A szintetikus ioncsatornák a sejtmembránba mesterségesen beépíthető ioncsatornák, melyek tulajdonságait elméleti módszerekkel modellezni, tervezni lehet. Az adott ionra szelektív szintetikus ioncsatornák várhatóan új útját nyitják meg az egyetlen molekula érzékelésére alkalmas technikáknak. A szelektivitás az adott ion és egy tervezett fizikai-kémiai tulajdonságokkal bíró pi-rendszer közötti kölcsönhatáson alapszik. Hasonlóképpen, szelektív kation vagy anion receptorok állíthatók elő szupramolekuláris kémiai módszerekkel, melyeknek szenzorikai alkalmazása lehetséges. A kation-pi kölcsönhatásokkal ellentétben az anion-pi kölcsönhatások [10] pontos és gyors számítása az irodalomban mindeddig nem volt megoldott.

 

 

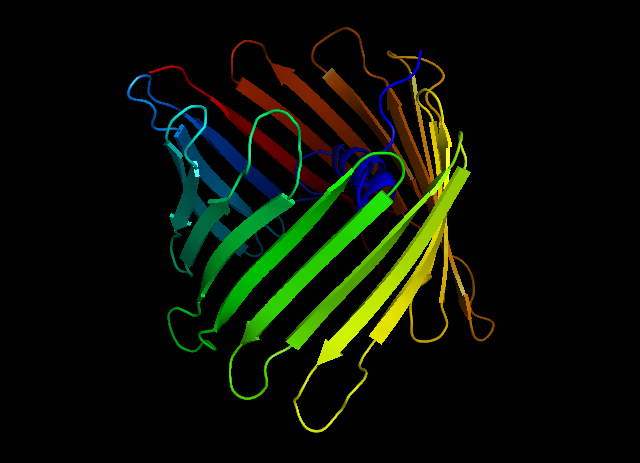
Humán feszültségfüggő nem szelektív anion csatorna (balra) és a szelektív szintetikus anion csatornához vagy receptorhoz szükséges anion-pi kölcsönhatások modellezése (jobbra)

 

Diels-Alder reakciók

A Diels-Alder reakciók a kémia számára alapvető jelentőséggel bíró gyűrűképzési reakciók; a névadó kutatók 1950-ben kaptak Nobel-díjat a felfedezésért. E reakciók az elméleti kémiában a sűrűségfunkcionálok delokalizációs hibája kapcsán kerültek előtérbe [11]. Ez azonban abból a félreértésből származik, hogy a kémiai értelemben vett delokalizáció megszűnése a reakció során felbomló konjugált rendszerrel lokalizáltabb elektronsűrűséget eredményezne. A Diels-Alder reakciók ezzel szemben kiváló lehetőséget nyújtanak az összetett intramolekuláris kölcsönhatások tesztelésére, ugyanis a mono-, bi- és triciklikus termékekben kialakuló kölcsönhatások leírását az elektronfelhők nemkötő átlapolása nehezíti. A Diels-Alder reakció energiák pontos és gyors számítása az irodalomban eddig még nem volt megoldott.

 

 

 

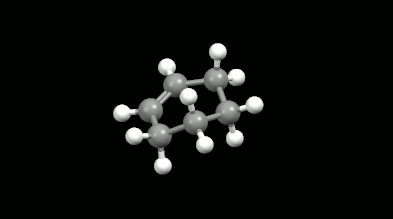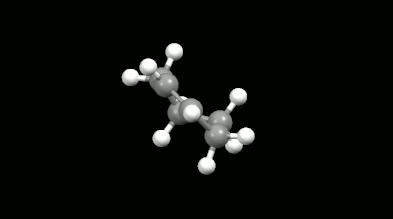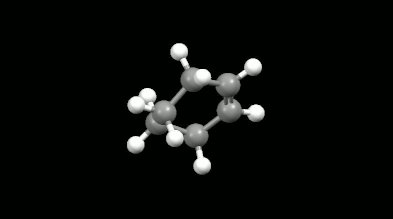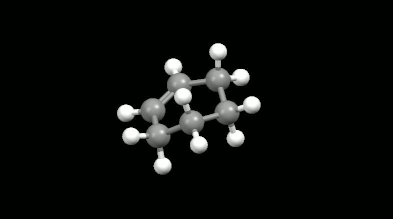
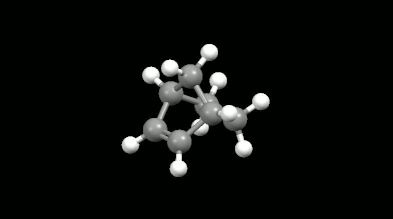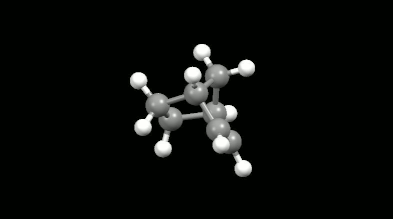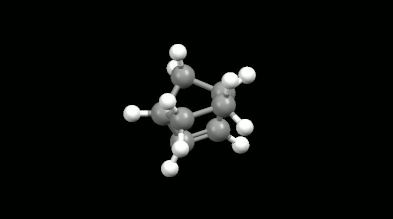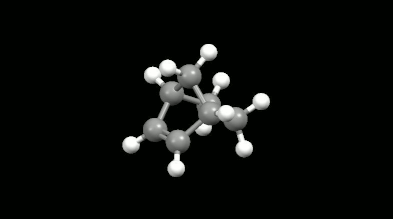
Diels-Alder reakciók mono- és biciklikus gyűrű illetve kalitka alakú termékei

 

A kutatás célja, a megválaszolandó kérdések.

Módszerfejlesztés a számításos kémiában

        A számításos kémiai módszerekkel szemben kétfajta elvárás van: legyen a módszer pontos és gyors. A pontosság egyszerre jelent helyességet és precizitást. Kémiailag pontosnak mondható egy módszer, ha legfeljebb 1 kcal mol-1 hibát vét a kémiai rendszerek energiájának számításában. A gyorsaság értelmezhető egy adott méretű rendszer esetében a számítási időn keresztül, de az összehasonlításhoz fontos a számítási idő skálázódása is a rendszer méretének növekedésével. A kifejlesztett módszer hatékonynak mondható, ha egyszerre pontos és gyors. A mérési módszerekhez hasonlóan az elméleti kémiai módszereket is tesztelni, validálni kell. A hatékonyság meghatározása az elméleti kémiai gyakorlatban előforduló problémák alapján összeállított tesztadatbázisok segítségével történik. A legismertebb ilyen adatbázis, a GMTKN30 a főcsoporti elemekből álló vegyületek termokémiáját, reakciókinetikáját és nemkovalens kölcsönhatásait teszteli [12].

 

Gyenge kölcsönhatások számítása

        A kémiai rendszerekben jelenlévő erős kovalens kölcsönhatások lokalizáltabb elektronsűrűséget eredményeznek, így a szemilokális sűrűségfunkcionál módszerek jobban képesek kezelni ezeket. A kölcsönhatás gyengülésével diffúzabbá váló elektronsűrűség miatt egyre inkább előtérbe kerül a sűrűségfunkcionálok delokalizációs hibája (többelektronos önkölcsönhatási hiba). Alapvető problémát okoz továbbá a nagyobb távolságokon keresztül ható gyenge diszperziós kölcsönhatások nemlokális természetének leírása a szemilokális sűrűségfunkcionál módszerekkel. A probléma megoldását azonban tovább nehezíti, hogy a kölcsönhatási és reakció energiák lehetnek igen összetettek, valamint a delokalizációs és diszperziós hibák gyakran egyszerre jelentkeznek.

 

Módszerek

Miért éppen sűrűségfunkcionál-elmélet?

Az elméleti kémiában az atomok és molekulák fizikai és kémiai tulajdonságait a Schrödinger egyenlet közelítő megoldásaiból számíthatjuk (mivel egzakt megoldás csak a legegyszerűbb rendszerekre lehetséges). A kémia számára érdekes rendszerek hullámfüggvénye az elektronok számának növekedésével egyre kezelhetetlenebbé válik, így a hullámfüggvény módszerektől eltérő, más megközelítés szükséges. Kézenfekvő a sokváltozós hullámfüggvény helyett a mindössze háromdimenziós elektronsűrűség-függvény használata. A sűrűségfunkcionál-elmélet hatékonyságát az adja, hogy egyelektronos sajátérték egyenletek (ún. Kohn-Sham egyenletek) segítségével lehet számolni [13]. A Kohn-Sham potenciál a magok által kialakított külső potenciálból, az elektronok közötti átlagos taszító Hartree potenciálból, valamint a kicserélődési és korrelációs potenciálból tevődik össze. Utóbbi nem ismert, a gyakorlatban azonban a kicserélődési és korrelációs potenciálokat együtt közelítik.

 

Sűrűségfunkcionál közelítések

A sűrűségfunkcionál közelítések hierarchiáját Perdew szerint a sűrűségfunkcionálok ún. Jákob létráján lehet ábrázolni [14]. A történet szerint Jákob álmában egy olyan létrát látott, mely felért a mennyországig, és az angyalok fel-alá közlekedtek rajta a föld és a mennyek között. A történet hasonló, mivel bár a sűrűségfunkcionál-elmélet egzakt módon van megfogalmazva, az egzakt funkcionál csak a kutatók álmaiban előttük lebegő cél. A létra jól ábrázolja a közelítések hierarchiáját, mivel felfelé haladva egyre nő a módszerek pontossága és ezzel együtt számítási ideje is, amint a közelítések egyre több információt vesznek figyelembe. A kutatók az angyalokhoz hasonlóan másznak fel a létrán, és a megoldandó problémától függően választanak a különböző szintű módszerek közül.

 

A sűrűségfunkcionál közelítések “Jákob létrája”

(LSDA: lokális spinsűrűségi közelítés, GGA: általánosított gradiens közelítés, MGGA: meta-GGA, HGGA: hiper-GGA, RPA: random-fázis közelítés)

 

Eddigi eredmények

Pontos intermolekuláris kölcsönhatási energiák

Az összetett intermolekuláris kölcsönhatások pontos számítását kettős és hármas anion-pi komplexek példáján mutatom be. A kettős komplexek esetében nagy pontosságú (DLPNO-CCSD(T)/CBS és LPNO-CEPA1/aug-cc-pVTZ) kölcsönhatási energiákat számítottam. Ezzel összehasonlítva a korábbi eredményeket [15] kimutattam, hogy az irodalomban eddig használt referencia módszer (MP2/6-31++G(d,p) + CP korrekció) tulajdonképpen alig jobb, mint a Hartree-Fock módszer, így alkalmatlan referenciának.

 

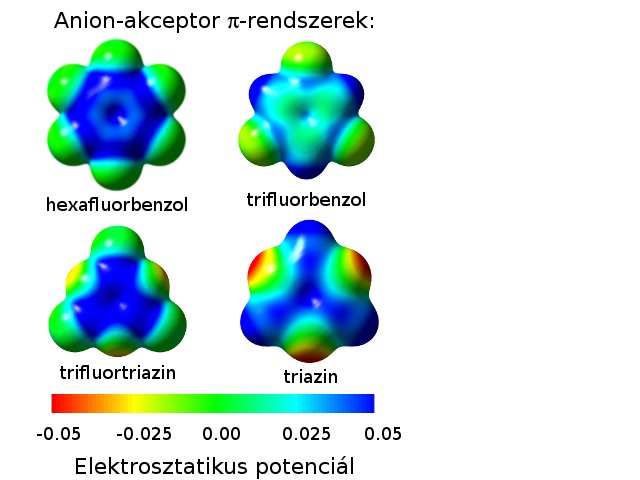
Anion-pi kölcsönhatások kialakulásának lehetőségei a pi-rendszer tekintetében

(A kék színnel jelzett régiók pozitív elektrosztatikus potenciálúak, így a negatív töltésű ionokkal vonzó elektrosztatikus kölcsönhatást képesek kialakítani.)

 

Az új referencia energiákhoz viszonyítva meghatároztam a diszperziót is figyelembe vevő különböző szinteken lévő fontosabb módszerek teljesítőképességét az anion-pi kölcsönhatások leírására. Kimutattam, hogy az RPA módszeren kívül egyik sűrűségfunkcionál módszer sem képes kellő pontosságú anion-pi kölcsönhatási energiákat szolgáltatni. A hármas komplexekhez új, pontos RPA referencia energiákat szolgáltattam a sűrűségfunkcionálok további fejlesztéséhez, teszteléséhez.

 

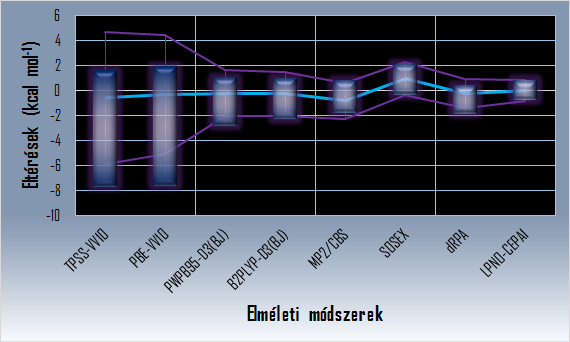
Különböző módszerekkel számított anion-pi kölcsönhatási energiák eltérése a referenciától (MP2 módszer kivételével ATZ bázis alkalmazása mellett)

(Az eltérések tartománya kék dobozzal, az átlagos eltérés világoskék vonallal, két szórásnyi környezete lila vonalakkal van jelölve.)

 

Pontos intramolekuláris kölcsönhatási energiák

Az összetett intramolekuláris kölcsönhatások pontos számítását a ciklikus termékekre vezető Diels-Alder reakciók példáján mutatom be. A GMTKN30-DARC adatbázisból [11, 12] származó referencia energiákhoz (CCSD(T)/CBS) viszonyítva meghatároztam a különböző szinteken lévő diszperziót is figyelembe vevő sűrűségfunkcionál módszerek teljesítőképességét. Kimutattam, hogy az RPA módszeren kívül egyik sűrűségfunkcionál módszer sem képes pontos Diels-Alder reakció-energiákat szolgáltatni.

 

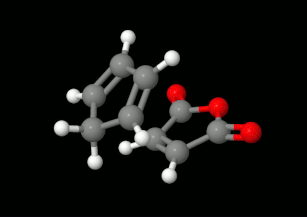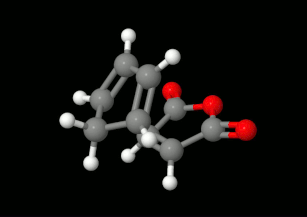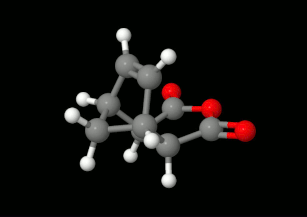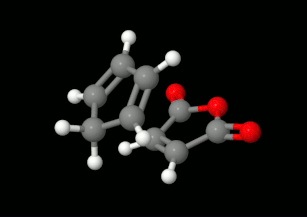
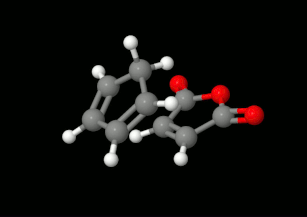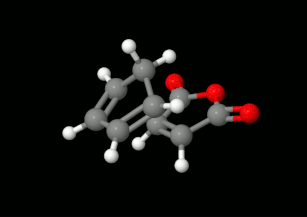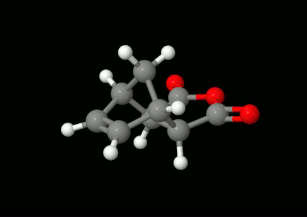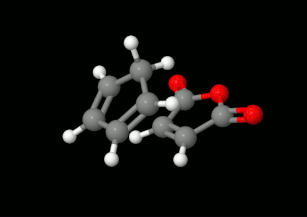
Diels-Alder reakciók modellezése: triciklikus termék kialakulásának lehetőségei

(balra: endo konformáció, jobbra: exo konformáció)

 

Kimutattam továbbá, hogy az egzakt kicserélődés növelésével a diffúzabb elektronsűrűséggel rendelkező rendszerek energiája nagyobb mértékben mélyül, és mivel a reakció energiák összességében exoterm irányba tolódnak el,  a feltételezettel ellentétben a termékekben a diffúzabb elektronsűrűség a kicserélődési-korrelációs lyuk nagyobb fokú delokalizációjával jár.

 

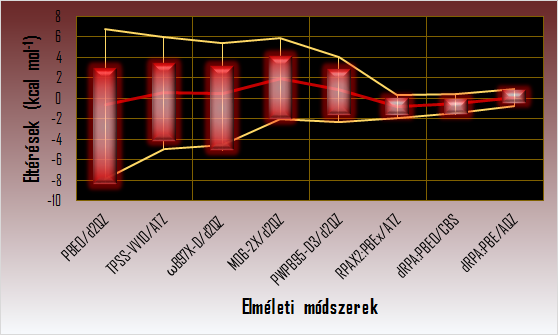
Különböző módszerekkel számított Diels-Alder reakció-energiák eltérése a referenciától

(Az eltérések tartománya piros dobozzal, az átlagos eltérés piros vonallal, két szórásnyi környezete sárga vonalakkal van jelölve.)

 

Új hatékony teljes bázis extrapoláció

A direkt RPA korrelációs energia lassú báziskonvergencia problémáját megoldva létrehoztam egy kisebb bázisokat használó teljes bázisextrapolációs sémát, mellyel az irodalomban használt nagy pontosságú extrapoláció [16] eredményei nagyságrendekkel rövidebb idő alatt elérhetők. Az eljárás azon a felismerésünkön alapszik, hogy a különböző összetételű és szerkezetű molekulák korrelációs energiája a bázisméret növekedésével az irodalomban feltételezett állandó kitevőjű inverz köbös kifejezés helyett különböző kitevőjű hatványfüggvény szerint konvergál.

 

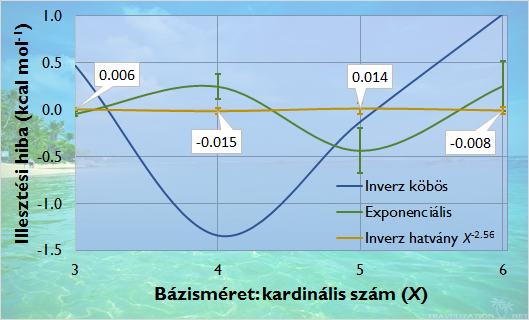
Direkt RPA korrelációs energia konvergenciája a bázisméret növekedésével különböző függvényekkel közelítve

(65 szénhidrogén izomerre vett átlagos illesztési hiba, aug-cc-pVXZ bázisok alkalmazásával)

 

A dRPA korrelációs energia báziskonvergenciáját meghatároztam 65 szénhidrogén molekula esetében (CH4 összegképlettől C6H6 összegképletig) korreláció-konzisztens aug-cc-pVXZ bázisok segítségével (X = T, Q, 5, 6). A hatványfüggvény kitevőjét a molekulában lévő összes atom számosságához viszonyított atomi hozzájárulásokból, vagy pontosabban a szerkezeti információt is hordozó hibridállapotokból lineáris kombinációval közelítettem.

 

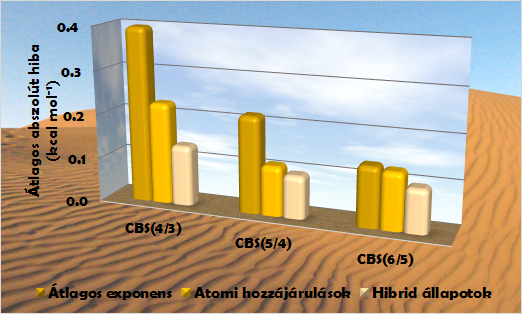
Teljes bázis-extrapolációs módszerek hibája

(65 szénhidrogén izomerre vett átlagos abszolút hiba, aug-cc-pVXZ bázisok alkalmazásával)

 

Új saját duális hibrid RPA módszer

Kifejlesztettem továbbá egy újfajta duális hibrid direkt RPA módszert (dRPA75), mely jól teljesít a molekuláris fizikai kémia több területén is. A módszer 75% egzakt kicserélődést tartalmazó PBE hibrid pályákon számolja a dRPA korrelációs energiát (ez előnyös a szerves molekuláknál fellépő többelektronos önkölcsönhatási hiba csökkentése szempontjából [17, 18]), és ehhez az egzakt kicserélődési energia helyett a hibrid kicserélődési energiát párosítja. A kifejlesztett módszerem teljesítőképességét reakció energiákat, aktiválási gátakat és nemkovalens kölcsönhatási energiákat tartalmazó tesztadatbázisokon határoztam meg dupla hibrid és más RPA módszerekkel összehasonlítva.

 

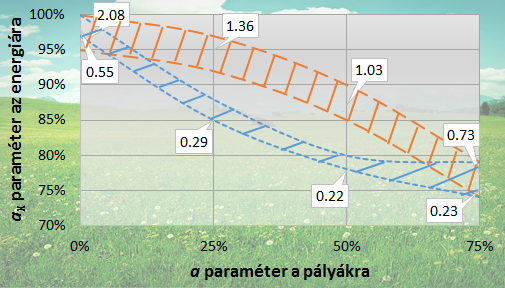
Paraméter-optimálás a duális hibrid (dRPA75) funkcionál kifejlesztéséhez

 

(A narancssárga hosszú szaggatott vonallal határolt terület az aktiválási energia számára, a kék rövid szaggatott vonallal határolt terület a reakció energiák számára kedvező paraméter tartomány. Szövegbuborékokban a lokálisan minimális átlagos abszolút hibák kcal mol-1 egységekben.)

 

Az új módszer a párkölcsönhatásokon alapuló diszperzió korrigált funkcionálokkal ellentétben képes megragadni a nemkovalens kölcsönhatások nem páronkénti jellegét. Univerzálisan használható minden típusú intra- és intermolekuláris kölcsönhatásra. Ugyanakkor jobban teljesít reakcióenergiákra , mint a dupla hibrid módszerek és pontosabb a hidrogéntranszfer aktiválási gátakra, mint a drágább RPAX2 módszer [19].

 

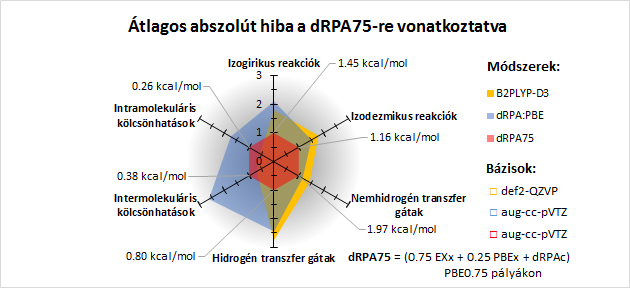
Az új duális hibrid módszer (dRPA75) teljesítőképessége reakció energiákra, gátakra és gyenge kölcsönhatásokra

 

Várható impakt, további kutatás

        Eredményeim a magas impakt faktorú Journal of Chemical Theory and Computation folyóiratban publikálom (IF: 5.498). Az anion-pi kölcsönhatásokról szóló cikkünkben [S1] szolgáltatott részletes elemzés és a nagy pontosságú referenciaenergiák alapjául szolgálhatnak új sűrűségfunkcionálok fejlesztéséhez, teszteléséhez. A Diels-Alder reakciókról szóló cikkünk [S2] összehasonlítja a sűrűségfunkcionálok delokalizációs és diszperziós hibáinak javítási lehetőségeit. Az általam kifejlesztett teljes bázis-extrapolációs módszer [S3] nagyságrendekkel rövidebb idő alatt megoldja az RPA korrelációs energia lassú konvergenciájának problémáját, így lehetőséget nyújt nagyobb molekulák pontosabb számítására is. Az általam kifejlesztett duális hibrid RPA módszer [S4] kiválóan teljesít a molekuláris fizikai kémia számos területén, módszeremet az MRCC kvantum kémiai szoftverben implementálták. A továbbiakban ezen módszer szélesebb körű alkalmazásán és továbbfejlesztésén fogok dolgozni.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Saját publikációim:

[S1] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A.; Sun, J. J. Chem. Theory Comput. 2015, 11, 360–371.

[S2] Mezei, P. D.; Csonka, G. I.; Kállay, M. J. Chem. Theory Comput. 2015, 11, 2879–2888.

[S3] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A. J. Chem. Theory Comput. 2015 most elfogadott, online közzétéve. ct–2015–00269g

[S4] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A.; Kállay, M. J. Chem. Theory Comput. 2015 felülvizsgálaton. ct–2015–00420z

 

Linkgyűjtemény:

Kohn Nobel-díj előadása a sűrűségfunkcionál-elmélet kifejlesztéséért

Tony Cheetham és John Perdew interjúja Walter Kohnnal

Perspektíva: sűrűségfunkcionál-elmélet 50 éve a kémiai fizikában – szerző: Becke 

Sűrűségfunkcionál-elmélet kihívásai – szerzők: Cohen, Mori-Sánchez és Yang

Sűrűségfunkcionál-elmélet aktuális korlátai – szerzők: Cohen, Mori-Sánchez és Yang

 

Hivatkozások:

[1] Perdew, J.; Ruzsinszky, A.; Csonka, G. I.; Vydrov, O.; Scuseria, G.; Constantin, L.; Zhou, X.; Burke, K. Phys. Rev. Lett. 2008, 100, 136406.

[2] Ruzsinszky, A.; Csonka, G. I.; Scuseria, G. E. J. Chem. Theory Comput. 2009, 5, 763–769.

[3] Perdew, J. P.; Ruzsinszky, A.; Csonka, G. I.; Constantin, L. A.; Sun, J. Phys. Rev. Lett. 2009, 103, 026403.

[4] Ruzsinszky, A.; Sun, J.; Xiao, B.; Csonka, G. I. J. Chem. Theory Comput. 2012, 8, 2078–2087.

[5] Perdew, J. P.; Ruzsinszky, A.; Tao, J.; Staroverov, V. N.; Scuseria, G. E.; Csonka, G. I. J. Chem. Phys. 2005, 123, 62201.

[6] Steinmann, S. N.; Csonka, G. I.; Corminboeuf, C. J. Chem. Theory Comput. 2009, 5, 2950–2958.

[7] Ruzsinszky, A.; Perdew, J. P.; Csonka, G. I. J. Chem. Theory Comput. 2010, 6, 127–134.

[8] Ruzsinszky, A.; Perdew, J. P.; Csonka, G. I. J. Chem. Phys. 2011, 134, 114110.

[9] Csonka, G. I.; French, A. D.; Johnson, G. P.; Stortz, C. A. J. Chem. Theory Comput. 2009, 5, 679–692.

[10] Schottel, B. L.; Chifotides, H. T.; Dunbar, K. R. Chem. Soc. Rev. 2008, 37, 68–83.

[11] Johnson, E. R.; Mori-Sánchez, P.; Cohen, A. J.; Yang, W. J. Chem. Phys. 2008, 129, 204112.

[12] Goerigk, L.; Grimme, S. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688.

[13] Kohn, W.; Sham, L. J. Phys. Rev. 1965, 140, A1133–A1138.

[14] Perdew, J. P.; Schmidt, K. AIP Conf. Proc. 2001, 577, 1–20.

[15] Garau, C.; Frontera, A.; Quiñonero, D.; Russo, N.; Deya, P. M. J. Chem. Theory Comput. 2011, 7, 3012–3018.

[16] Fabiano, E.; Della Sala, F. Theor. Chem. Acc. 2012, 131, 1278.

[17] Sai, N.; Barbara, P. F.; Leung, K. Phys. Rev. Lett. 2011, 106, 226403.

[18] Atalla, V.; Yoon, M.; Caruso, F.; Rinke, P.; Scheffler, M. Phys. Rev. B - Condens. Matter Mater. Phys. 2013, 88, 1–8.

[19] Heßelmann, A. Phys. Rev. A 2012, 85, 012517.