Doctoral School of Mathematics and Computer Science 

Department of Stochastics / Mathematical Institute

Supervisor: Dr. Károly Simon

Asymptotic behaviour of shortest paths in random graphs

 Introducing the research area

In the past few decades the better understanding of large complex networks has become increasingly important in numerous different fields. Different random graph models serve as  mathematical objects trying to capture the different properties of these networks. One of the main goals of my research is to see which models exhibit the so-called "small-world" property and what consequences can be drawn from it.

Brief introduction of the research place

I have done my PhD studies at the Stochastics Department under the supervision of Dr. Károly Simon. Numerous members of the faculty are internationally acclaimed researchers in their respective fields. The MTA Stochastic Research Group is in close cooperation, many invited speakers from abroad give seminar talks at the Stochastic and Dynamical Systems seminars and we have a number of ongoing TAMOP and OTKA grants at the department.

History and context of the research

Often we say: “It’s a small world.”- when two people suddenly find some seemingly distant mutual friend. Indeed, it is often observed that in real world networks only a few connections  are needed to get from one place to another. The theory of random graphs models such large networks, which has become a very dynamically developing branch of applied probability.

The seminal work [10] of Pál Erdős and Alfréd Rényi in the early 1960’s set forth the theory of random graphs. In their model for any pair of vertices we independently flip a (biased) coin and we draw an edge between them if and only if the result is heads. They showed that the model has the "small world" property, which mathematically put says that the shortest paths in the graph scale logarithmically with the number of vertices.

However, the model doesn’t possess other typical properties of complex networks such as a power-law degree distribution, large clustering, inhomogeneity or hierarchical structure [2,5,6,7,13,14]. Hence, numerous new models were defined lately.

Finding shortest paths is a classical graph theoretical problem, which is efficiently solvable algorithmically. For random graphs it is possible to exactly determine the expected length of the shortest paths simply from the dynamics of the model without ever having to simulate one. Presently this is a very challenging and popular topic [1,3,4,5,7,9,11,12] which is one of my research areas. 

 

The research goal, open questions

One of the main goals of random graphs is to introduce models that capture the properties of some real world network and yet are simple enough to be analysed analytically. In my research I’ve studied two models in detail:

1. Inhomogeneous random graph (IHRG)[5]: can be considered as a natural generalization of the Erdős-Rényi model. Each vertex is given a type, chosen randomly from some finite set and for each pair we choose a different coin to flip according to the types. The strength of the model is that many others are special cases of it since there is a great freedom in choosing the parameters. The figure below shows an IHRG with three types consisting of 50, 100 and 300 vertices.
    

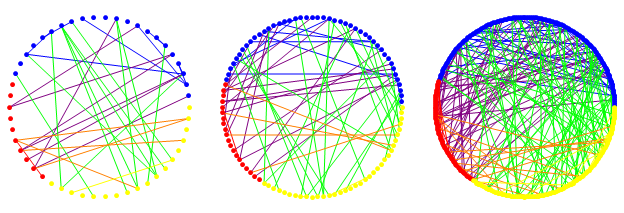
2. Random Apollonian network (RAN)[13,14]: the graph originates from Apollonian’s  circle packing problem, which is simple to generate in two dimensions. Starting from a triangle, in each step repeat the following: choose a triangle uniformly at random, insert a vertex inside it and connect it with the vertices of the chosen triangle. The model can readily be generalized to arbitrary d-dimensions with d-dimensional simplices.

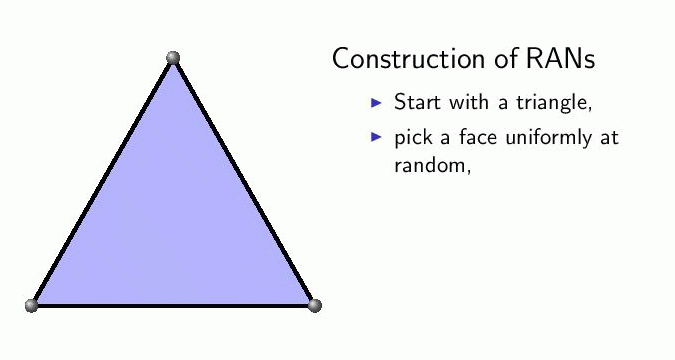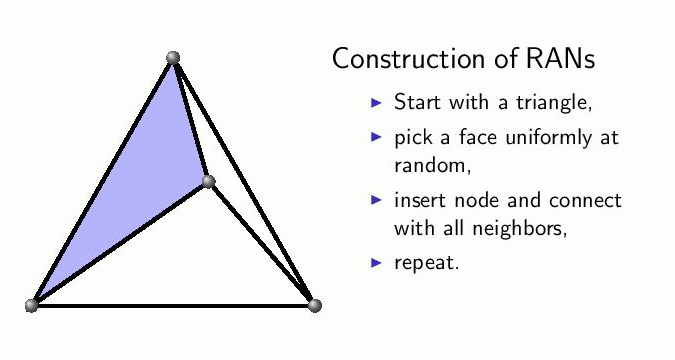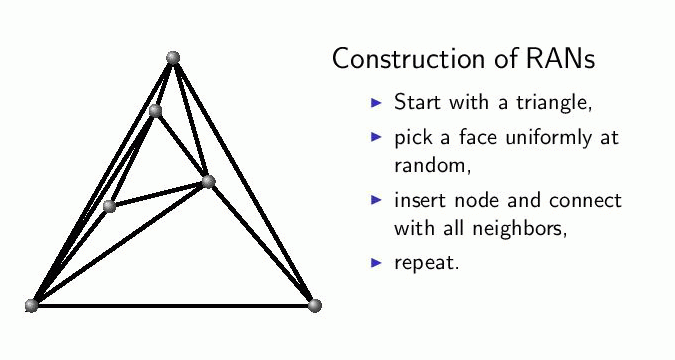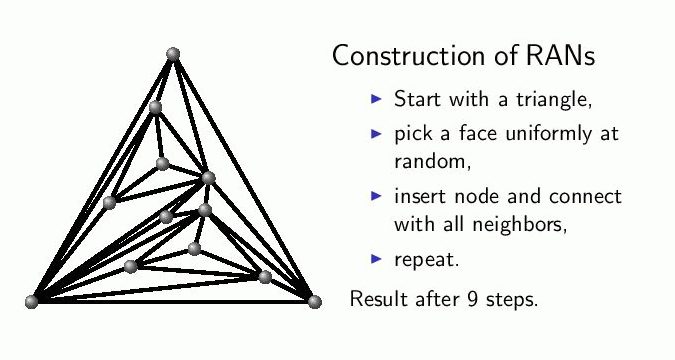
In graphs with edge weights we wish to determine the weight of the shortest-weight path and the number of edges, termed hopcount, on this path (which coincide when there are no edge weights). There are three main questions to ask:

1. What is the weight/length between two uniformly chosen vertices?

2. What is the flooding time of a random vertex (the maximal shortest path from a fixed vertex)?

3. What is the diameter of the graph (that is the maximal flooding time)?

We studied the IHRG with exponential edge weights and the RAN without weights. The main goal was to show the "small world" property.

Methods

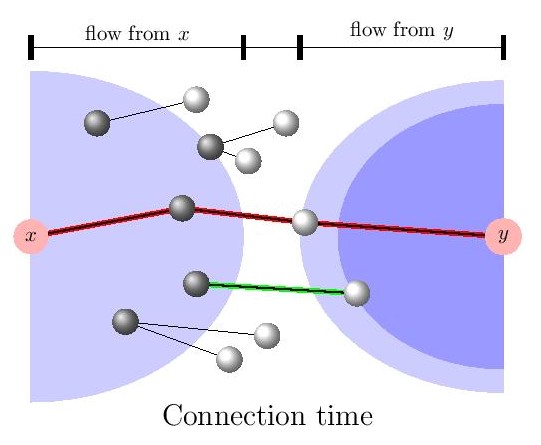
The heuristics of the proofs are not difficult to follow, however, the precise formalism needs the application of several different methods. The exploration process initiated from a vertex can be best visualized as a flow of fluid which runs at a constant speed on the edges started from the vertex. When the flow reaches another vertex, then the shortest path has been found between them and the time taken gives the length/weight of the path. It is more practical to start a flow from both vertices simultaneously and wait until they collide.

It often occurs in large graphs that the beginning of an exploration process shows a tree structure, i.e. there are no cycles. If the distribution of the neighbors of a vertex is known, then locally this exploration process can be coupled to a continuous time branching process (BP). Hence, we can directly apply results from the extensive literature of BPs. This is the case for the IHRG, but for RANs they appear in a different way.

The collision of the two flows presents the greatest challenge. We can not follow the flows in continuous time, but only in discrete steps as new vertices are reached by the flows. The shortest path is potentially found when each flow reaches a vertex  that have an edge between them (green edge in figure). It’s only a potential candidate, though, since a little later we may find two similar vertices through which the path is shorter (red path in figure). Thus the shortest path is the minimum of these candidates.

Further technical difficulties arise from handling the different types and our theorems hold for much more general type-spaces which are proved by careful approximations by finite types.

RANs are far from being locally acyclic. Instead we can use its hierarchical structure to our advantage. To each vertex a unique code can be assigned from which its neighbors can be exactly determined. Hence, an appropriate grouping of the edges reveals a tree-like structure of the graph.

One group of edges can be identified yet again with a continuous time BP, since the discrete evolution of the graph can be embedded into a continuous time process. The typical and deepest branch of the BP needs to be determined. With the other edges we can take “shortcuts”, whose distribution leads to the coupon collector’s problem in probability theory. The proof also uses renewal theory, large deviation theory, method of moments and solves a conditional extreme point problem.

The analytical methods were complemented by simulations, which helped formulate conjectures and later confirmed our results.

Results

We showed the small world property for both models, i.e. the quantities of interest scale logarithmically with the number of vertices (denoted by ) in the graph.

In the IHRG model the hopcount, between two vertices chosen uniformly at random, after proper standardization follows a central limit theorem (CLT) as  tends to infinity. Thus the magnitude of the expected hopcount and also its standard deviation can be exactly determined. Namely, the former is  while the latter is , where the constants and are deterministic constants, independent of the realization, derived from the parameters of the graph. Similarly, the weight of the path is , where   is deterministic and is a random constant. These results generalize the ones of [4] concerning the Erdős-Rényi model.

A CLT also holds for RANs. The hopcount and the weight coincide, since there are no edge weights. The magnitude of the expected value is  and the standard deviation is , where the constants again are deterministic, independent of the realization. To the best of our knowledge this is the first case without edge weights where a CLT was proven.

Furthermore, we showed that the flooding time and the diameter of the graph also scale logarithmically, also determining the exact constants. This is a tougher task, in many models the constants  are not known. Independent of our work, others [8,9] also studied RANs with different methods, however ours gave the most general results.

The lemma describing the connection process has an important corollary [K14]. Simply put, it states that only  vertices are traversed by the two flows if they are started simultaneously. On the other hand, this is  when only one exploration process is initiated. As a result, the search for the shortest path takes instead of the  time only  time for the IHRG and even much faster  for RANs. We conjecture that this phenomenon generally holds for small worlds.

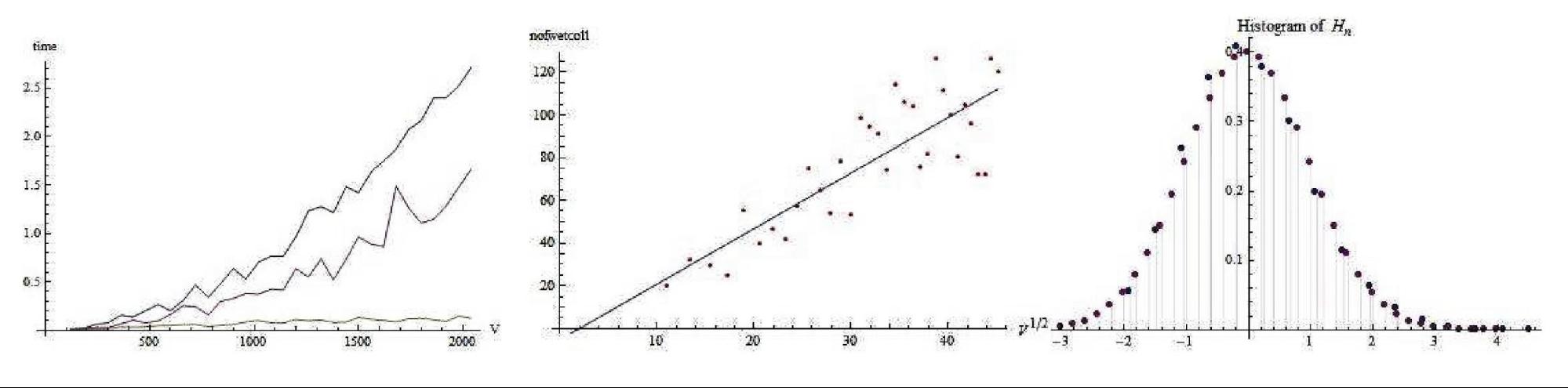
Extensive simulations nicely confirm our analytical results. The left figure shows the significant difference in the running time in favor of case with two flows. In the middle we can see that the number of vertices explored is indeed basically proportional to . In the right one we can see the nice bell-shaped curve of the histogram of the hopcount for a graph with only 270 vertices.

 

 

Expected impact and further research

These results were presented in various forms; as talks given at international conferences or seminars and as posters at a workshop. The article about the IHRG [KK15] just appeared in the journal Advances in Applied Probability. In this same journal the article about RANs [KKV15] was just accepted. Both already have a few independent citations.

I’ve been awarded a young researcher position at the MTA Alfréd Rényi Institute of Mathematics, where I will join the Limits of Structures Lendület research group this September. This is a great opportunity to continue my research in this direction. I also plan to stay active in my other fields of interest like graph limits [KR11], fractals [BK15], renewal processes [KT11].

 

Publications, references, links

Publications.

[KK15] I. Kolossváry, J. Komjáthy (2015). First Passage Percolation on Inhomogeneous Random Graphs. Advances in Applied Probability 47, 589-610.  

[KKV15]  I. Kolossváry, J. Komjáthy, L. Vágó (2015). Degrees and distances in random and evolving Apollonian networks. accepted in Advances in Applied Probability.  

[K14] I. Kolossváry (2014). Some consequences of the connection of exploration processes in small worlds. Technical report, preprint.

[BK15] B. Bárány, I. Kolossváry (2015). On the absolute continuity of the Blackwell measure. Journal of Statistical Physics 159, 158-171.

[KR11] I. Kolossváry, B. Ráth (2011). Multigraph limits and exchangeability. Acta Mathematica Hungarica 130, 1-34.

[KT11] I. Kolossváry, M. Telek (2011). Explicit Evaluation of ME(3) Membership. QUEST 2011: Fast Abstracts, CTIT Workshop Proceedings Series WP11-03, 11-12.

 

Links.

Posters on the topic: IHRG, RAN.

Curriculum Vitae

 

References.

[1] H. Amini, M. Lelarge (2015). The diameter of weighted random graphs. Ann. Appl. Probab. 3, 1686–1727.

[2] A.-L. Barabasi,  R. Albert (1999). Emergence of scaling in random networks. Science 286, 509-512.

[3] S. Bhamidi, R. van der Hofstad, G. Hooghiemstra (2010). First passage percolation on random graphs with finite mean degrees. Ann. Appl. Probab. 20(5), 1907-1965.

[4] S.Bhamidi, R. van der Hofstad, G. Hooghiemstra (2011). First passage percolation on the Erdős-Rényi random graph. Combinatorics, Probability and Computing 20, 683-707.

[5] B. Bollobás, S. Janson, O. Riordan (2007). The phase transition in inhomogeneous random graphs. Random Structures and Algorithms 31, 3-122.

[6] B. Bollobas, O. Riordan, J. Spencer, G. Tusnady (2001). The degree sequence of a scale-free random graph process. Random Structures and Algorithms 18, 279-290

[7] F. Chung, L. Lu (2003). The average distance in a random graph with given expected degrees. Internet Math. 1, 91–113.

[8] C. Cooper, A. Frieze, and R. Uehara (2014). The height of random k-trees and related branching processes. Random Struct. Alg. 45, 675-702.

[9] E. Ebrahimzadeh, L. Farczadi, P. Gao, A. Mehrabian, C. M. Sato, N. Wormald, J. Zung (2013). On the Longest Paths and the Diameter in Random Apollonian Networks. Electronic Notes in Discrete Mathematics 43, 355-365.

[10] P. Erdős, A. Rényi (1960). On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17-61.

[11] C. D. Howard (2004). Models of first-passage percolation. In Probability on Discrete Structures, Springer, Berlin, pp. 125–173.

[12] S. Janson (1999). One, two and three times log n/n for paths in a complete graph with random weights. Combinatorics, Probability and Computing 8(4), 347-361.

[13] Z. Zhang, L. Rong, F. Comellas (2006). High-dimensional random Apollonian networks. Physica A: Statistical Mechanics and its Applications 364, 610-618.

[14] T. Zhou, G. Yan, B.-H. Wang (2005). Maximal planar networks with large clustering coefficient and power-law degree distribution. Phys. Rev. E 71, 046141.