BME Vásárhelyi Pál Építőmérnöki és Földtudományi Doktori Iskola  

BME Építőmérnöki Kar, Hidak és Szerkezetek Tanszék

Témavezető: Dr. Katula Levente

Egyhéjú, szabad formájú acél rúdszerkezetek avagy rácsos héjak 

A kutatási téma néhány soros bemutatása

Az egyhéjú acél rúdszerkezetek, más néven rácsos héjak az utóbbi másfél évtizedben igen közkedvelt szerkezettípussá váltak (1. ábra). Főként az ún. szabad-formájú, vagyis (látszólag) szabálytalan alakú lefedő szerkezetek terjednek el, elsősorban az építészeti ábrázolást segítő programok fejlődésének köszönhetően. Ám a geometriai komplexitás miatt a szerkezettervezés és a gazdaságos építés terén több speciális kérdés vetődik fel. Kutatásom egyik fő célkitűzése a geometria és a szerkezet erőjátéka közötti kapcsolat feltérképezése. A másik fő cél a rudakat összekötő kapcsolatok vizsgálata. Részletes numerikus számítást dolgoztam ki, mely segítségével különböző geometriájú és különböző kapcsolattal megépült rácsos héjak szerkezeti viselkedését hasonlítom össze.

 

 

1. ábra: Magyarországon megépült rácsos héjak: felül: Bálna (Budapest, egyrétegű, szabad formájú); középen: Párizsi Nagy Áruház üvegkupolája (Budapest, egyrétegű, szabad formájú); Zsolnay Kulturális Negyed hídja (Pécs, kétrétegű, forrás), alul: Bikás park metró megálló lefedése (Budapest, egyrétegű, szabad formájú, forrás); Xantus János gömbkilátó (Balatonboglár, egyrétegű, szabályos gömb)

A kutatóhely rövid bemutatása

A Hidak és Szerkezetek Tanszék az Építőmérnöki Kar szerkezettervezést oktató egysége, magasépítési tartószerkezetek és hídszerkezetek kutatásával foglalkozik. Számos hazai kiemelt projektben (pl. Pentele híd, Hárosi híd) szerepel szakértőként, társtervezőként vagy független ellenőrként. Többnyire alkalmazott kutatás folyik: vékony falú acélszerkezetek, acélszerkezetek stabilitása, földrengés, vasbeton előregyártott gerendák, stb. Mindezekhez segítséget nyújtanak a tanszék akkreditált szerkezetvizsgáló laboratóriumában végzett kísérletek.

A kutatás történetének, tágabb kontextusának bemutatása

A térbeli rácsos szerkezetek egyrétegű illetve két- vagy többrétegű rácsokra oszthatók fel. A 20. század második felében reneszánszát élő kétrétegű rács sík kialakítással is nagy fesztávolságú terek lefedésére alkalmas. Ezzel szemben az egyhéjú rácsos szerkezetek a terheket elsősorban a felület görbületének segítségével képesek felvenni. A túl lapos héjak a felületükre merőleges elmozdulásokat alig képesek meggátolni. Ez is jól mutatja, hogy a rácsos héjak szerkezeti viselkedésében meghatározó az alakjuk, és geometriai kialakításuk.

 

A héjszerkezetekről már Gaudi kutatásai óta tudjuk, hogy akkor lesz gazdaságos, ha a gyakran előforduló terhek hatására csak húzó- és nyomóerők keletkeznek a szerkezetben. Gaudi a szerkezetek alakját úgy vette fel, hogy láncokból megépítette a tervezendő szerkezet tükörképét: egy függesztett szerkezetet gravitációs terhekkel. Az így kialakult, csak húzóerőkkel működő alak fordítottja csak nyomást vesz fel. A héjszerkezetek gazdaságos tervezése napjainkban is ezen az egyszerű elven alapul. Gaudi példájához hasonlóan, a számítógépes tervezésben az ideális rácshéj alakot a csak húzással működő ponyvaszerkezetek tervezéséhez használt ún. alakkeresési algoritmusokkal határozható meg. Ilyen alakkeresési algoritmus a dinamikus relaxáció [1], melyet például a 2000-ben épült londoni British Múzeum udvarának lefedéséhez használtak [2], amely valószínűleg a szerkezettípus leghíresebb példája (2. ábra).

 

 

2. ábra: A forma létrehozása dinamikus relaxációval: British Múzeum (London, forrás); Amsterdam Maritime Múzeum (Amszterdam, forrás)

 

A kutatás célja, a megválaszolandó kérdések

Egyhéjú rácsos szerkezetek vizsgálatával számos kutatás foglalkozik, de elsősorban kupolákra, dongákra és elliptikus transzlációs felületekre koncentrálnak, míg szabad-formájú szerkezetekkel ritkán találkozhatunk. Kutatásom során a négyszög alaprajzra illeszkedő háromszög rácsozású héjakat vizsgálom. Kérdés, hogyan található meg az ideális forma (alak vagy topográfia és szerkezeti magasság) és az ideális rácshálózat sűrűség.

 

A rácsos héjak erőjátékának másik kulcsfontosságú része a kapcsolati kialakítás [G6]. A kétrétegű rácsok elemeit egyszerű, például egy csavarral kialakított kapcsolatok kötik össze, melyek általában elfordulásra képes, csuklós kapcsolatok. A lapos, egyrétegű rácsok a felületükre merőleges terheket csak akkor képesek viselni, ha az alkalmazott kapcsolat elfordulásra nem vagy csak részlegesen képes, más szóval hajlításra merev vagy félmerev viselkedésű. Ezt általában hegesztett vagy több csavaros kapcsolattal érik el, ami munka és anyagigényesebb a csuklós kapcsolatoknál. A szerkezettípus terjedése olyan gazdaságos kapcsolati rendszerek fejlesztését igényli, melyek a pontonként változó görbületű felülethez jól igazíthatók [3]. Akkor gazdaságos a szerkezet, ha a kapcsolat csak annyira merev, amennyire az adott szerkezet esetében szükséges. Ezt a rúdelemek keresztmetszetének (szelvényének) alakjával is elő lehet segíteni: a gyakorlatban elterjedt csőszelvényekhez képest az egyszeresen szimmetrikus például téglalap vagy T szelvények előnye, hogy a héj felületére merőlegesen nagyobb merevséget biztosítanak a szerkezetnek, mint a héjfelület síkjában. Kutatásom célja egy félmerev T szelvényű kapcsolat kidolgozása.

Módszerek

Kutatásom során a dinamikus relaxációhoz hasonló alakkeresési módszerrel [2] határoztam meg a négyszög alaprajzú szerkezetek alakját. Alakkeresés során a rácselemek helyére képzelt, egymáshoz képest elfordulni képes (csuklós) rugókból és a csomópontokon működő erőkből álló rendszer egyensúlyi alakját iteratív módon kapjuk meg (3. ábra). A rugók merevségeinek változtatásával könnyedén lehet egymástól kissé eltérő alakú szerkezeteket létrehozni (4. ábra), melyek teherbírásait később összevetettem. Az alak jellemzésére szolgáló R paraméter a különböző irányokba futó rugómerevségek arányát jelenti.

 

 

3. ábra: Alakkeresés a Kangaroo programmal

 

4. ábra: Az alakkeresés során a különböző irányba futó rugómerevségek változtatásával kapott alakok (R=0,3÷3)

 

Szerkezeti viselkedés szempontjából a rácsos héjak a diszkrét rúdszerkezetek és a folytonos (pl. vasbeton) héjak tulajdonságait egyaránt magukban hordozzák. Emiatt viselkedésük meglehetősen összetett, a geometriai tulajdonságoktól, merevségi viszonyoktól függően a szerkezetek a teherbírásukat többféle módon elveszíthetik [5,6] (5. ábra). A pingponglabda horpadásához hasonló a héjszerű horpadás, mely egyszerre több csomópontot érint, míg a többi tönkremeneteli mód akár egy csomópont tönkremenetelével is bekövetkezhet. Ezeket a tönkremeneteleket a stabilitáselmélet vizsgálja.

 

 

 

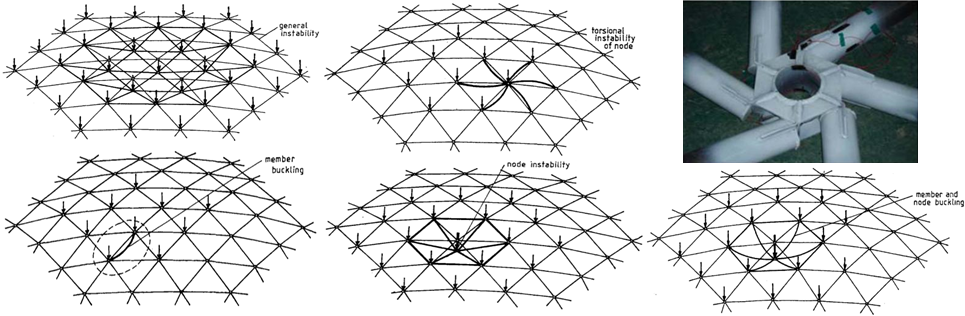
5. ábra: A rácsos héjak lehetséges tönkremeneteli módjai [5]: fent: héjszerű horpadás, csomópont elcsavarodása, csomópont elcsavarodása gyenge pengelemez miatt [7]; lent: rúdelem kihajlása, csomópont átpattanása, utóbbi kettő interakciója

 

A szerkezetek teherbírását szabványos terhek alapján, több mértékadó teherelrendezésre számítottam. A számítást numerikus modellen végeztem: nemlineáris végeselemes modellt építettem, melyek helyességét analitikus és kísérleti eredmények alapján igazoltam [G2]. A végeselemes modellben különösen fontos a szerkezet valós, tényleges viselkedését figyelembe vevő tökéletlenségek, ún. imperfekciók figyelembe vétele, melyre rácsos héjak esetén nincs szabványosított módszer. Az imperfekciók egyik fajtája geometriai jellegű: ilyenek pl. az építési pontatlanságok, hisz a szerkezetet lehetetlen pontosan az eredeti tervnek megfelelő geometriával megépíteni. Mivel a szerkezet alakja nagymértékben befolyásolja az erőjátékot [6], így már kis geometriai pontatlanság is jelentősen csökkenti a teherbírást [G4]. A figyelembe vett imperfekció alakjával és mértékével csupán néhány kutatás foglalkozik [8,9].

 

Kidolgoztam egy olyan parametrikus vizsgálati eljárást, mely a merev és félmerev kapcsolatú, különböző geometriájú szerkezeteknek nem csak a teherbírását ellenőrzi, hanem meghatározza a minimális szükséges szelvényméretet is, ezáltal kisebb súllyal tervezhető meg a szerkezet. A kidolgozott parametrikus vizsgálati eljárással eldönthető, hogy egy kapcsolattípus gazdaságosan alkalmazható-e adott fesztávolságú szerkezetek esetén. Ezen túl hálósűrűség, magasság-fesztávolság arány alapján eldönthető, hogy létezik-e olyan alak, melyre az adott csomóponttal a szerkezet képes viselni a terheket.

Eddigi eredmények

Az eddig elvégzett paraméteres vizsgálatokkal [G2] az L=20 méteres fesztávolságú szerkezeteket elemeztük. Egy kis merevségű ún. „socket” kapcsolatot alkalmaztunk [10], mely a csőszelvényű rúdelemeket egy 30 mm átmérőjű csavarral kötik be a csomóponti elembe. Az eredményekből látszik, hogy a vizsgált tartományban a közel azonos alakú szerkezetek bizonyultak a legjobb teherbírásúnak minden hálósűrűség és magasság esetén, ahogy az a 6. ábrán lévő táblázatban látható. Az R=4÷6 típusú alakok esetén adódtak a legkisebb szelvényátmérők (d), melyek egyben azok az alakok, ahol a szerkezet görbülete sehol sem túl kicsi.

 

Kimutattam, hogy kis imperfekciók (L/1000) esetén, a kapcsolat ezen a fesztávon (L) alkalmazható, vagyis mindig találhatunk egy olyan alakot, aminél a szerkezet képes viselni terheit. Ezzel szemben a 24 mm átmérőjű csavarral a lapos és nagy hálósűrűségű szerkezeteken már nem. Nagy imperfekciók (L/300) esetén már a 30 mm-es kapcsolat sem felel meg a lapos és nagy hálósűrűségű szerkezeteknél.

 

 

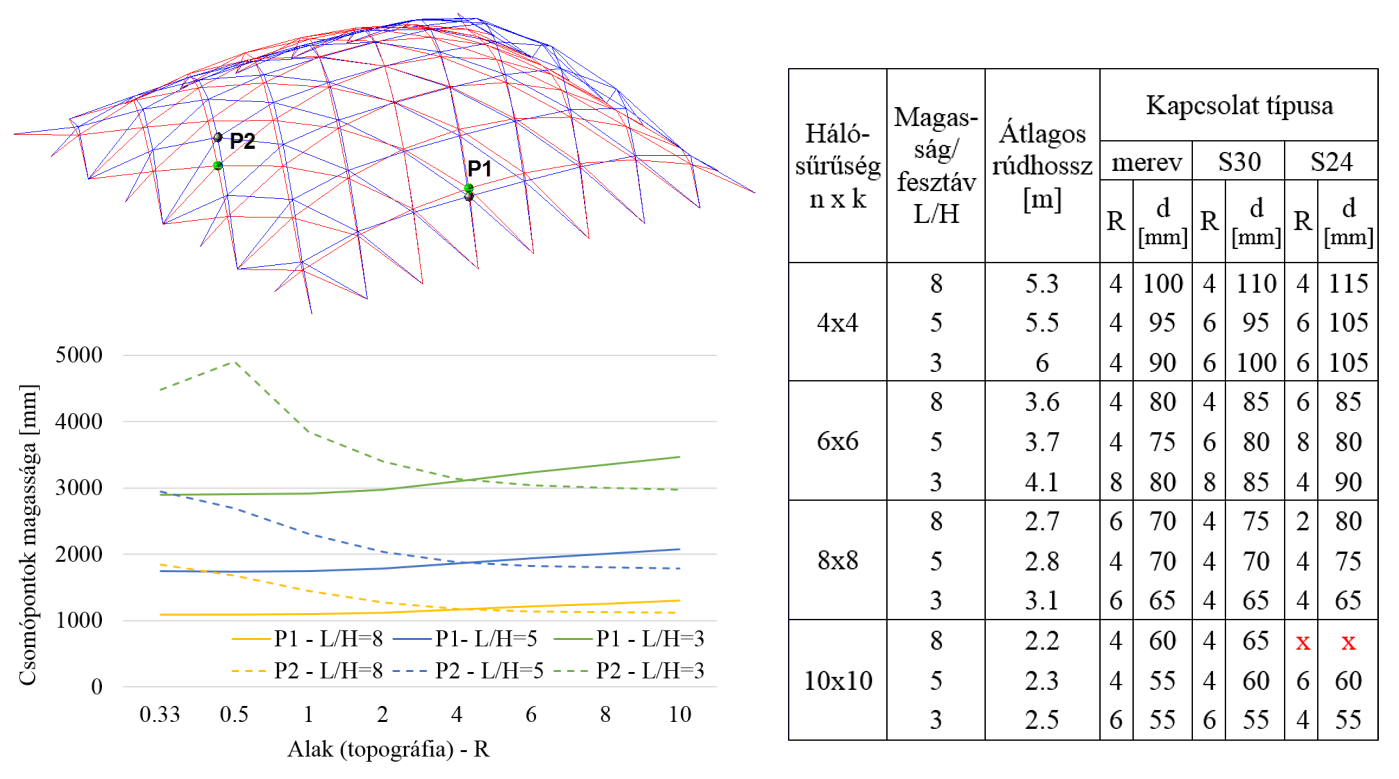
6. ábra: A különböző alakú szerkezetek összevetése; bal: az alakok geometriai jellemzői; jobb: analízis eredménye kis imperfekciók (L/1000) figyelembevételével, ahol d a megtervezett szerkezet szelvényátmérője

 

A kutatás során egy új csavarozott csomóponti rendszer fejlesztésével is foglalkozom (7. ábra), mely T keresztmetszetű rudakból álló szerkezeteknél alkalmazható (pl. Milánói Vásár lefedése). Az előző „socket” kapcsolathoz képest merevebb, nagyobb teherbírású, mivel két csavar rögzít egy rúdelemet, ezáltal nagyobb fesztávolságok lefedésére is alkalmas. A kapcsolati rendszer mérettől függően 3 különböző fesztávolság tartományban alkalmazható, melyhez először a T szelvény méreteit határoztam meg.  

 

 

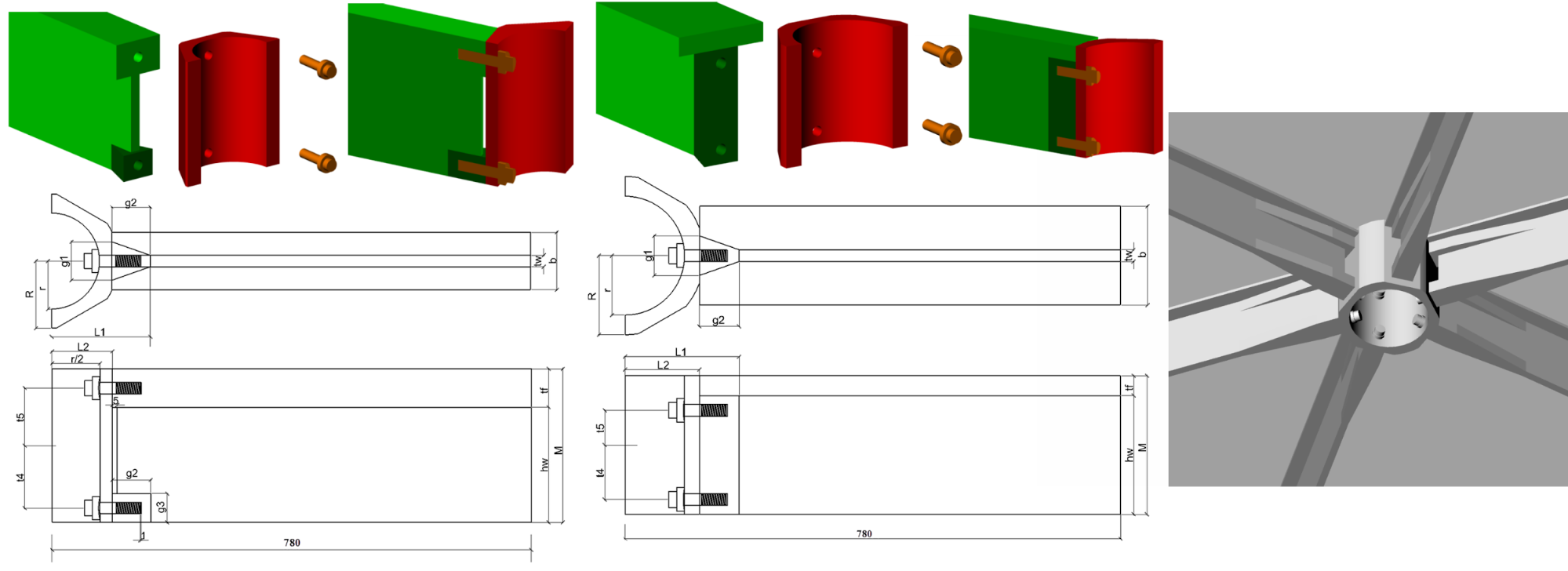
7. ábra: Új kapcsolati rendszer két kis mértékben eltérő kialakítással

 

A kapcsolat merevségét az előző végeselemes modellezésnél pontosabb és csak a kapcsolat környezetére kiterjedő ún. test végeselemes modellen (8. ábra) vizsgáltam. A modellben figyelembe vettem a csavar által kifejtett feszítőerőt, valamint ún. kontakt végeselemek segítségével azt, hogy az összefeszített, eredetileg érintkező felületek terhelés hatására megnyílhatnak, eltávolodhatnak egymástól. A kapcsolat méreteit a modellen végzett paraméteres vizsgálattal határoztam meg: a csavarátmérőt és a csavar fogadására alkalmas gúlaelem (7. ábrán sötétzöld) méreteit. A numerikus modell helyességét a kínai Harbini Műszaki Egyetem térbeli szerkezeteket kutató központjával folytatott közös kutatásban kísérletileg igazoltuk (9. ábra) [G1].

 

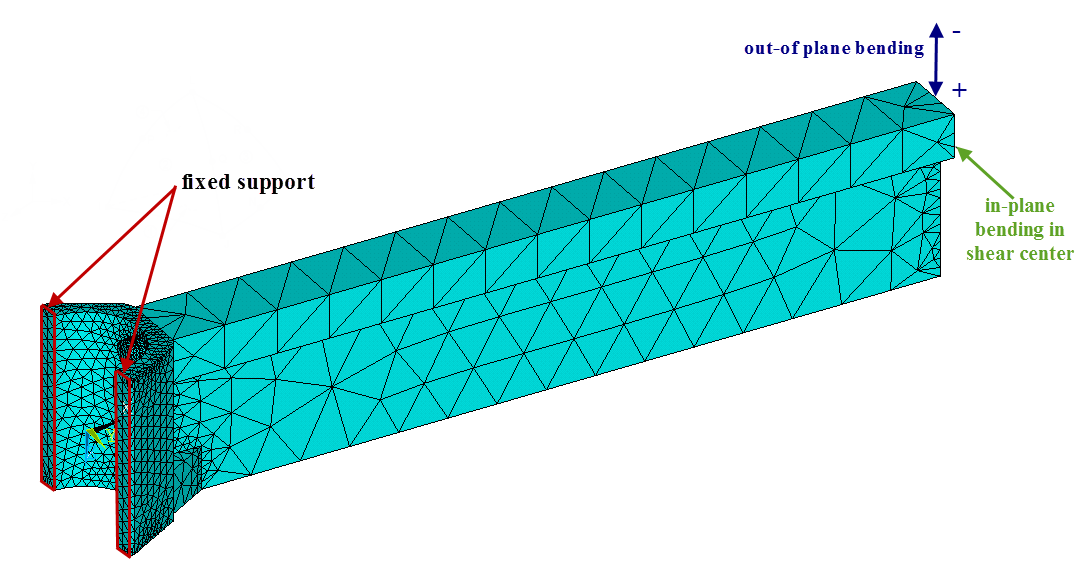
8. ábra: A kapcsolat végeselelemes modellje

 

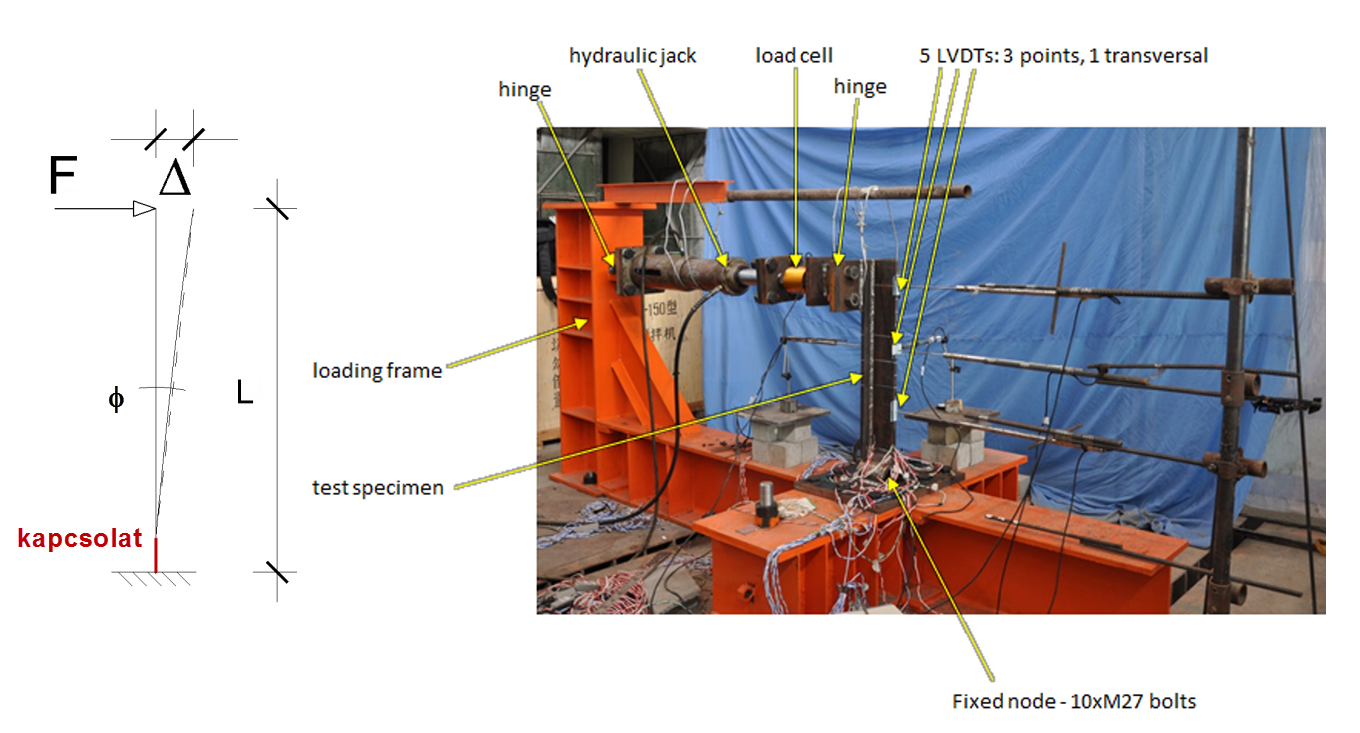
9. ábra: A kapcsolat hajlítási merevségének meghatározására végzett kísérlet

 

Várható impakt, további kutatás

A vizsgálat következő fázisában kiterjesztem a négyzet alaprajzú lefedés paraméteres vizsgálatát 20÷100 méteres fesztávolságokra. A cél a fentiekhez hasonló következtetések levonása, vagyis a kapcsolattípusok minősítése és a különböző alakzatok összevetése. Kisebb fesztávokon a „socket” típusú kapcsolat, nagyobb fesztávolságokon a T kapcsolatok alkalmazását tervezem. A szerkezetek teherbírásának számítása a T kapcsolatú szerkezeteknél az eltérő imperfekciók miatt is kihívást jelent.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája

 

[G1] Gidófalvy, K., Katula, L., and Ma, H., A semi-rigid steel joint system for free-form shell structures with T sections, Periodica Politechnica, 2015 (előkészületben)

 

[G2] Gidófalvy, K., Katula, L., and Ma, H., Semi-rigid joints in free-form grid shell structures, Journal of the International Association of Shell and Spatial Structures, 2015 (beadott)

 

[G3] Gidófalvy, K., Katula, L., Ma, H., and Fan, F., Semi-rigid free-form grid shells on rectangular plan, 7. European Conference on Steel and Composite Structures (Eurosteel 2014), Ed. Landolfo, Mazzolani, 2014

 

[G4] Gidófalvy, K., and Katula, L., Imperfection for the Buckling Analysis of Grid Shells, Proceedings of the Second Conference of Junior Researchers in Civil Engineering, 2013

 

[G5] Gidófalvy, K., Katula, L., and Mészáros, L., Behaviour study of single-layer steel grid shells based on numerical analysis, Proceedings of the Ninth FIB International PhD Symposium in Civil Engineering, Ed. Müller, Haist, Acosta, KIT Scientific Publishing, 2012, pp. 563–567.

 

[G6] Gidófalvy, K., and Katula, L., Effect of connection rigidity on the behaviour of single-layer steel grid shells, Proceedings of the Conference of Junior Researchers in Civil Engineering, 2012

 

[G7] Gidófalvy, K., Szabad formájú szerkezetek tervezése, MAGÉSZ Acélszerkezetek, Vol. 7, No. 2, 2010, pp. 41–45.

 

[G8] Gidófalvy, K., Szabad formájú szerkezetek tervezése, 14. Fémszerkezeti Konferencia, Göd, 2010, pp. 1–5.

 

Linkgyűjtemény

 

British Múzeum: A tervezés során szakértőként közreműködő Chris Williams professzor honlapján az alakkeresésről és a héjak viselkedéséről érdekes információk találhatók.

Térbeli rácsos szerkezetek – Dr. Hegedűs István egyetemi jegyzete

Ponyvaszerkezetek – Dr. Hegedűs István egyetemi jegyzete

Héjszerkezetek stabilitása – szemléletesen

 

Hivatkozások listája

 

[1] Alamatian, J., Displacement-based methods for calculating the buckling load and tracing the post-buckling regions with Dynamic Relaxation method, Computers and Structures, Vol. 114–115, 2013, pp. 84–97.

 

[2] Williams, C.J.K. (2001) ‘The analytic and numerical definition of the geometry of the British Museum Great Court Roof’, 434–440, Mathematics & design 2001, Burry, M., Datta, S., Dawson, A., and Rollo, A.J. eds. Deakin University, Geelong, Victoria 3217, Australia.

 

[3] Kilian, A., and Ochsendorf, J., Particle-spring systems for structural form finding, Journal of the International Association for Shell and Spatial Structures, Vol. 46, No. 2, 2005, pp. 77–84.

 

[4] Stephan, S., Sánchez-Alvarez, J., and Knebel, K., Stabwerke auf Freiformflächen (Reticulated structures on free-form surfaces), Stahlbau, Vol. 73, No. 8, 2004, pp. 562–572.

 

[5] Kato, S., Fujimoto, M., and Ogawa, T., Buckling Load of Steel Single-Layer Reticulated Domes of Circular Plan, Journal of the International Association for Shell and Spatial Structures, Vol. 46, No. 1, 2005, pp. 41–63.

 

[6] Gioncu, V., Buckling of reticulated shells. State-of-the-art, Int. Journal of Space Structures, Vol. 10, No. 1, 1995, pp. 1–46.

 

[7] Kim, Y.J., Lee, Y.H., Kim, H., Bending Test of Welded Joints for Single-Layer Latticed Domes, Steel Structures, Vol. 8, 2008, pp. 357–367.

 

[8] Bulenda, Th., and Knippers, J., Stability of grid shells, Computers and Structures, Vol. 79, 2001, pp. 1161–1174.  

 

[9] Fan, F., Yan, J., and Cao Z., Elasto-plastic stability of single-layer reticulated domes with initial curvature of members, Thin-Walled Structures, Vol. 60, 2012, pp. 239–246.

 

[10] Fan, F., Ma, H., Chen, G., and Shen, S., Experimental study of semi-rigid joint systems subjected to bending with and without axial force, Journal of Constructional Steel Research, Vol. 68, 2012, pp. 126–137.