Fizikai Tudományok Doktori Iskola 

BME TTK, Fizika Tanszék/Fizikai Intézet

Témavezető: Dr. Bokor Nándor

A fókuszfolt optimalizálása nagy numerikus apertúrájú rendszerekben 

A kutatási téma néhány soros bemutatása

Kutatásom középpontjában erősen fókuszált lézernyalábok fókuszfoltjának alkalmazásorientált optimalizációja és az optimális fókuszfolthoz tartozó megvilágítás megkeresése áll. Elméleti modelleket és numerikus algoritmusokat dolgoztam ki, melyek az eddig ismert módszereknél általánosabban és egyszerűbben alkalmazhatóak. Numerikusan stabil eljárást alkottam meg olyan újfajta függvényrendszerek kiszámítására, melyek más kutatási területeken, például a geofizikában is hasznosak lehetnek.

 

A kutatóhely rövid bemutatása

Munkámat a Fizika Tanszék Optikai Méréstechnika Csoportjában végzem, melynek a kutatási tevékenysége a koherens és inkoherens optikai méréstechnika, a holográfia és számítógépes képfeldolgozás mellett a nagy numerikus apertúrájú fókuszáló rendszerek vizsgálatára is kiterjed. Az ezzel kapcsolatos kutatómunkában együttműködő partnereink a japán Olympus Corporation és az izraeli Weizmann Intézet.

 

A kutatás történetének, tágabb kontextusának bemutatása

 

1. ábra: Konfokális pásztázó mikroszkóp használat közben: az erősen fókuszált lézernyalábok egyik gyakorlati alkalmazása [F1]

 

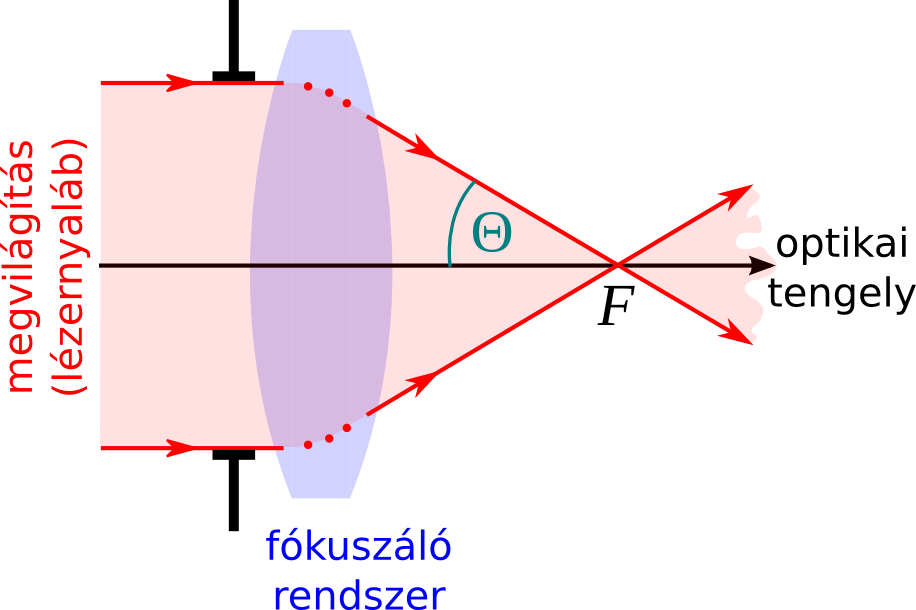
Az alkalmazott optikában számos olyan gyorsan fejlődő kutatási terület van – például a pásztázó lézeres mikroszkópia [1] (ld. 1. ábra), a nanorészecskék optikai csapdázása [2] vagy a nanolitográfia [3] –, melynél kiemelten fontos, hogy a fényt minél kisebb méretű foltra fókuszáljuk, illetve a fókuszfolt bizonyos jellemzőit (intenzitás- és polarizációeloszlás) kontrolláljuk. Ennek érdekében a megvilágító lézernyalábot ún. nagy numerikus apertúrájú (tipikusan NA > 0,6) optikai rendszerrel kell fókuszálni, ahol a NA értéke (levegőben) megegyezik a fókuszpontba érkező fénykúp Θ félnyílásszögének szinuszával (ld. 2. ábra). A gyakorlatban nagy NA-jú fókuszáló rendszerként jellemzően mikroszkópobjektíveket alkalmaznak.

 

 

 

A nagy NA-jú fókuszáló rendszerek elméletében a fizikai optika klasszikus közelítő módszerei (paraxiális közelítés, skalárdiffrakció) nem használhatóak, az elektromos és mágneses teret vektormezőkként kell kezelni. Leggyakrabban az ún. Debye–Wolf-féle vektor-diffrakcióelmélet [4, 5] használatos, azonban alternatív módszerként érdemes megemlíteni a fókuszálás multipólelméletét [6] is. Ez a fókuszmezőt – az elektromos mezőt a fókuszpont kicsiny, néhány hullámhossznyi környezetében – a multipólsugárzás elméletéből jól ismert vektor-multipólmezők lineáris kombinácójaként állítja elő.

 

Ismert megvilágítások fókuszmezejének a számolása mellett kiemelt fontosságú az inverz probléma is, vagyis az adott intezitás- és polarizációeloszlású fókuszfolthoz tartozó megvilágítás (elektromos térerősség-eloszlás) megkeresése. Bár speciális esetekre találhatóak az irodalomban megoldások [7-12], általánosan alkalmazható, az egész fókusztérfogatot tekintetbe vevő módszerről nincs tudomásunk.

 

A kutatás célja, a megválaszolandó kérdések

Elsőként azt a problémát vizsgáltam, amikor egy nagy NA-jú fókuszáló rendszert fázismaszkkal modulált lézernyalábbal megvilágítva, adott intenzitásprofilú foltot szeretnénk létrehozni a fókuszsíkban. Egy lehetséges módszer erre a paraxiális esetben jól bevált Gerchberg–Saxton-féle iteratív Fourier-transzformációs algoritmus [13] vektori esetre történő általánosítása. Az irodalomban ismert ennek egy, lineáris polarizációjú megvilágításra kidolgozott esete [7]. A módszer olyan általánosítását tűztem ki célul, mely tetszőleges polarizációjú megvilágítás esetén alkalmazható.

 

Kutatásom második részében olyan vektori bázisfüggvények megalkotására törekedtem, melyek szemléletes fizikai jelentéssel bírnak és jól hasznosíthatóak inverz feladatok megoldásában. Elvárás, hogy megvalósuló fókuszmezőket reprezentáljanak (megoldásai legyenek a vektoriális Helmholtz-egyenletnek [14]) és  hordozzák a fókuszált nyalábokra jellemző irányítottságot, mely a korlátozott – a Θ félnyílásszögű kúp által meghatározott – térszögből érkező megvilágítás eredménye. Ezen felül azt a követelményt támasztottam, hogy numerikusan gyorsan és viszonylag egyszerűen számolhatóak legyenek, és segítségükkel egyszerűen kiterjeszthetővé váljon a fókuszfolt optimalizációja a háromdimenziós fókusztérfogatra is.

 

Módszerek és új eredmények

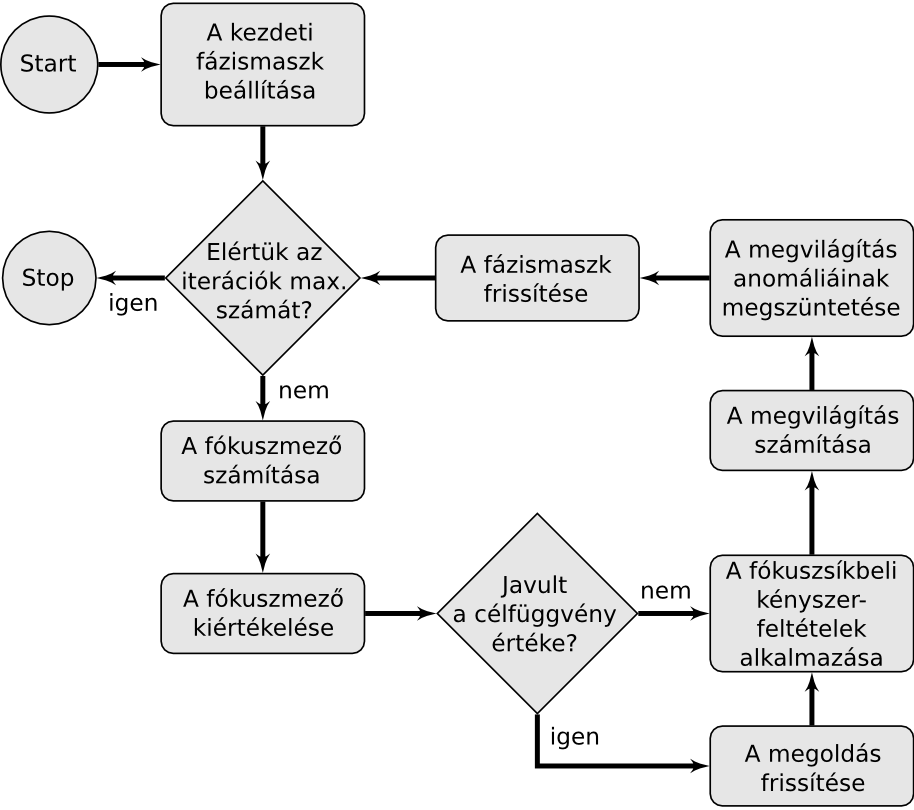
Az iteratív Fourier-transzformációs algoritmus vektori általánosítása a Debye–Wolf-elméleten [4, 5] alapul.  Az eljárás folyamatábráját a 3. ábra mutatja. A felvázolt ciklust ismételve a módszer egy, az előírt feltételeket közelítő megoldáshoz konvergál és megadja az azt létrehozó fázismaszkot.

 

A módszert a fókuszsíkban előírt, ún. flat-top (adott tartományon belül homogén, azon kívül zérus) intenzitáseloszlások esetére teszteltem. Célfüggvénynek a megvalósuló fókuszmező és az előírt intenzitás (flat-top-tartományra kiintegrált) négyzetes eltérését választottam. A flat-top-tartományon belül az intenzitás homogenizálása nemfizikai effektusokat eredményez a visszaszámolt megvilágításban, úgy mint nemtranszverzális polarizációs komponens ill. a belépő pupillán kívüli tartományban nemzérus térerősség megjelenése. Ezeket az anomáliákat szüntettem meg a fázismaszk frissítése előtt. Megoldásnak azt a fázismaszkot tekintettem, amelyre a célfüggvény értéke minimális volt. Jabbour és Kuebler [7] eljárásával összehasonlítva az új módszer mintegy 11-22%-kal nagyobb diffrakciós hatásfokot eredményező fázismaszkokat hozott létre [J1].

 

A második kutatási téma, az inverz probléma szempontjából előnyös, új fókuszmező-reprezentáció két távoli kutatási terület házasságából született: a jelfeldolgozásban és geofizikában ismert ún. koncentrálási problémát [15] oldottam meg a fókuszálás multipólelméletének sarokkövét képező vektor-multipólmezők [16] esetére.

 

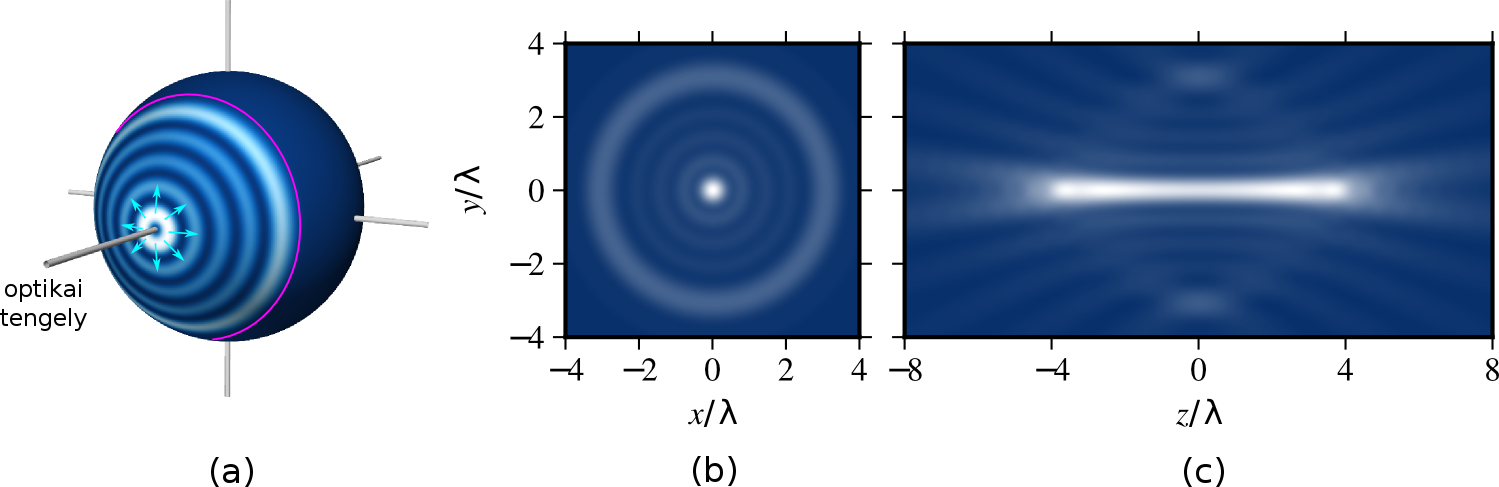
A koncentrálási probléma, melynek úttörő kutatói D. Slepian és kollégái voltak [17-20], olyan sávkorlátozott függvény keresését jelenti, amelynek energiája a lehető legnagyobb mértékben egy megadott, véges idő-/tértartományra korlátozódik. Jelen esetben ezt a problémát a vektor-multipólmezők síkhullámspektrumát reprezentáló vektor-gömbharmonikusok [16] esetére fogalmaztam meg, melynek eredményeképpen jó közelítéssel csupán a Θ félnyílásszögű gömbsapkára korlátozódó vektorfüggvényeket (a Slepian-féle vektor-gömbharmonikusokat) kaptam. Ezek újfajta, irányított jelleggel bíró fókuszmezőket (a Slepian-féle vektor-multipólmezőket) határoznak meg [J2]. A 4. ábra egy ilyen koncentrált Slepian-féle vektor-gömbharmonikus, valamint a hozzá tartozó Slepian-féle vektor-multipólmező intenzitáseloszlását mutatja.

 

 

Az új Slepian-féle bázisfüggvények segítségével a nagy NA-jú fókuszálás inverz problémája két fő lépésre válik szét: elsőként véges számú Slepian-féle vektor-multipólmező szuperpozíciójaként olyan fókuszmezőt alkotunk, mely optimálisan teljesíti az előírt fókusztérfogatbeli feltételt (például legkisebb négyzetek értelmében közelít egy előírt intenzitáseloszlást). Ez az esetek többségében egy nemlineáris optimalizációs probléma megoldását jelenti, amelyre az irodalomban fellelhető algoritmusok alkalmazhatóak és az eredménye  az optimális fókuszmező lineárkombinációjának együtthatói. A második lépésben ezek segítségével kombinálva a megfelelő Slepian-féle vektor-gömbharmonikusokat a fókuszmező vektori síkhullám-szögspektrumát kapjuk, amelyből a megvilágítás egyszerűen előállítható [J3].

 

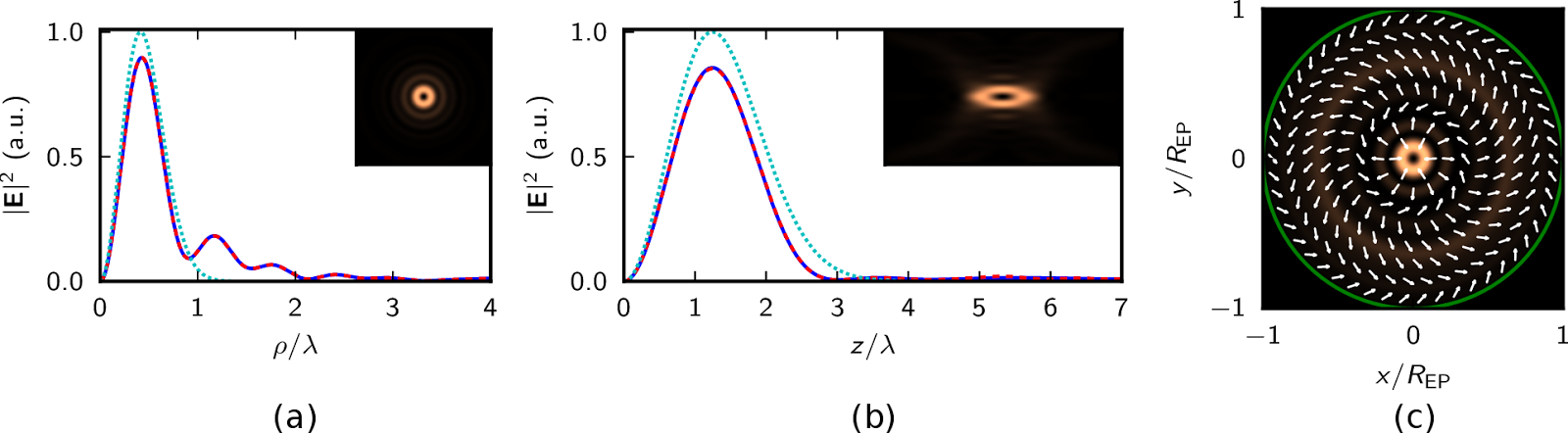
Az előbb leírt folyamat gyakorlati alkalmazhatóságát három nevezetes, fókusztérfogatbeli intenzitáseloszlás (az ún. optikai tű [11], optikai cső [12] és optikai buborék [21]) esetén keresztül demonstráltam [J3]. A buborékkal kapcsolatos eredményeket az 5. ábra mutatja.

 

 

 

A koncentrálási problémák általános jellemzője, hogy egy integráloperátor (az ún. koncentrálási operátor) rosszul kondicionált sajátérték-problémájának megoldására vezetnek [22]. Ez a Slepian-féle vektor-gömbharmonikusok előállításakor sincs másképp, és komoly numerikus instabilitást okozhat. Bizonyos skalár koncentrálási problémák esetén azonban létezik egy, a koncentrálási operátorral kommutáló Sturm–Liouville-féle [23] differenciáloperátor, melynek a sajátérték-problémája könnyen megoldható, így a numerikus instabilitások kiküszöbölhetőek [15]. Ilyen differenciáloperátor azonban a gömbsapkára korlátozott vektor-gömbharmonikusok koncentrálási problémája esetében – mely a Slepian-féle vektor-gömbharmonikusok esetében is felbukkan – ezidáig nem volt ismert.

 

Sikerült a szóban forgó koncentrálási problémát egy skalár problémára visszavezetnem és erre az esetre megtalálni a megfelelő, jól viselkedő, a probléma koncentrálási operátorával kommutáló  differenciáloperátort [J4]. Ezzel a Slepian-féle vektor-gömbharmonikusok kiszámítására numerikusan stabil és gyors algoritmust adtam.

 

Várható impakt, további kutatás

A doktori munkám során megjelent cikkeimre [J1-J4] az írás pillanatáig 14 független hivatkozás érkezett, az iteratív Fourier-transzformációs algoritmus vektori adaptációjára egy Progress in Optics fejezet is hivatkozik [25]. Eredményeimet két nemzetközi konferencián mutattam be [J5, J6].

 

A Slepian-féle vektor-gömbharmonikusok nem csupán az optikában, hanem a geofizikában is nagyon jól hasznosíthatóak [24]. Mivel ezeknek a numerikusan stabil előállítása kiemelten fontos kérdés, a kommutáló differenciáloperátorral kapcsolatos eredményeimre hivatkozik a közeljövőben megjelenő Handbook of Geomathematics [26] második kiadása is.

 

A felvázolt módszerek továbbfejlesztésére számos lehetőség kínálkozik. Érdemes lenne megvizsgálni a vektoriális iteratív Fourier-transzformációs módszer kiterjesztését háromdimenziós (fókusztérfogatban előírt) kényszerek esetére. Erre a skalár esetben már van az irodalomban példa [27, 28].

 

A Slepian-féle vektorfüggvények kapcsán is számos kutatási irány felmerül: egyrészt a jelenleginél hatékonyabb optimalizációs módszereket lehetne keresni az előírt fókusztérfogatbeli intenzitáseloszlás Slepian-féle vektor-multipólmezőkkel történő approximációjára, másrészt fejleszteni lehetne a kiértékelésükkel kapcsolatos numerikus módszereket, ami gyorsabb optimalizációt eredményezne. Az irodalomban fellelhető egyéb módszerekkel [10, 11] történő összehasonlítás is tanulságos lenne.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája

 

[J1] K. Jahn and N. Bokor. Intensity control of the focal spot by vectorial beam shaping. Opt. Commun., 283(24):4859–4865, 2010.

 

 

[J2]  K. Jahn and N. Bokor. Vector Slepian basis functions with optimal energy concentration in high numerical aperture focusing. Opt. Commun., 285(8):2028–2038, 2012.

 

[J3] K. Jahn and N. Bokor. Solving the inverse problem of high numerical aperture focusing using vector Slepian harmonics and vector Slepian multipole fields. Opt. Commun., 288:13–16, 2013.

 

[J4] K. Jahn and N. Bokor. Revisiting the Concentration Problem of Vector Fields within a Spherical Cap: A Commuting Differential Operator Solution. J. Fourier Anal. Appl., 20(2):421–451, 2014.

 

[J5] K. Jahn and N. Bokor: Using a vector Slepian basis in high numerical aperture focusing. Konferenciaposzter. Focus on Microscopy 2011, Konstanz.

 

[J6] K. Jahn and N. Bokor. Vector Slepian functions and the inverse problem of high numerical aperture focusing. Proc. SPIE, 8550:855038, 2012.

 

Linkgyűjtemény

 

Mikroszkópiával kapcsolatos információk:

Olympus Microscopy Resource Center

Nikon Microscopyu

 

Kutatók és kutatócsoportok honlapjai:

Emil Wolf honlapja

Török Péter kutatócsoportja

Colin Sheppard kutatócsoportja

Stefan Hell kutatócsoportja

Nir Davidson kutatócsoportja

Frederik Simons kutatócsoportja

The Institute of Optics, University of Rochester

Two-Photon Imaging Center (Budapest)

 

Hivatkozások listája

 

[1] P. Török and F.-J. Kao. Optical Imaging and Microscopy: Techniques and Advanced Systems. Springer, Berlin, second edition, 2007.

 

[2] A. Ashkin. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA, 94:4853–4860, 1997.

 

[3] T. Itani, W. Wakamiya, J. Cashmore, and M. Gower. 157-nm lithography with high numerical aperture lens for sub-70 nm node. Microelectron. Eng., 67:39–46, 2003.

 

[4] E. Wolf. Electromagnetic diffraction in optical systems. I. An integral representation of the image field. Proc. R. Soc. London Ser. A, 253 (1274):349–357, 1959.

 

[5] B. Richards and E. Wolf. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc. R. Soc. London Ser. A, 253(1274):358–379, 1959.

 

[6] C. J. R. Sheppard and P. Török. Efficient calculation of electromagnetic diffraction in optical systems using a multipole expansion. J. Mod. Opt., 44(4):803–818, 1997.

 

[7] T. G. Jabbour and S. M. Kuebler. Vectorial beam shaping. Opt. Express, 16(10):7203–7213, 2008.

 

[8] R. Kant. Superresolution and increased depth of focus: an inverse problem of vector diffraction. J. Mod. Opt., 47(5):905–916, 2000.

 

[9] M. R. Foreman, S. S. Sherif, P. R. T. Munro, and P. Török. Inversion of the Debye–Wolf diffraction integral using an eigenfunction representation of the electric fields in the focal region. Opt. Express, 16(7):4901–4917, 2008.

 

[10] J. J. M. Braat, P. Dirksen, A. J. E. M. Janssen, S. van Haver, and A. S. van de Nes. Extended Nijboer–Zernike approach to aberration and birefringence retrieval in a high-numerical-aperture optical system. J. Opt. Soc. Am. A, 22(12):2635–2650, 2005.

 

[11] J. Wang, W. Chen, and Q. Zhan. Engineering of high purity ultra-long optical needle field through reversing the electric dipole array radiation. Opt. Express, 18(21):21965–21972, 2010.

 

[12] J. Wang, W. Chen, and Q. Zhan. Three-dimensional focus engineering using dipole array radiation pattern. Opt. Commun., 284(12):2668–2671, 2011.

 

[13] R. W. Gerchberg and W. O. Saxton. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik (Jena) 35:237, 1972.

 

[14] J. D. Jackson. Classical Electrodynamics. Wiley, Hoboken, NJ, third edition, 1999.

 

[15] F. J. Simons, . A. Dahlen, F, and M. A. Wieczorek. Spatiospectral concentration on a sphere. SIAM Rev., 48(3):504–536, 2006.

 

[16] N. J. Moore and M. A. Alonso. Closed-form bases for the description of monochromatic, strongly focused, electromagnetic fields. J. Opt. Soc. Am. A, 26(10):2211–2218, 2009.

 

[17] D. Slepian and H. O. Pollak. Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty–I. Bell Syst. Tech. J., 40(1):43–63, 1961.

 

[18] H. J. Landau and H. O. Pollak. Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty–II. Bell Syst. Tech. J., 40(1):65–84, 1961.

 

[19] H. J. Landau and H. O. Pollak. Prolate Spheroidal Wave Functions,Fourier Analysis and Uncertainty–III: The Dimension of the Space of Essentially Time- and Band-limited Signals. Bell Syst. Tech. J., 41(4):1295–1336, 1962.

 

[20] D. Slepian. Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty–IV: Extensions to Many Dimensions; Generalized Prolate Spheroidal Functions. Bell Syst. Tech. J., 43(6):3009–3057, 1964.

 

[21]  N. Bokor and N. Davidson. A three dimensional dark focal spot uniformly surrounded by light. Opt. Commun., 279(2):229–234, 2007.

 

[22] B. Bell, D. B. Percival, and A. T. Walden. Calculating Thomson’s spectral multitapers by inverse iteration. J. Comput. Graph. Stat., 2(1):119–130, 1993.

 

[23] G. B. Arfken, H. J. Weber, and F. E. Harris. Mathematical Methods for Physicists: A Comprehensive Guide. Academic Press/Elsevier, Waltham, MA, 7th edition, 2012.

 

[24] A. Plattner and F. J. Simons. Spatiospectral concentration of vector fields on a sphere. Appl. Comput. Harmon. Anal., 36(1):1–22, 2014.

 

[25] Z. Chen, H. Limin and P. Jixiong. Tight Focusing of Light Beams: Effect of Polarization, Phase, and Coherence. In Progress in Optics 57:219-259, 2012.

 

[26] A. Plattner and F. J. Simons. Potential-field estimation using scalar and vector Slepian functions at satellite altitude. In W. Freeden, M. Z. Nashed, and T. Sonar, editors, Handbook of Geomathematics. Springer, Berlin, second edition. to appear.

 

[27] G. Shabtay. Three-dimensional beam forming and Ewald’s surfaces. Opt. Commun., 226(1):33–37, 2003.

 

[28] G. Whyte and J. Courtial. Experimental demonstration of holographic three-dimensional light shaping using a Gerchberg–Saxton algorithm. New J. Phys., 7(1):117, 2005.

 

[F1] Forrás: http://www.sciencephoto.com/media/112553/enlarge