|
|
BMe Kutatói pályázat |
|
Fizikai Tudományok Doktori Iskola
BME TTK, Fizika Tanszék/Fizikai Intézet
Témavezető: Dr. Csonka Szabolcs
Cooper-pár feltörő nanoáramkör továbbfejlesztése
A kutatási téma néhány soros bemutatása
Kutatómunkám során összetett, szupravezető és normál fázisú vezetőt is tartalmazó nanoáramkörben fellépő kvantumjelenségeket vizsgálok elektromos transzportméréseken keresztül. A kutatás célja olyan összefonódott elektronpárokat szolgáltató nanoeszköz kifejlesztése, amely lehetővé teszi kvantumösszefonódás kísérleti vizsgálatát szilárdtest környezetben, és kvantumszámítógép részeként képes összefonódott kvantumbiteket előállítani.
A kutatóhely rövid bemutatása
A méréseket Dr. Csonka Szabolcs kutatócsoportjában, a Fizika Tanszék Alacsony hőmérsékleti transzportlaboratóriumában végzem. A laboratórium egyedülálló lehetőséget biztosít alacsony hőmérsékleti mérések kivitelezésére a 4,2 K - 50 mK hőmérséklettartományban, lehetővé téve számos nanofizikai kutatás folytatását.
A kutatás széleskörű nemzetközi együttműködés keretében zajlik.
A kutatás történetének, tágabb kontextusának bemutatása
Az összefonódás egy mélyreható következményekkel járó kvantummechanikai jelenség [1], amely amellett, hogy alapfizikai jelentőséggel bír, a kvantumszámítógépek működési alapjául is szolgál. Két részecske összefonódott állapotban van, ha hullámfüggvényük nem írható fel egyrészecske hullámfüggvények szorzataként. Ilyen összefonódott foton-párokkal már végeztek kísérleteket, ezekben példát mutattak a Bell-egyenlőtlenség sérülésére. Szilárdtest környezetben azonban még nem végeztek hasonló kísérleteket; az ehhez szükséges eszköz, amely elegendően magas hatásfokkal képes térben szétvált, összefonódott elektronpárokat szolgáltatni [2], nem áll rendelkezésre.
Kvantumbitet, amiben a kvantumszámítógép az információt tárolja és amin a számításokat végzi, meg lehet valósítani tetszőleges kétállapotú kvantummechanikai rendszerrel, így például egy elektronspinnel [3]. A kvantumalgoritmusok a kvantumbitek összefonódottságát kihasználva képesek bizonyos számítási feladatokat a klasszikus társaiknál hatékonyabban megoldani. Chipbe integrált szilárdtest kvantumszámítógépben egy összefonódott elektronpárokat szolgáltató eszköz alkalmas lenne arra, hogy a kvantumbiteket összefonódott állapotba inicializálja, így készítve azokat elő a kvantumalgoritmus számára.
A kutatás célja, a megválaszolandó kérdések.
Összefonódott elektronok természetes forrása egy szupravezető, amelynek alapállapotát spin-szinglet párokba rendeződött elektronpárok, ún. Cooper-párok alkotják. Ezeket az elektronokat alagúteffektus révén lehet a szupravezetőből kinyerni, térbeli szétválásukat a Coulomb-taszítást kihasználva érhetjük el. A közelmúltban megvalósítottak olyan nanoáramköröket, amelyek ezen az elven képesek Cooper-párokat felhasítani, azonban ezek hatásfoka alacsony volt [4-5]. A kutatás célja a Cooper-pár feltörő nanoáramkörben fellépő jelenségek megértése és nagy hatásfokú, új generációs Cooper-pár feltörő nanoáramkör készítése, amely megnyitja a lehetőséget a felhasított elektronpárok összefonódottságának vizsgálatára.
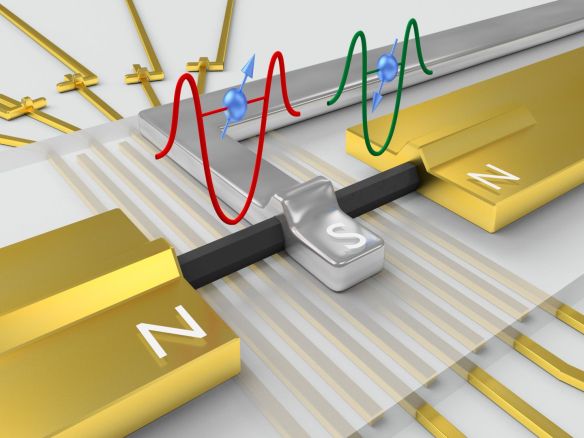
1. ábra Az újonnan megvalósított Cooper-pár feltörő látványképe. A hatszög keresztmetszetű, fekete színnel ábrázolt nanopálca egy szigetelőrétegen fekszik, középen egy szupravezető, két oldalt pedig normál elektródákkal kontaktálva. A szigetelőréteg alatti párhuzamos kapuelektródák sora teszi lehetővé, hogy hangoljuk a kémiai potenciált a nanopálcában, és így kvantumpöttyöket alakítsunk ki.
Módszerek
A Cooper-pár feltörő nanoáramkör egy szupravezetőből, két hozzá csatolt kvantumpöttyből és két normál elektródából áll (2. ábra). A kvantumpöttyök olyan izolált térrészek, amelyekben az elektronok diszkrét energianívókat töltenek be, ezek távolságát elsősorban a Coulomb-kölcsönhatás határozza meg. Az elektronok taszítása miatt az a transzportfolyamat, amiben egy Cooper-pár kilép a szupravezetőből és mindkét elektronja ugyanazt a kvantumpöttyöt tölti be, energetikailag kedvezőtlen, ez kényszeríti ki a térbeli szétválásukat. A Cooper-pár feltörési folyamatban a pár két elektronja a két kvantumpöttyön keresztül, ellentétes irányban távozik a normál elektródák felé. Emellett azonban jelen vannak parazita folyamatok is, amik a hatásfokot csökkentik, pl. egy elektronpár szekvenciális alagutazása ugyanazon kvantumpöttyön keresztül.
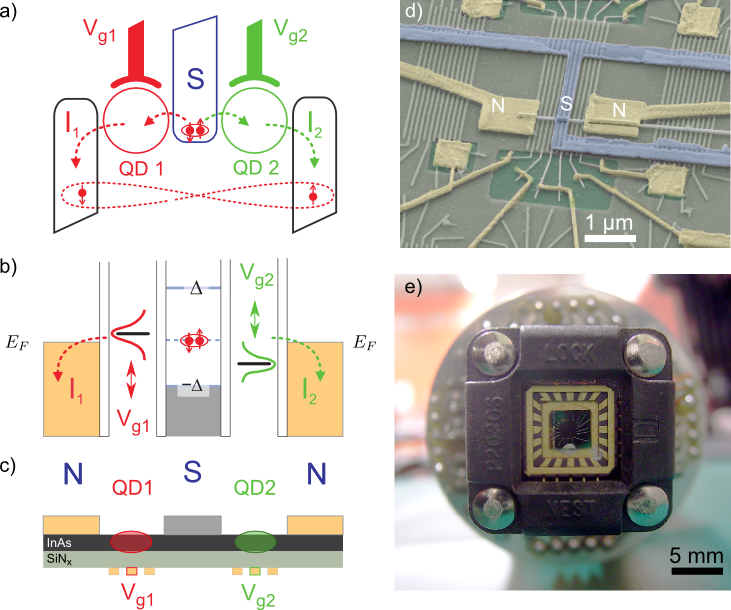
2. ábra a) A Cooper-pár feltörő sematikus rajza. [5] b) Az eszköz energiadiagramja egyensúlyi állapotban. A normál elektródák Fermi-energiája egybeesik a Cooper-párok energiájával, az elektródákban EF alatt, illetve a szupravezető tiltott sáv alatt az összes állapot betöltött. A kvantumpöttyök nívóit a Vg1 és Vg2 kapufeszültségekkel hangoljuk. c) A nanoszerkezet egyszerűsített keresztmetszeti rajza. A kvantumpöttyöket az indium-arzenid (InAs) nanoszálban alakítjuk ki, az elektronokat bezáró potenciálgátat a vékony szigetelőréteg alatti kapuelektródákra kapcsolt feszültséggel hozzuk létre, ugyanezekkel hangoljuk a kvantumpöttyök nívóit. d) Pásztázó elektronmikroszkópos felvétel egy Cooper-pár feltörőről (színezve) [S2]. e) A szilícium hordozó chiptartóba ragasztva.
Mintakészítés
A Cooper-pár feltörő áramköröket elektronsugaras litográfiával készítjük, a módszer lépéseit a 3. ábra szemlélteti. A szilícium hordozót lakkréteggel borítjuk be, amit pásztázó elektronmikroszkópban elektronokkal világítunk meg, ennek hatására a lakkban kémiai változás megy végbe, és a megvilágított részek az előhívó folyadékban oldhatóvá válnak. Előhívás után jutunk a megmintázott maszkhoz, amit az adott mintakészítési lépésben többféle eljárás követhet, nedves kémiai kezelés, száraz marás vagy fémréteg leválasztás vákuumgőzöléssel. Az új generációs Cooper-pár feltörő készítése négy litográfiás ciklust igényel: a vékony kapuelektródák sorának elkészítése után létrehozzuk az ezt fedő szilícium-nitrid szigetelőréteget, mikromanipulátorral ráhelyezzük az indium-arzenid nanopálcát, és a két hátralévő lépésben kontaktáljuk szupravezető (nióbium) és normál (titán/arany) elektródákkal.
3. ábra Az elektronsugaras litográfia lépései (sorozatkép)
Méréstechnika
Az elkészült nanoáramköröket 3He-4He rendszerű kriosztátban, ~50 mK hőmérsékleten karakterizáljuk. A kis jelszintű, alacsony hőmérsékleti mérések számos nehézséggel járnak, az elektromos vezetékeket megfelelő szűréssel látjuk el, a nanoáramkörben folyó kis áramokat lock-in technikával mérjük. A kontrollkísérlethez szükséges mágneses teret a kriosztátba épített szupravezető vektormágnes biztosítja, ami képes egy síkban tetszőleges irányba mutató mágneses teret előállítani 3 tesláig, így lehetővé teszi anizotrópia vizsgálatát is. A műszerek GPIB buszon és Ethernet felületen keresztül csatlakoznak a számítógéphez, amin a mérésvezérlő program fut, ez irányítja a műszereket és valós időben ábrázolja a mérési adatokat.
Eddigi eredmények
Az alapjelenség
A 4. ábra mutatja be az alapjelenség mérésének menetét. Miután a kapuelektródákra kapcsolt feszültséggel kialakítottuk a potenciálgátakat és kvantumpöttyöket formáltunk, a jobb oldali kvantumpöttyöt rezonanciára hangoljuk. Amíg a bal oldali kvantumpöttynek nincs egy nívója sem az EF Fermi-energiánál, ebben az ágban első rendben nem folyik áram, a pötty Coulomb-blokádban van. Ahogy ennek a pöttynek a nívóit hangoljuk, és azok áthaladnak a Fermi-energián, a Coulomb-blokád feloldódik, a pöttyön véges áram folyik. Ezzel egyidőben egy-egy rezonanciánál megnő a jobb oldali pöttyön átfolyó áram is, ez a Cooper-pár feltörés jele: mindkét oldal egyidejű rezonanciájánál válik kedvezővé a feltörési folyamat. Ha mágneses térrel elnyomjuk a szupravezetést, a pozitív járulék ebben az ágban eltűnik (szaggatott görbe).
4. ábra A Cooper-pár feltörés kísérleti kimutatása. A grafikonon a piros görbe a bal oldali kvantumpötty vezetőképességét mutatja (skála bal oldalt), a zöld görbe a jobbét (skála jobb oldalt). A bal oldali pötty rezonanciái a jobb oldali pöttyben is pozitív járulékként mutatkoznak meg, ez a Cooper-pár feltörés jellegzetessége.
Az első Cooper-pár feltörő áramkörök nem rendelkeztek kapuelektróda-sorral, ezért számos paraméterük esetleges volt és nem lehetett őket megváltoztatni. Az elkészült új generációs áramkörökben a kapuelektródák lehetővé teszik több paraméter (kvantumpötty-elektróda csatolások) in-situ hangolását, ezzel a korábbi
![]() -vel definiált hatásfokot néhány százalékról 30% fölé sikerült növelni.
-vel definiált hatásfokot néhány százalékról 30% fölé sikerült növelni.
Várható impakt, további kutatás
Eddigi eredményeinket magas impaktú vezető folyóiratban közöltük [S1], illetve a tudományterületen dolgozókkal poszter prezentáció formájában osztottuk meg [S2]. A legújabb mérési eredményeket összefoglaló publikáció jelenleg előkészítés alatt van.
A kutatást egyfelől a nanoszerkezet további fejlesztésének irányába folytatjuk: más szupravezető elektródával (pl. vanádium, volfrám-rénium, ólom) készítünk áramköröket, illetve hosszú távon új mérési módszerekkel olyan kísérleteket végzünk, amellyel a felhasított Cooper-párok spin karakterét és összefonódottságát vizsgálhatjuk.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
[S1] L. Hofstetter, S. Csonka, A. Baumgartner, G. Fülöp, S. d’Hollosy, J. Nygård, and C. Schönenberger, Finite-Bias Cooper Pair Splitting, Phys. Rev. Lett. 107, 13680, 2011
[S2] S. d’Hollosy , G. Fülöp, A. Baumgartner, S. Csonka, M.H. Madsen, J. Nygård and C. Schönenberger, Electrical tunability of InAs nanowire quantum dots and Cooper pair splitting, poster presentation, Frontiers in Quantum Engineered Devices, 2013
[S3] Róbert Erdélyi, Morten Hannibal Madsen, György Sáfrán, Zoltán Hajnal, István Endre Lukács, Gergő Fülöp, Szabolcs Csonka, Jesper Nygård, János Volk, In-situ mechanical characterization of wurtzite InAs nanowires, Solid State Communications, 10/2012; 152(19):1829–1833
Linkgyűjtemény
Kapcsolódó szócikkek a Fizipédiáról:
Kapcsolódó szócikkek a Wikipédiáról:
- Kvantumösszefonódás
- Bell-teszt (angolul)
Hivatkozások listája
[1] A. Einstein, B. Podolsky, and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Phys. Rev. 47, 777
[2] Waldemar Kłobus, Andrzej Grudka, Andreas Baumgartner, Damian Tomaszewski, Christian Schönenberger, and Jan Martinek, Entanglement witnessing and quantum cryptography with non-ideal ferromagnetic detectors, Phys. Rev. B 89, 125404 (2014)
[3] J. R. Petta et al. Coherent Manipulation of Coupled Electron Spins in Semiconductor Quantum Dots. Science, 309:2180–2184 (2005)
[4] L. G. Herrmann et al. Carbon nanotubes as Cooper-pair beam splitters. Phys. Rev. Lett., 104(2):026801 (2010)
[5] L. Hofstetter, S. Csonka, J. Nygard, and C. Schonenberger. Cooper pair splitter realized in a two-quantum-dot Y-junction. Nature, 461:960–963 (2009)
