 |
BMe Kutatói pályázat |

|
BME Villamosmérnöki Tudományok Doktori Iskola
BME VIK, Távközlési és Médiainformatikai Tanszék
Témavezető: Dr. Cinkler Tibor, Dr. Várallyay Zoltán
Optikai távközlő rendszerek nemlineáris eszközeinek matematikai modellezése és kísérleti vizsgálata
A kutatási téma néhány soros bemutatása
Kutatásom napjaink és a jövő optikai hálózataiban potenciálisan kihasználható, kétféle nemlineáris optikai jelenségeken alapuló eszköz vizsgálatára terjed ki: ezek a telítődő abszorbensek és a periodikusan polarizált lítium-niobát (PPLN) hullámvezetők. A kutatás magában foglalja ezen eszközök fényforrásokban és jelregenerátorként való hálózati implementálhatóságának feltárását, valamint a bennük lezajló fizikai folyamatok kísérleti úton, számításokkal, matematikai modell alkotással és számítógépes szimuláció útján történő megértését.
A kutatóhely rövid bemutatása
Kutatásaimat a Távközlési és Médiainformatikai Tanszéken végzem, szoros kapcsolatban hazai és külföldi partnerekkel. Csoportunk elsősorban matematikai modellezésre és számítógépes szimulációra koncentrál, de a Furukawa Electric Technológiai Intézet Kft. és külföldi partnerintézményei segítségével jelentős kísérleti munkát is végzünk. A japán National Institute of Information and Communications Technology-val együttműködve a rendszeresen odalátogató vendégkutatóink az ottani, kiemelkedően magas színvonalú Photonic Network System Laboratory-ban dolgoznak a témához kapcsolódó kísérleteken.
A kutatás történetének, tágabb kontextusának bemutatása
A kutatás két fő területet ölel fel. Az egyik a telekommunikációban [1] is alkalmazott, optikai szál alapú lézerek (szállézerek) számítógépes modellezése és a bennük fellépő fizikai hatások vizsgálata. A szállézerek jelentősége, hogy olyan hullámhosszakon képesek jó minőségű nyalábok létrehozására (erbium, itterbium, neodímium szállézerek), ahol a szilárdtest lézerek gyengébb tulajdonságokat mutatnak.
1. ábra: a) Erbium adalékolású, ultrarövid impulzusú szállézer laboratóriumi megvalósítása; b) széles spektrumú, kommerciális szállézer (bővebben: a képekre kattintva)
A napjainkban kutatott ultrarövid (10-12 – 10-15s) impulzusú szállézerek módusszinkronizációja (az ultrarövid impulzusok keltéséhez szükséges fizikai folyamat) elsősorban passzív nemlineáris (a fényintenzitásra változó fizikai paraméterű) eszközökkel, telítődő abszorbensekkel [2] történik. Ez más módusszinkronizálási módszerekkel összevetve rövidebb impulzusokat és egyszerűbb, stabilabb felépítést eredményez. A telítődő abszorbens alapú szállézerek számos kísérleti vizsgálat tárgyát képezik, emellett azonban az elméleti és szimulációs munkák szerepe is fontos a lézerben zajló folyamatok együttes hatásának megértése és a lézer fontos paramétereinek előrejelzése szempontjából [3].
A fellépő nemlineáris optikai jelenségek nemcsak impulzus üzemű lézerek esetén fontosak, hanem folytonos üzemben is, ahol megváltoztathatják a nyaláb paramétereit és spektrumát [4].
A másik fő terület az alapvető fizikai folyamatok tekintetében rokon, alkalmazás szempontjából azonban eltér. Ez a zajjal terhelt optikai jelek tisztán optikai regenerálásának megvalósítása [5], továbbá a jelenleg alkalmazottnál alacsonyabb (ún. ultra alacsony) zajú optikai erősítés [6] elméleti és kísérleti vizsgálata, különösképpen a nagy gyakorlati jelentőséggel bíró hullámhosszosztásos rendszerekben.
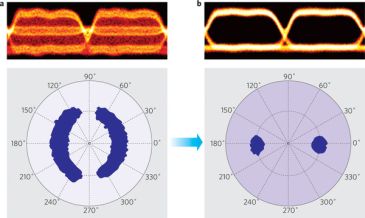
2. ábra: Fázis- és amplitúdózajjal terhelt jel és regenerált formája a komplex számsíkon [5]
A jelenlegi optikai adatátviteli rendszerekben a fázismodulált jelek regenerálását az elektromos tartományban valósítják meg [7] az optikai jeleket elektromos jellé konvertálva, majd visszaalakítva az optikai tartományba. A tisztán optikai fázisregenerálás kizárólag az optikai tartományban történik, amely egyszerűbb, olcsóbb és gyorsabb megoldást jelent. A regeneráláshoz PPLN kristályt alkalmazunk, ami számos előnyös tulajdonsággal bír a hálózati implementáció szempontjából [C1], és eddigi eredményeink szerint [C1, C2] a hullámhosszosztásos rendszerek alacsony zajú és áthallású erősítésében is ígéretes.
A kutatás célja, a megválaszolandó kérdések
Ultrarövid impulzusú lézerek esetében a telítődő abszorbens paramétereinek lézerműködésére gyakorolt hatását a saját matematikai modellünkkel és annak számítógépes szimulációjával vizsgálom [J1]. A vizsgálat lényege, hogy a részletes matematikai tárgyalás segítségével lehetővé tegye olyan paraméterek és jelenségek kölcsönhatásának megértését – elsősorban a telítődő abszorbens paramétereinek és a lézer polarizációs stabilitásának kapcsolatát –, amelyek az irodalomban korábban nem voltak fellelhetők. Ezen túlmenően célom feltárni a különböző impulzusparaméterek létrehozásához szükséges telítődő abszorbens beállításokat, amelyek meghatározása kísérleti elemzéssel nehézkes volna.
A folytonos üzemű, nagy teljesítményű (több száz wattos) szállézerek vizsgálatakor a cél, hogy a modell segítségével elősegítsem a szállézerben zajló nemlineáris optikai folyamatok és a spektrális szélesség között fennálló kapcsolat megértését. Minden esetben lehetőségünk volt a felállított modellek kísérleti ellenőrzésére, amire fokozott figyelmet fordítottunk.
A PPLN kristály jelregenerálási tulajdonságainak vizsgálatakor kísérleteken keresztül mutatom be, hogy a tisztán optikai fázisregenerálás megvalósítható PPLN felhasználásával, kihasználva a kristályban fellépő másodrendű nemlinearitásokat.
Ezek a – fázisregenerálás szempontjából szintén kutatott – nemlineáris optikai szálakban fellépő folyamatokkal [5] analóg módon hatnak a fázismodulált jelekre, és megfelelő beállítások mellett csökkentik a fáziszajt.
Matematikai modellünk és további kísérletek segítségével végül a PPLN-ben megvalósítható többcsatornás, alacsony zajú erősítés lehetőségét vizsgálom. Célom annak bemutatása, hogy PPLN kristályban lehetséges több csatorna egyidejű erősítése, a nemlineáris szálhoz képest alacsonyabb áthallás mellett. Ezen tulajdonság a hullámhosszosztásos rendszerek jelenleginél kevesebb zajjal járó erősítését tenné lehetővé [6].
Módszerek
A szállézerek modellezésekor elsődleges szempont volt, hogy a felállított modell egyszerre írja le az szálakban fellépő nemlineáris hatásokat és a lézerműködés egyenleteit, beleértve az energiaszintek betöltöttségét a lézer oszcillátor egyes pozícióiban, mindkét merőleges polarizációs komponenst figyelembe véve.
Ezzel a tárgyalással a lézerek működéséről az irodalomban fellelhető modellek nagy részénél pontosabb leírás adható. Továbbá absztrakt modell paraméterek helyett olyan jellemzők beállítását teszi lehetővé - úgymint abszorpciós és emissziós hatáskeresztmetszetek, az erősítőközeg adalékolásának koncentrációja, a szálak magátmérője, stb. -, amelyek közvetlenül átültethetők a mérési összeállításokba, megkönnyítve ezzel a kísérleti és elméleti munkák összehangolását.
A fenti modell impulzus és folytonos üzemű lézerek esetében egyaránt alkalmazható. Az impulzus üzemű lézer modelljének vázlata a 3. ábrán látható.
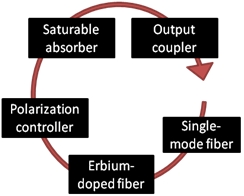
3. ábra: Az impulzus üzemű szállézer modelljének vázlata
Az impulzus üzemű lézerek stacioner működése kiindulási zajból épül fel. A szálakban és a telítődő abszorbensben fellépő nemlineáris hatások együttesen szinkronizálják a módusokat (azok spektrális amplitúdóját és fázisát), ultrarövid impulzusokat létrehozva.
Folytonos üzemű lézerek esetében komplikációt jelent a spektrum kiszélesedésének modellezése, hiszen a valóságos lézerek nem egyetlen diszkrét hullámhosszon sugároznak, hanem egy keskeny tartományon. Ezen jelenség figyelembe vétele elengedhetetlen a fellépő nemlinearitások vizsgálatához. A spektrum szélessége korábbi elméleti eredmények alapján a lézer időbeli fázisának sztochasztikus Wiener folyamat szerinti változásával jellemezhető [8].
A jelregenerálás kísérleti megvalósítása a fázisérzékeny erősítőn alapszik, amelynek elvi működése a 4. ábrán látható. A belépő signal és pump közti kölcsönhatást különböző másodrendű nemlinearitások együttesen biztosítják, amit kaszkádosított nemlinearitásnak nevezünk. A kaszkádosított nemlinearitások eredménye az első PPLN-ben felépülő ún. idler, amely fázisban korrelált a bemeneti signal-hoz és pump-hoz. Szintén kaszkádosított nemlinearitások eredménye a 2. PPLN-ben a fázisérzékeny erősítés. Az erősítő fáziszajjal rendelkező bináris fázismodulált (BPSK) jelek zajának csökkentésére képes (2. ábra), amely zajokat a “Phase manipulation” blokkban (4. ábra). adjuk hozzá a signal-hoz. Ezen zajkomponenseket a fázisuk alapján “ismeri fel” és gyengíti le az erősítő, felhasználva az idler-ben tárolt fázist, miközben az zajmentes signal komponenseket erősíti.

4. ábra: A fázisérzékeny erősítő és a fázisviszonyok
A PPLN segítségével megvalósítandó jelregenerátor ún. black-box típusú eszköz, azaz a modulációt képes törölni a bejövő jelről, és az így kapott vivőhullámot használja idler létrehozásához. Következésképp, nem szükséges egy előre generált idler. Az így kapott idler-rel a bejövő signal fázisérzékenyen erősíthető, és így a fáziszaja eltüntethető. Összehasonlításként, a 4. ábrán bemutatott erősítő csak egy már meglévő vivőhullám és létrehozott idler után modulált jelet tud regenerálni.
A fázisérzékeny erősítő elve alkalmazható a hullámhosszosztásos rendszerek esetében az alacsony zajú fázisérzékeny erősítés leírására. A vizsgálatot néhány esetben kísérletileg végeztük el, majd egy általános modellt készítettünk, ami minden hullámhosszú csatorna kölcsönhatását figyelembe veszi, és a kaszkádosított nemlinearitások csatolt differenciálegyenleteit oldja meg. Segítségével a hullámhosszak közötti parazita áthallás számítható tetszőleges számú, egymás után kapcsolt erősítőre.
Eddigi eredmények
A fentebb említett célok túlnyomó része az írás időpontjára megvalósult. Ezek az alábbiak:
A szállézerek vizsgálatakor egy speciális, távközlési célokra használt oszcillátorban sikerült kimutatnom a telítődő abszorbens paramétereinek és a lézer stabilitásának kapcsolatát [J1]. A stabilitás a legtöbb alkalmazás szempontjából kritikus paraméter. Meghatároztam azokat az abszorbens beállításokat, amelyek mellett a lézer működése a mechanikai hatásokra érzéketlen marad. Az 5. ábrán az impulzusok energiáját és félérték szélességét ábrázoltam egy ilyen stabil beállítás mellett, egy másik abszorbens paraméter függvényében. Látható, hogy a polarizáció széles tartományában (különböző görbék) ezek a mennyiségek változatlanok, azaz a lézer mechanikailag stabil.
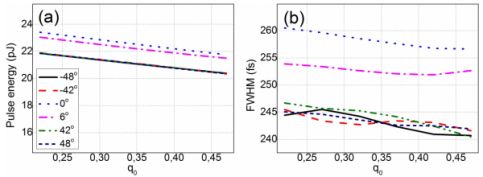
5. ábra: Impulzus energia és szélesség, mechanikailag stabil paraméter beállítások mellett
Folytonos üzemű lézerek esetében mérésekkel sikerült igazolni a felállított modell érvényességét, amely megmutatja a szál nemlinearitásának és a spektrális szélességnek a kapcsolatát. Az ide tartozó publikáció jelenleg bírálat alatt van. [J2]
A jelregenerálás témakörén belül kísérletileg megvalósítottam az első PPLN-alapú, tisztán optikai, black-box típusú fázisregenerátort [J3]. Ez az első olyan black-box regenerátor, amelyben mind az idler létrehozása, mind a fázisérzékeny erősítés PPLN segítségével történik. A 6. ábra a fázisérzékeny erősítő különböző beállításai esetén mutatja a regenerálás hatékonyságát az összeállítással.

6. ábra: A regenerálás hatékonysága különböző erősítő beállítások mellett
Kísérletileg megmutattuk, hogy a PPLN fázisérzékeny erősítőt egyszerre több csatornára alkalmazva a csatornák közti áthallás alacsonyabb, mint nemlineáris szál alapú erősítőkben. Az eredmény a PPLN potenciális használhatóságát mutatja többhullámhosszas rendszerek fázisérzékeny erősítésében [C1,C2].
Ezen eredményt arra is felhasználtuk, hogy az erősítő modelljét ellenőrizzük, és a belőle kapott számítással összehasonlítottuk a PPLN és a nemlineáris szál alapú erősítők áthallását összetettebb rendszerek - úgymint magasabb csatornaszám, több erősítő fokozat - esetében, amelyek kísérletileg egyelőre nehézkesen vizsgálhatók. Az eredményeket összefoglaló publikáció [J4] jelenleg elbírálás alatt van.
Várható impakt, további kutatás
Az eredményekhez szorosan kapcsolódó publikációk közül két folyóirat cikk és két konferencia cikk már megjelent; lazábban kapcsolódik ide további egy megjelent folyóirat és két konferencia cikk. Egy további publikációt folyóiratban mostanra elfogadtak, két másik pedig bírálat alatt van. A megjelenések helyei szinte kivétel nélkül a legszínvonalasabb száloptikai folyóiratok és fórumok.
A folytatás legvalószínűbb iránya az alacsony zajú fázisérzékeny erősítés kísérleti vizsgálata több csatornára és több erősítő fokozatra, hiszen ez a lépés elengedhetetlen az eszköz jövőbeli alkalmazhatóságának feltárására.
Saját publikációk, hivatkozások,
linkgyűjtemény
Kapcsolódó saját publikációk listája:
[J1] Á. Szabó, Z. Várallyay, Numerical Study on the Saturable Absorber Parameter Selection in an Erbium Fiber Ring Oscillator. IEEE Photon. Techn. Lett. 24 (2), 122-124. old. (2012)
[J2] Á. Szabó, Z. Várallyay, Linewidth Investigation and Modeling of a High Power Yb-doped Fiber Laser. Optical Fiber Technology (under acceptance)
[J3] Á. Szabó, B. J. Puttnam, D. Mazroa, S. Shinada and N. Wada, Investigation of an All-Optical Black-Box PPLN-PPLN BPSK Phase Regenerator. IEEE Photon. Techn. Lett. 24 (22), 2087-2089. old. (2012)
[J4] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada and N. Wada, WDM Crosstalk in Periodically Poled Lithium Niobate based PSAs. Opt. Express (under acceptance)
[J5] Z. Várallyay, K. Saitoh, Á. Szabó, R. Szipőcs, Photonic bandgap fibers with resonant structures for tailoring the dispersion. Opt. Express 17 (14), 11869-11883. old. (2009)
[J6] Á. Szabó, Sz. Zsigmond, T., Cinkler, Optimal Signal Power in CWDM Optical Networks Considering Physical Effects. The Mediterranean Journal of Electronics and Communications, Invited paper, Vol. 6, No. 2, 65-71. old., 2010
[J7] Á. Szabó, Sz. Zsigmond, Determining the Optimal Signal Power Based on Physical Effects in CWDM Optical Networks. Infocommunications Journal, Invited paper, Hungary, vol. LXIII., 2008/7, 55-59. old.
[J8] Szabó Áron, Zsigmond Szilárd, Optikai jelszint meghatározása CWDM hálózatokban a fizikai hatások figyelembevételével. Híradástechnika, 63. kötet, 43-48. old., 2008
[C1] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada and N. Wada, Multi-channel phase squeezing in a PPLN-PPLN PSA. Optical Fiber Communication Conference (OFC), OSA Technical Digest (Optical Society of America, 2012), paper OW3C.6
[C2] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada and N. Wada, Signal-Signal Crosstalk Measurements in a PPLN-PPLN PSA with Narrow Channel Spacing. The 17th OptoElectronics and Communications Conference (OECC), paper accepted on 4th May, 2012
[C3] Z. Várallyay, K. Saitoh, Á. Szabó, K. Kakihara, M. Koshiba and R. Szipőcs, Reversed dispersion slope photonic bandgap fibers and femtosecond pulse propagation. OFC/NFOEC in San Diego, California, USA, 22-26 March 2009
[C4] Á. Szabó, Sz. Zsigmond, T. Cinkler, Impact of Physical Effects onto the Optimal Signal Power in CWDM Optical Networks. 6th IEEE, IET International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP)in Graz, Austria, 23-25 July, 2008
Linkgyűjtemény:
http://www.nict.go.jp/en/about/
http://www.thorlabs.com/catalogpages/693.pdf
http://aries.ucsd.edu/LMI/TUTORIALS/polarization.pdf
http://www.covesion.com/support/ppln-tutorial.html
http://www.optics.rochester.edu/users/gpa/nlfo_1h.pdf
Hivatkozások:
[1] J. W. Nicholson and D. J. DiGiovanni, High-Repetition-Frequency Low-Noise Fiber Ring Lasers Mode-Locked With Carbon Nanotubes. IEEE Photon. Techn. Lett. 20 (24), 2123-2125. old. (2008)
[2] T. Tsai, Y. Fang, and S. Hung, Passively Q-switched erbium all-fiber lasers by use of thulium-doped saturable-absorber fibers. Opt. Express 18, 10049-10054. old. (2010)
[3] T. Schreiber, B. Ortaç, J. Limpert, and A. Tünnermann, On the study of pulse evolution in ultra-short pulse mode-locked fiber lasers by numerical simulations. Opt. Express 15, 8252-8262. old. (2007)
[4] C. H. Henry, Theory of the linewidth of semiconductor lasers. IEEE Journal of Quantum Electronics 18 (2), 259-264. old. (1982)
[5] R. Slavík, F. Parmigiani, J. Kakande, C. Lundström, Martin Sjödin, Peter A. Andrekson, Ruwan Weerasuriya, et al. All-optical phase and amplitude regenerator for next-generation telecommunications systems. Nat. Photon. 4, 690-695. old. (2010)
[6] Z. Tong, C. Lundström, P. A. Andrekson, C. J. McKinstrie, M. Karlsson, D. J. Blessing, E. Tipsuwannakul, B. J. Puttnam, H. Toda and L. Grüner-Nielsen, Towards ultrasensitive optical links enabled by low-noise phase-sensitive amplifiers. Nat. Photon. 5, 430-436. old. (2011)
[7] Cotter, D., Manning, R., Blow, K., Ellis, A., Kelly, A., Nesset, D., Phillips, I., et al., Nonlinear Optics for High-Speed Digital Information Processing. Science 286 (5444), 1523-1528. old. (1999)
[8] M. Lax, Classical Noise. V. Noise in Self-Sustained Oscillators. Phys. Rev. 160 (2), 290-307. old. (1967)


