 |
BMe Kutatói pályázat |

|
BME Vásárhelyi Pál Építőmérnöki és Földtudományi Doktori Iskola
BME Építőmérnöki Kar, Építőanyagok és Mérnökgeológia Tanszék
Témavezető: Dr. Zsigovics István
Visszapattanási keménység és nyomószilárdság konstitutív modellje betonokra – Egy hatvan éve nyitott kérdés megválaszolása
A kutatási téma néhány soros bemutatása
Tartósságánál fogva a fenntartható építés folyamatának egyik kiemelten fontos végterméke és az épített emberi környezet legnagyobb mennyiségben felhasznált teherhordó szerkezeti anyaga a vasbeton.

1. ábra: Beton felhasználása az építőiparban
A vasbetonszerkezetek tervezésében a beton nyomószilárdsága a mérnöki számítások legfontosabb bemenő adata. A beton nyomószilárdságát (fc) szabványos, öntött próbatesten vagy a szerkezetből kifúrt, henger alakú ún. magmintákon törőgépben tönkremenetelig terhelve határozzuk meg.
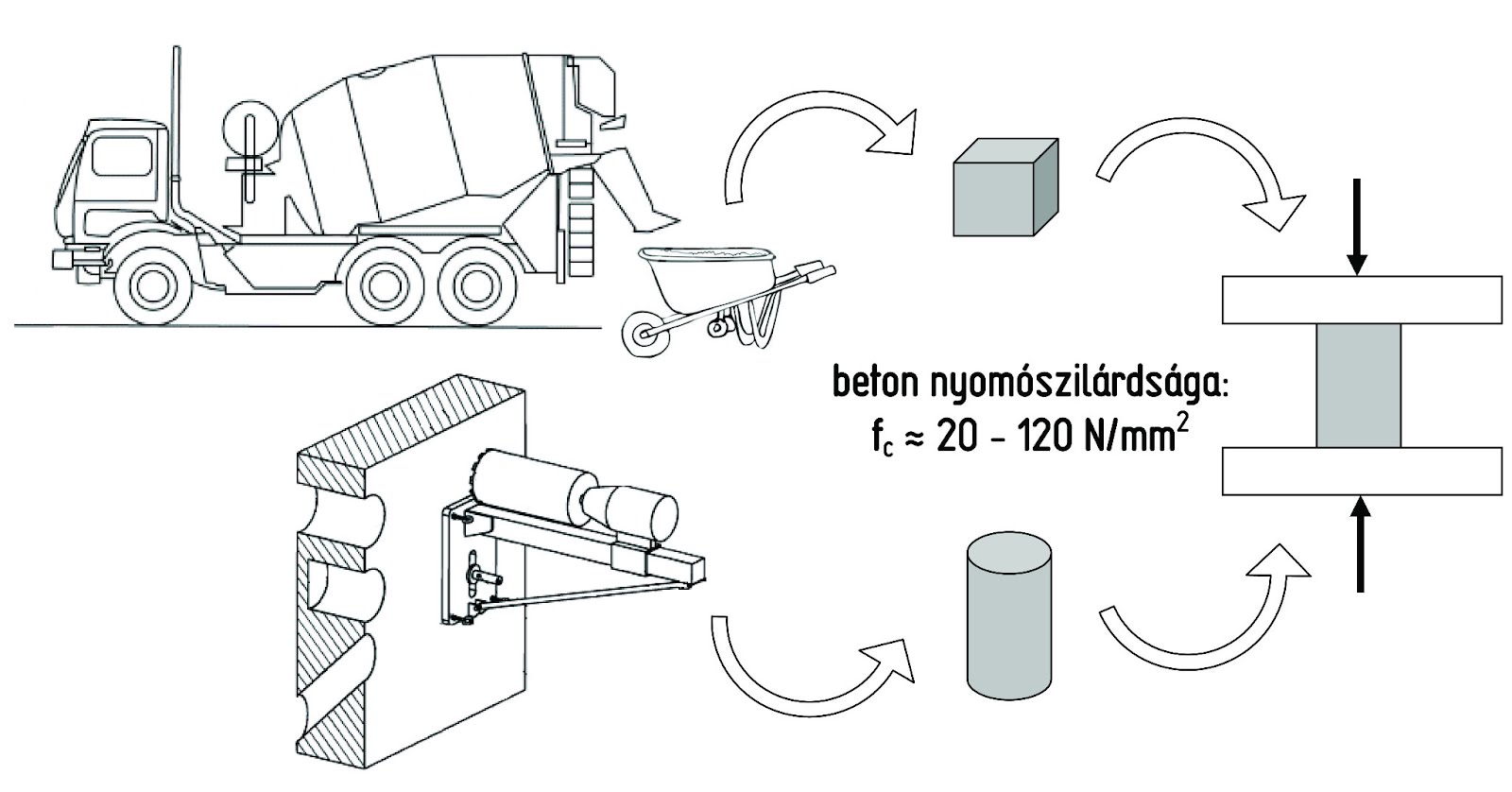
2. ábra: Beton-nyomószilárdság vizsgálatának folyamata
Az öntött próbatestek hátránya, hogy tulajdonságaik nem mindig azonosak a szerkezetbe bedolgozott betonéval, a magminták kifúrása pedig nem minden esetben végezhető el (például a szerkezet állékonyságának veszélyeztetése vagy a vizsgálni kívánt szerkezeti elem rossz megközelíthetősége miatt).
Elméletileg mindkét hiányosság kiküszöbölhető a roncsolásmentes diagnosztikai eszközök használatával. A legsikeresebb szilárdságbecslő módszerek olyan elve(ke)t használnak ki, amely(ek) a beton nyomószilárdságát is meghatározó tényezők egyéb közvetlen vagy közvetett következményeit teszik mérhetővé, vagy némely esetben kismértékű helyszíni roncsolással valósítanak meg szilárdságbecslést. Ezek közé tartozik a jelen kutatás tárgyát is képező egyik klasszikus, a beton felületi keménységmérésén alapuló roncsolásmentes szilárdságbecslő módszer, amely az építőiparban az 1950-es években vált népszerűvé.
A kutatóhely rövid bemutatása
A BME Építőmérnöki Karának Építőanyagok és Mérnökgeológia Tanszéke főként szerkezeti anyagok tulajdonságainak oktatásával és kutatásával foglalkozik. Tanszékünk a BME öt karán lát el oktatási feladatokat és az Építőmérnöki Kar legnagyobb laboratóriumának működtetésével jelentősen hozzájárul az anyagtulajdonságok jobb megértéséhez. Tudományos munkánk során folyamatosan szem előtt tartjuk a laboratóriumi és elméleti kutatómunka együttes alkalmazásának fontosságát, amelyre az anyagtudományokban különösen nagy szükség van. Laboratóriumunk több mint 50 vizsgálatra NAT akkreditált státusszal is rendelkezik. Tanszékvezetőnket, Balázs L. György professzor urat 2010 májusában a több mint fél évszázados múlttal rendelkező, 5 kontinenst, 42 tagországot magában foglaló fib Nemzetközi Betonszövetség elnökévé választották.
A kutatás történetének, tágabb kontextusának bemutatása
A keménységmérés egy megalapozott, több évszázados múltra visszatekintő roncsolásmentes anyagvizsgálati módszer. A keménységmérés volt az első anyagvizsgálati próbálkozás a mérnöki tevékenységben az 1600-as években, jóval a szisztematikus, laboratóriumi anyagvizsgálat kialakulása előtt. Az anyagok keménységének elméleti kutatását Heinrich Hertz úttörő kontaktmechanikai munkája indította el az 1880-as években. Ennek nyomán a képlékeny benyomódási keménységmérési módszerek (Brinell, Vickers, Knoop stb.) sokasága fejlődött ki, amelyeket más szakterületeken napjainkig alkalmaznak helyszíni vizsgálatokhoz is.
E módszerektől eltérően, a betonok felületi keménységmérése a rugalmas visszapattanás elvét használja fel. Az 1950-ben kifejlesztett vizsgáló eszköz (feltalálója után hazánkban Schmidt-kalapácsként ismerik) használata rendkívül egyszerű, ez kedvezett a gyors elterjedésének. Napjainkban a beton felületi keménységének vizsgálatához a rugalmas visszapattanás elvét alkalmazó Schmidt-kalapácsok tekinthetők a legelterjedtebben használt szilárdságbecslő eszközöknek.


3. ábra: A Schmidt-kalapács használata és belső szerkezete
A vizsgálat elve, hogy a készülékben lévő munkarugó egy ütőtömeget mozgásba lendít, amely a felületre merőlegesen tartott, íves kontaktfelületű ütőszondán keresztül, adott energiával megüti a vizsgált felületet.
A keménység mérőszáma a visszapattanási érték (R): a mozgó tömeg visszapattanás közben megtett útjának (xr) és ütés közben megtett útjának (x0) a hányadosa, R = xr/x0 × 100.
Ki kell hangsúlyozni, hogy a Schmidt-kalapácsok a felületi keménységre vonatkozóan egy olyan relatív mérőszámot, a visszapattanási értéket adják eredményül, amely a keresett jellemzővel, a beton nyomószilárdságával látszólag csak empirikus kapcsolatba hozható. A téma szakirodalma rendkívül gazdag, az elmúlt több mint 60 évben publikált több száz szakcikk és tanulmány áttanulmányozását követően azonban arra a megállapításra jutottam, hogy a beton nyomószilárdsága és a Schmidt-kalapács visszapattanási értéke között fennálló kapcsolat elméleti háttere hiányzik, és a szakirodalomban fellelhető függvénykapcsolatok egymástól való jelentős eltérése elemzésre és magyarázatra szorul. Az eltérés részben érthető, hiszen a beton makroszkopikus értelemben heterogén, többfázisú, kapilláris pórusszerkezettel és időben változó tulajdonságokkal rendelkező anyag.
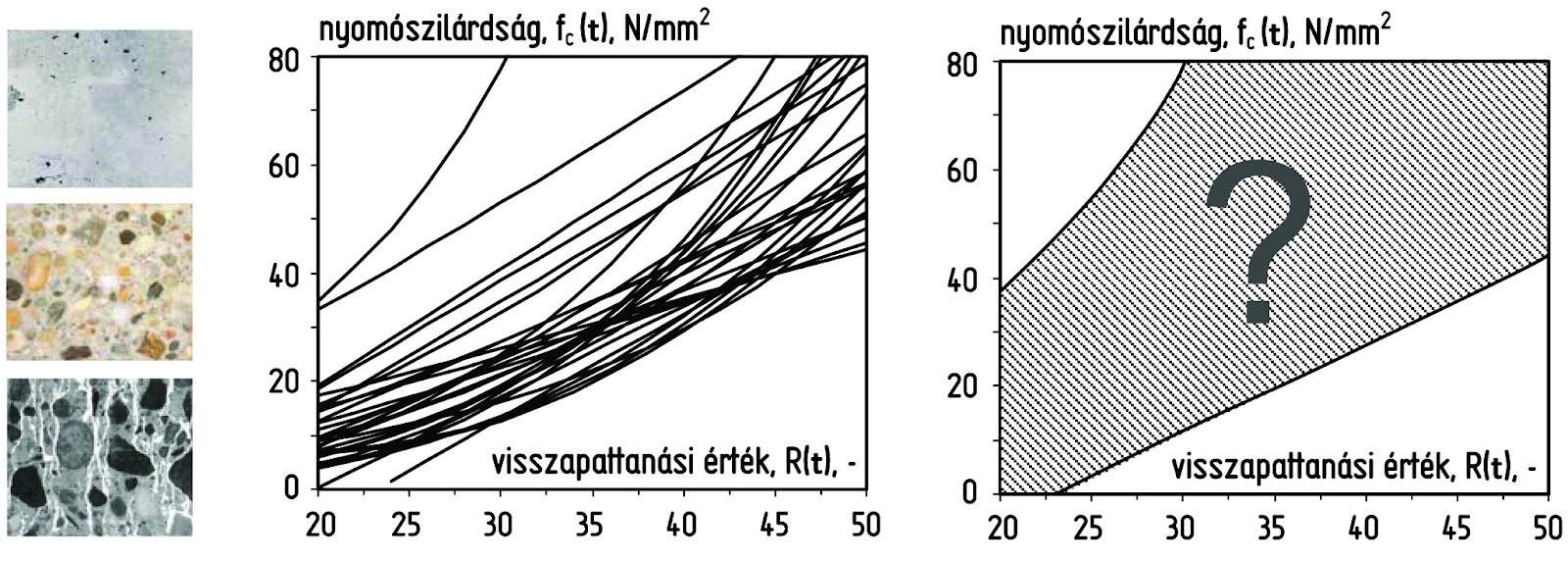
4. ábra: A szakirodalomban található fc(t) – R(t) függvénykapcsolatok
A kutatás célja, a megválaszolandó kérdések
Megfigyelhető a szakirodalomban, hogy a betonok nyomószilárdsága és visszapattanási értéke között feltételezett közvetlen függvénykapcsolatot egy heteroszkedasztikus (azaz a függő változóban a független változó növekedésével növekvő szórású) adathalmazra illesztett középgörbével igyekeznek megadni. Sok esetben ezeknek a függvényeknek az előállítása lineáris regresszióval történik, miközben a lineáris regressziót szigorúan véve csak a homoszkedasztikus (azaz a függő változóban állandó szórású) adathalmazokra lenne szabad alkalmazni. Több szempontból is megkérdőjelezhető a betonok nyomószilárdságának és visszapattanási értékének ilyen módon történő ábrázolása, már csak azért is, mert a független változó és a függő változó között ok-okozati kapcsolat nem áll fenn. Mindkét jellemző ugyanazon hatásoknak a következményeként alakul ki.
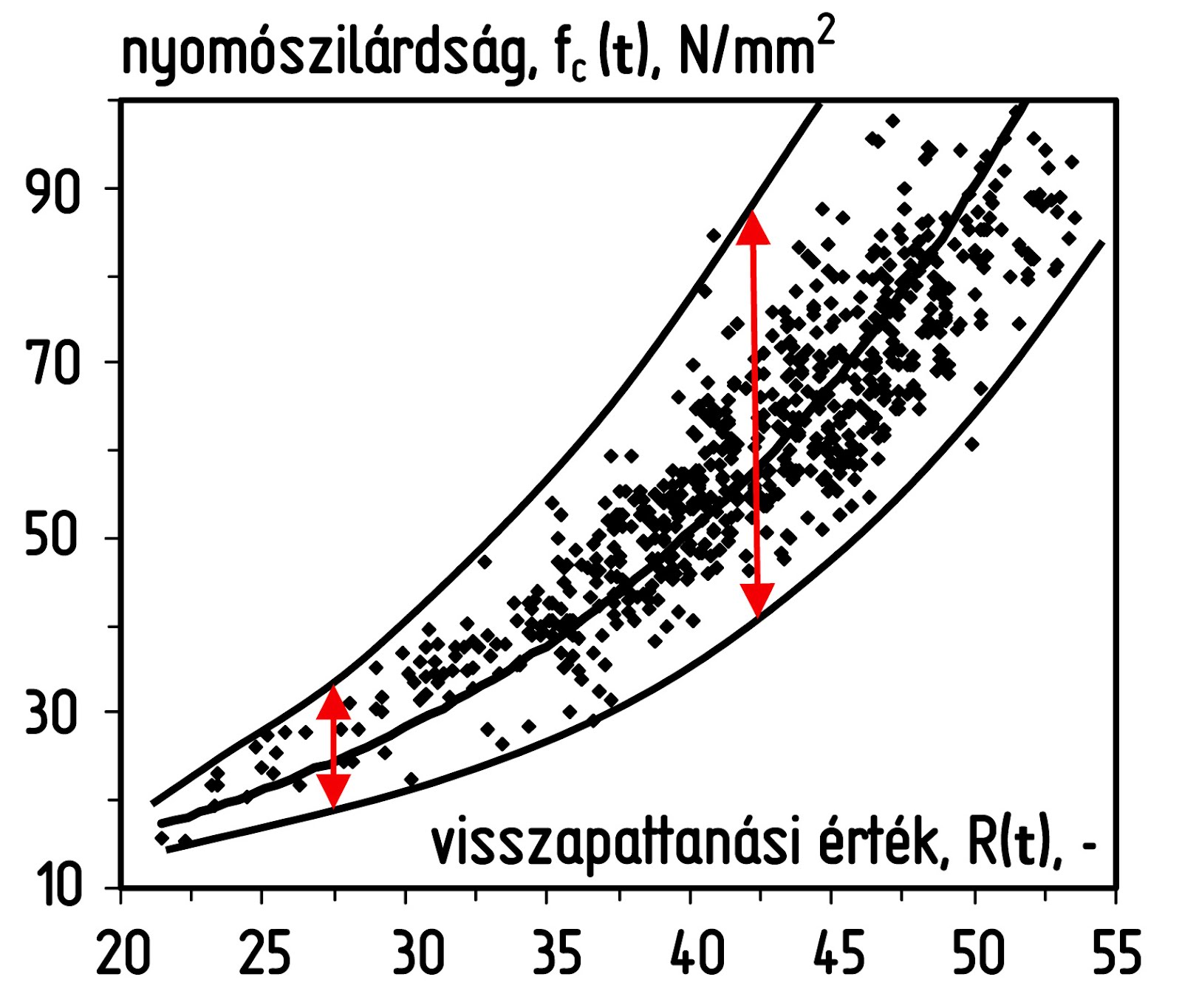
5. ábra: fc(t) – R(t) látszólagos heteroszkedasztikus kapcsolata
Tapasztalati tény, hogy a betonok nyomószilárdságának szórása a beton elkészítésének minőségétől függ, és nem a beton átlagos nyomószilárdságától. Tehát azonos gondossággal elkészített, de különböző nyomószilárdságú betonok szilárdsági szórása azonos mértékűnek várható. Ha a beton nyomószilárdsága és visszapattanási értéke között közvetlen függvénykapcsolatot tételezünk fel, akkor a heteroszkedasztikus mérési adathalmaz megfigyelése a szilárdság szórásával nem indokolható. Ha különösképpen azt is figyelembe vesszük, hogy a gyakorlatban a nagyobb szilárdságú betonok készítése során a minőség-ellenőrzés jellemzően szigorúbb, mint a kisebb szilárdságú betonok esetén, így egy olyan megfigyelés lenne logikailag várható, amelyben a szilárdság szórása a keménység növekedésével nemhogy nő, hanem ezzel ellenkezően, csökken.
Az is tapasztalati tény, hogy a beton felületi keménysége és karbonátosodási mélysége (azon mélység, ameddig az eltelt idő alatt a légkör CO2 tartalma a kapilláris pórusokba diffundálva a portlandit egy részét mészkővé alakította, és ezzel a cementkő kémhatását 8,3 pH értékre változtatta) között van kapcsolat: a karbonátosodás előrehaladása nagyobb keménységet eredményez. A kisebb szilárdságú betonok gázáteresztő képessége nagyobb – ezekben a karbonátosodás nagyobb mélységbe hatol; a nagyobb szilárdságú betonok gázáteresztő képessége kisebb – ezekben a karbonátosodás kisebb mélységbe hatol ugyanannyi idő alatt. Ezt végiggondolva, a nyomószilárdság és a visszapattanási érték változó korú betonok esetén mérhető, összetartozó értékeinek egyazon populációhoz tartozó adatpontokként történő ábrázolása logikailag szintén a heteroszkedasztikus adathalmazzal ellentétes megjelenésű adathalmaz kialakulását valószínűsítené.
PhD kutatásaim kiinduló hipotézise az volt, hogy létezik egy olyan kapcsolat-rendszer a betonok nyomószilárdsága és visszapattanási értéke között, amely rámutat, hogy a két anyagjellemző között a közvetlen függvénykapcsolat felírása nem lehetséges, a megfelelő befolyásoló tényező(k) kiválasztásával azonban olyan, egyértelműen generálható függvénysereg építhető föl, amely a tapasztalati megfigyeléseket kellő pontossággal leírja, és a megfigyelt anomáliákra is magyarázattal szolgál. A hipotézis azt feltételezte, hogy a befolyásoló tényező(k) a cementkő hidratációs fokával kapcsolatban áll(nak).
Módszerek
Kutatásaim első, elméleti részében deduktív elveket követtem. Ahol lehetett, a gondolatmenetemet elméleti megfontolásokra alapoztam, míg más esetekben tapasztalati összefüggéseket tanulmányoztam. Olyan általános érvényű megfigyeléseket és elméleti modelleket vizsgáltam át, amelyek a beton nyomószilárdságával és visszapattanási értékével közvetlenül vagy közvetetten kapcsolatba hozhatók, és a cementkő hidratációs fokára, mint elsődleges okra vezethetők vissza. Mivel a hidratációs fok matematikai modellezése és laboratóriumi meghatározása a gyakorlati alkalmazás egyszerűségre törekvésének elvét általában nem elégíti ki, ezért azt az egyszerűsítést vezettem be, hogy a hidratációs fokot három változóval: a cement típusával, a víz-cement tényezővel (v/c) és a beton korával jellemeztem. Elméleti kutatásaim során az általános törvényszerűségekre koncentrálva a jelenségek véletlenszerűségét nem vettem figyelembe, azaz az egyes befolyásoló tényezők valószínűségi változóként való felírását nem alkalmaztam. A lehetséges belső kapcsolódási pontok feltárása elvezetett egy olyan működési modell hipotéziséhez a beton nyomószilárdsága és visszapattanási értéke között, amely öt általános függvénykapcsolat segítségével képes volt generálni egyes, adott cement típusból, adott víz-cement tényezővel készített, adott korú betonokra vonatkozóan az összetartozó nyomószilárdság – visszapattanási érték adatpontokat. A generátor függvények a következők (amelyek mindegyike empirikus úton validálható): a víz-cement tényező és a beton 28 napos korú nyomószilárdságának kapcsolata; a beton nyomószilárdságának időbeli fejlődése; a beton nyomószilárdságának és visszapattanási értékének kapcsolata 28 napos korban; a karbonátosodási mélység időbeli változása; a karbonátosodási mélység és a visszapattanási érték kapcsolata.
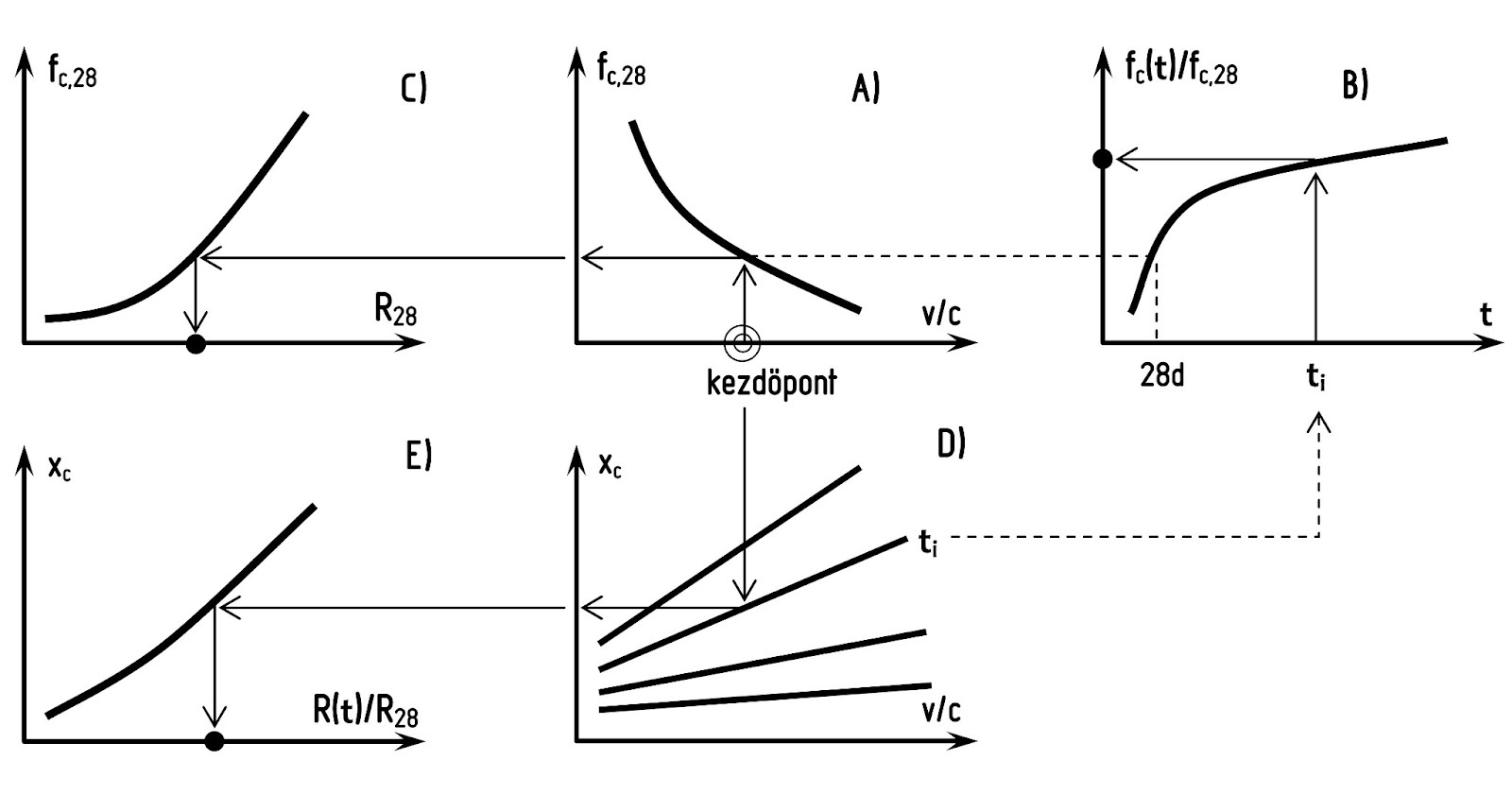
6. ábra: A működési modell sémája (a modellt alkotó 5 függvénykapcsolat)
Parametrikus szimulációval verifikáltam a modell alkalmazhatóságát: tetszőleges függvényparaméterek előzetes felvételével olyan függvényseregeket tudtam generálni, amelyek a valós megfigyelésekhez hasonló eredményeket szimuláltak.

7. ábra: A működési modell általános fc(t) – R(t) eredménye (output): különböző víz-cement tényezőkhöz tartozó, különböző korú állapotokat leíró függvénysereg
Kutatásaim második, laboratóriumi mérési részében a hipotetizált működési modell valós alkalmazhatóságát kívántam igazolni. Induktív elveket követtem, azaz szigorúan szabályozott kísérleti feltételek között, elégségesen nagy számú vizsgálati paraméter bevezetésével, és azok széles spektrumon történő változtatásával hajtottam végre laboratóriumi méréseket nagy számú próbatesten kétszeri ismétléses vizsgálattal, és az egyes megfigyeléseket megfelelő módon grafikusan ábrázolva kerestem a hipotetizált működési modell általános szabályszerűségeit.
Eddigi eredmények
A laboratóriumi kísérletek során a vizsgálati paraméterek számát az egyes vizsgálati sorozatokban fokozatosan növeltem, egyre több paramétert bevonva az analízisbe. Összességében nyolcféle cement típussal végeztem vizsgálatokat. A legtöbb vizsgálati paramétert magában foglaló verifikáló sorozat hét paraméteres, 864 vizsgálati próbatestet (150 mm élhosszúságú próbakockákat) tartalmazó kísérlet volt, amelyben a változó paraméterek a víz-cement tényező, a cementtípus, a cementtartalom, a víztartalom, a cementpéptartalom, az adalékanyag-cement tényező és a vizsgálati kor voltak. A változóktól eltekintve a vizsgálati próbatestekben azonos volt a felhasznált adalékanyag fajtája (dunai homokos kavics), a frissbeton tervezett levegőtartalma (1 V%), a frissbeton konzisztenciája (500±20 mm terülés, folyósító adalékszerrel beállítva), a készítés és bedolgozás módja (acél sablonban vibroasztalon tömörítve), az utókezelés és a tárolás módja (7 napig 20°C hőmérsékletű vízben utókezelve, majd a vizsgálatig laborkörülmények között, 20°C hőmérsékleten, 65% relatív páratartalmú térben tárolva).
A bemutatott eredmények is alátámasztják a működési modell alkalmazhatóságát, amelyet kísérletileg igazoltam számos cementre, széles víz-cement tényező tartományban, többféle vizsgálati korban.
A modell segítségével megérthető a beton Schmidt-kalapácsos visszapattanási értékkel leírt felületi keménysége.
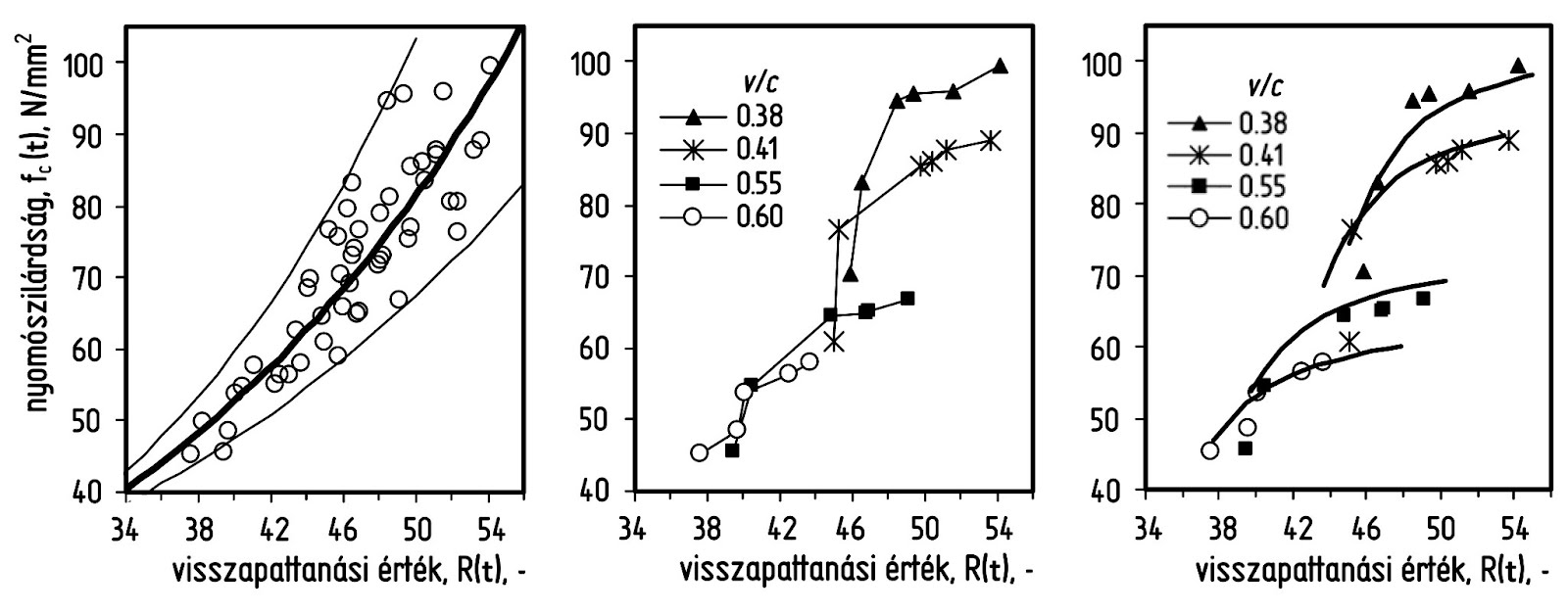
8. ábra: A működési modell kísérleti verifikálása CEM I 42,5 N jelű portlandcement esetére, balról jobbra haladva: a mérési adatpontokat nem választottuk szét; a mérési adatpontokat víz-cement tényező szerint szétválasztottuk; a mérési adatpontok és az illesztett modell együttes ábrázolása
A modell azon túlmenően, hogy jelen formájában is tisztáz több olyan kérdést, amely tisztázatlan maradt az elmúlt 60 évben, átlátható struktúrájának köszönhetően a jövőbeni továbbfejlesztést is lehetővé teszi.
Bár a működési modell rámutatott a beton rugalmas visszapattanási értékkel jellemzett felületi keménységét meghatározó befolyásoló tényezőkre, tisztázni szerettem volna, hogy vajon a különféle módon rugalmas visszapattanást mérő készülékek (L- és N-típusú Schmidt-kalapácsok és Leeb-készülék) mérőszámai, illetve a Brinell-keménység mely mechanikai jellemzővel állnak a legerősebb kapcsolatban. Kutatásaim során betonok széles nyomószilárdsági tartományában és számos eltérő vizsgálati kor mellett tanulmányozva a kérdést igazoltam, hogy a vizsgálat során befektetett energia mennyisége a megkapott keménységi jellemzőn keresztül meghatározza a keménységgel összefüggésbe hozható anyagjellemzőt. Kis energiaelnyelődést eredményező vizsgálat során (például Leeb-készülékkel bármely betonon vagy Schmidt-kalapácsokkal nagy szilárdságú betonon) a keménységi mérőszám a rugalmassági modulussal hozható kapcsolatba. Nagy energiaelnyelődést eredményező vizsgálat során (például Brinell-vizsgálat bármely betonon) a keménységi mérőszám a nyomószilárdsággal hozható kapcsolatba. Köztes állapotokban (például Schmidt-kalapácsokkal végzett vizsgálatok normál betonon) a hatás nem egyértelmű. Vizsgálataim így rámutattak arra, hogy a gyakorlatban leginkább elterjedt szilárdságbecslő eszközöknek, a Schmidt-kalapácsoknak szigorú alkalmazhatósági korlátja van.
Várható impakt, további kutatás
A laboratóriumi kísérletsorozatom eredményei igazolták a beton nyomószilárdsága és a visszapattanási érték közötti működési modell létezésére vonatkozó hipotézisemet. Ezzel sikerült feltárnom és megválaszolnom egy olyan kérdést e szakterületen, amely hosszú ideje várt tisztázásra. A modell rávilágít egy lehetséges elméleti kapcsolatra a két, egyébként időtől függő anyagjellemző között. A modell jól átlátható szerkezete következtében tág teret biztosít a további elméleti és gyakorlati fejlesztésekre. Eredményeimet nemzetközi, impakt faktorral rendelkező folyóiratokban is publikáltam 2011-2012-ben, ami kedvező fogadtatásra talált, és független hivatkozásokat is kapott. További kutatási célom a modell kibővítése valószínűségelméleti irányban, amellyel a gyakorlati alkalmazás számára tehető használhatóbbá.
Kapcsolódó saját publikációk
[1] Szilágyi K. – Borosnyói A. – Zsigovics I. (2012) „Understanding the rebound surface hardness of concrete”, Journal of Civil Engineering and Management, megjelenésre elfogadva
[2] Szilágyi K. (2012) „Hardness studies on porous solids”, Conference of Junior Researchers in Civil Engineering, Budapest, 2012.06.19-2012.06.20. pp. 240-247. nyomtatás alatt
[3] Szilágyi K. – Borosnyói A. – Gyurkó Z. (2012) „Kőszerű anyagok statikus keménységvizsgálata”, Mérnökgeológia-Kőzetmechanika Konferencia 2011, Budapest, 2012.01.26. pp. 297-312.
[4] Szilágyi K. – Borosnyói A. – Zsigovics I. (2011) „Rebound surface hardness of concrete: Introduction of an empirical constitutive model”, Construction and Building Materials, Vol. 25:(5), May 2011, pp. 2480-2487. doi:10.1016/j.conbuildmat.2010.11.070
[5] Szilágyi, K. – Borosnyói A. - Zsigovics I. (2011) „Surface hardness and related properties of concrete”, Concrete Structures, Vol. 12, 2010, pp. 51-57.
[6] Szilágyi, K. – Borosnyói A. – Dobó K. (2011) „Static indentation hardness testing of concrete: a long established method revived”, Építőanyag, Vol. 63. (1-2), 2011, pp. 2-8.
[7] Szilágyi, K. – Borosnyói A. - Zsigovics I. (2010) „Introduction of a constitutive model for the rebound surface hardness of concrete”, Concrete Structures, Vol. 11., 2010, pp. 46-52.
[8] Borosnyói A. - Szilágyi K. (2010) „A hazai Schmidt-kalapácsos betonvizsgálati szabályozásról”, Beton, XVIII. évf. 1. szám, 2010/1, 14-16. oldal
[9] Szilágyi, K. – Borosnyói A. (2009) „50 years of experience with the Schmidt rebound hammer”, Concrete Structures, Vol. 10., 2009, pp. 46-56.
[10] Szilágyi K. – Borosnyói A. (2008) „A Schmidt-kalapács 50 éve: Múlt, jelen, jövő. 1. rész: Módszerek és szakirodalmi összefoglalás”, Vasbetonépítés, X. évf. 1. szám, 2008/1, 10-17. oldal
[11] Szilágyi K. – Borosnyói A. (2008) „A Schmidt-kalapács 50 éve: Múlt, jelen, jövő. 2. rész: Az európai szabványosítás és annak hazai jelentősége”, Vasbetonépítés, X. évf. 2. szám, 2008/2, 48-54. oldal
[12] Szilágyi K. – Borosnyói A. (2008) „A Schmidt-kalapács 50 éve: Múlt, jelen, jövő. 3. rész: Tudományos megfontolások és kitekintés”, Vasbetonépítés, X. évf. 3. szám, 2008/3, 73-82. oldal
[13] Szilágyi K. (2008) „Beton roncsolásmentes szilárdságvizsgálata”, BME Építőmérnöki PhD Szimpózium, Budapest, 2008.11.28. nyomtatás alatt
Tudományos Diákköri Dolgozatok
[1] Gyurkó Z. (2011) „Felületi keménység és szilárdságjellemzõk összefüggéseinek vizsgálata”, BME, 2011. november 16., kari TDK III. helyezés, OTDK jelölés (még nem rendezték meg)
[2] Dobó K. (2010) „Beton felületi keménységmérése statikus és dinamikus módszerekkel”, BME, 2010. november 17., kari TDK II. helyezés, OTDK III. helyezés
