 |
BMe Kutatói pályázat |

|
Csonka Pál Doktori Iskola
BME Építészmérnöki Kar, Szilárdságtani és Tartószerkezeti Tanszék
Témavezető: Dr. Domokos Gábor
Kavicsok morfológiája
A kutatási téma néhány soros bemutatása

Milyen alakúak a kavicsok? - erre az alapvető kérdésre keressük a választ a kutatás során.
A természetben lépten-nyomon előforduló kavicsok változatos formavilága régóta fejtörést okoz a természettudósok számára. A kutatás alapötlete, hogy a statikai egyensúlyok fogalma egy természetes osztályozási rendszert kínál térbeli formák kódolására. Kutatómunkám egyrészt ezen új osztályozási rendszer elméleti matematikai vizsgálatát, másrészt annak feltérképezését foglalja magában, hogy a rendszer segítségével hogyan és milyen mélységben kódolható a kavicsok morfológiája és kopási folyamata a gyakorlatban.
A kutatóhely rövid bemutatása
A Szilárdságtani és Tartószerkezeti Tanszék mechanikai és szerkezettervezési problémák széles körével foglalkozik. A kutatási témák nemcsak acél-, fa-, falazott, kompozit, ponyva-, vasbeton- és vályogszerkezetekkel, hanem stabilitásvesztési problémákkal és földrengési méretezéssel is kapcsolatosak. Kutatási tevékenységünk a mechanika és az alkalmazott matematika számos területére kiterjed, a kavicsok alakja és kopási folyamatai mellett oktatóink foglalkoznak például aszteroidák alakdinamikájával, teknősök morfológiájával, ütközéseknek kitett merev testek stabilitási kérdéseivel is.
A kutatás történetének, tágabb kontextusának bemutatása
A kavicsok geometriája iránt Arisztotelész [6] óta neves tudósok sora érdeklődött [7][8]. A téma ma is az érdeklődés középpontjában áll [9][10][11], hiszen a természetben található, eróziós folyamatok által létrehozott formák vizsgálata maguknak az eróziós folyamatoknak a megértésében segít. A kavicsok alakja információt hordoz az üledékképződés, -szállítás, -lerakódás körülményeiről [12][13], ezáltal segít az ún. fáciesek elkülönítésében.
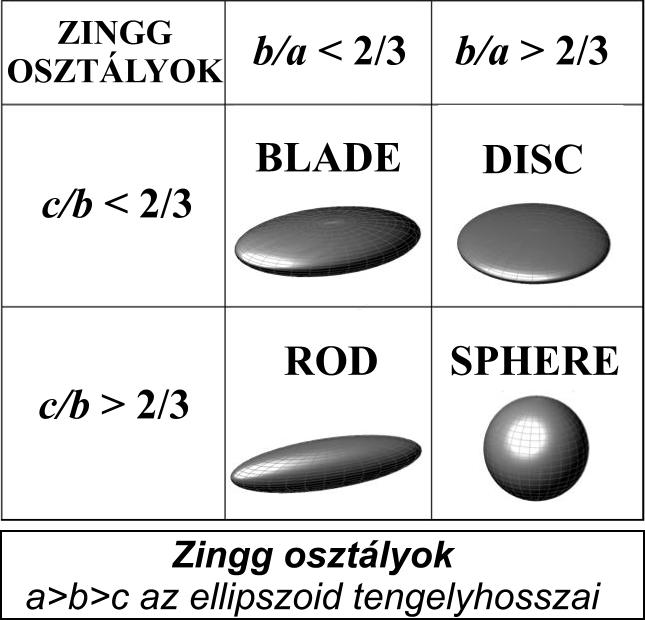
A geológusok számos alak-indexet és ezekre épülő osztályozási rendszert javasoltak a kavicsok morfológiájának leírására [13][14][15][16]. Jelenleg is élénk vita tárgyát képezi, hogy ezek közül melyik a leginformatívabb rendszer [17][18]. Ezek a klasszikus rendszerek hosszméréseken alapulnak, közülük a legelterjedtebb az ún. Zingg-osztályozás [16], amely a kavicsok alakját háromtengelyű ellipszoiddal közelíti, s a tengelyarányok alapján négy osztályba sorolja a formákat. A klasszikus alak-osztályozási rendszerek kétségkívül hasznosnak bizonyultak a gyakorlatban, ám a hosszmérések miatt több, a mérő személy által megbecsült önkényes adatot is tartalmaznak.
A kutatás célja, a megválaszolandó kérdések
A kutatás fő célkitűzése egy olyan új osztályozási rendszer felállítása a kavicsok morfológiájára, amely egyrészt elkerüli a hosszméréseken alapuló osztályozási rendszerekben rejlő bizonytalanságokat, másrészt a gyakorlatban könnyen alkalmazható a geológusok számára. Az új osztályozás a statikai egyensúlyok fogalmára támaszkodik, és ezek száma, típusa, eloszlása, s az egyensúlyok közötti kapcsolatok alapján kódolja a térbeli formákat.
A kód alapja a stabil és instabil egyensúlyi helyzetek száma, mely alapján minden homogén, konvex test egyértelműen osztályba sorolható [19]; ezt nevezzük elsődleges osztályozásnak. A kocka elsődleges osztálya például a {6,8} osztály, mert mind a 6 lapján van egy stabil egyensúly, és mind a 8 csúcsa egy instabil egyensúly. Domokos Gábor és Várkonyi Péter találmánya, a Gömböc [20] az {1,1} osztályba tartozik (mono-monostatikus test).

A morfológia ennél részletesebb leírását kapjuk, ha azt is megvizsgáljuk, hogy mely egyensúlyi pontok szomszédosak egymással. Ezek a szomszédsági viszonyok a kavics felületén egy gráffal írhatóak le, ez a gráf a másodlagos osztályozás alapja.
A fenti osztályozási rendszert érdemes még tovább bővíteni a képzetes egyensúlyok fogalmával. „Nagyítón keresztül” nézve a kavicsok felszínén számos mikroszkopikus méretű egyensúlyt találunk, ezek a kavics valós egyensúlyai. A külső szemlélő szabad szemmel nem képes megkülönböztetni ezeket a valós egyensúlyokat, mert azok csoportokban (falkákban) helyezkednek el a kavics felszínén [3][4]. Helyette a kísérletező magukat a falkákat észleli egy-egy képzetes egyensúlyként.
A kutatás magában foglalja a fent leírt osztályozási rendszer elméleti matematikai megalapozását és az osztályozás kavicsokon történő gyakorlati megvalósítását. Ez utóbbi valós kavicspopulációk statisztikai jellegű vizsgálatát jelenti, mely a kavicsminták geológiailag érdekes helyszíneken történő begyűjtését, osztályozását és az eredmények statisztikai kiértékelését tartalmazza.
A kutatás másik fő célkitűzése a kavicsok kopási folyamatainak megértése és modellezése, különös tekintettel a fent leírt új osztályozási rendszerre. Ez célzott terepi méréseket, laborkísérleteket, illetve numerikus és analitikus modellek vizsgálatát jelenti. Az új, egyensúlyi osztályozási rendszer előnye, hogy csak természetes számokat használ, így minden térbeli formához egyértelműen hozzárendelhető egy kód, és e kód változása nyomon követhető a kopási folyamat során. Célunk annak megértése, hogy egy így előállítható kódsorozattal hogyan követhető le a morfológia változása, és a különböző kopási folyamatokhoz milyen kódsorozat rendelhető.
Módszerek
A képzetes egyensúlyok megszámlálása egyszerű és gyors kézi kísérletekkel elvégezhető kavicsokon. 3D testek felszínén tipikusan 3 fajta egyensúlyt találunk: stabil egyensúlyt, instabil egyensúlyt, illetve nyeregpontot, ezek számát rendre jelölje S, U, illetve H. A Poincare-Hopf tétel [21] alapján gömb topológiájú testekre S+U-H=2, így elegendő a kavics stabil és instabil egyensúlyainak megszámlálása; a nyeregpontok száma ebből már adódik. A kézi kísérlet alapján megadható a kavics képzetes egyensúlyai által meghatározott elsődleges osztály: {S,U}.

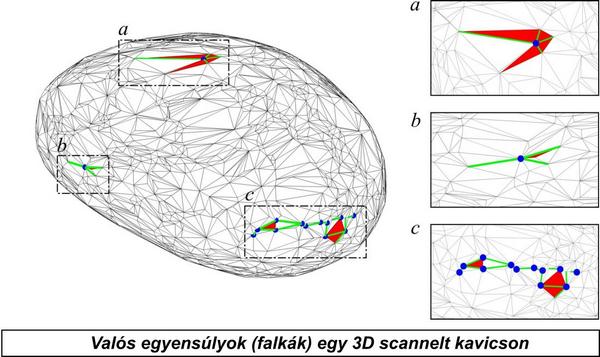
A valós egyensúlyok azonosítása kavicsokon már munkaigényesebb feladat, ellenben az ebből kinyerhető információ is jóval részletesebb. A mikroszkopikus léptékben megjelenő valós egyensúlyok detektálása korszerű 3D szkenneléssel lehetséges. A 0,1 mm pontosságú szkennelést egy CNC gépbe fogatott 3D lézer-szkennerrel végeztük a BME Gyártástudomány és -technológia Tanszékével együttműködve. A szkennelés eredménye egy igen sűrű, háromszögelt poliéderháló, melyen az egyensúlyi pontok számítógép segítségével azonosíthatók.
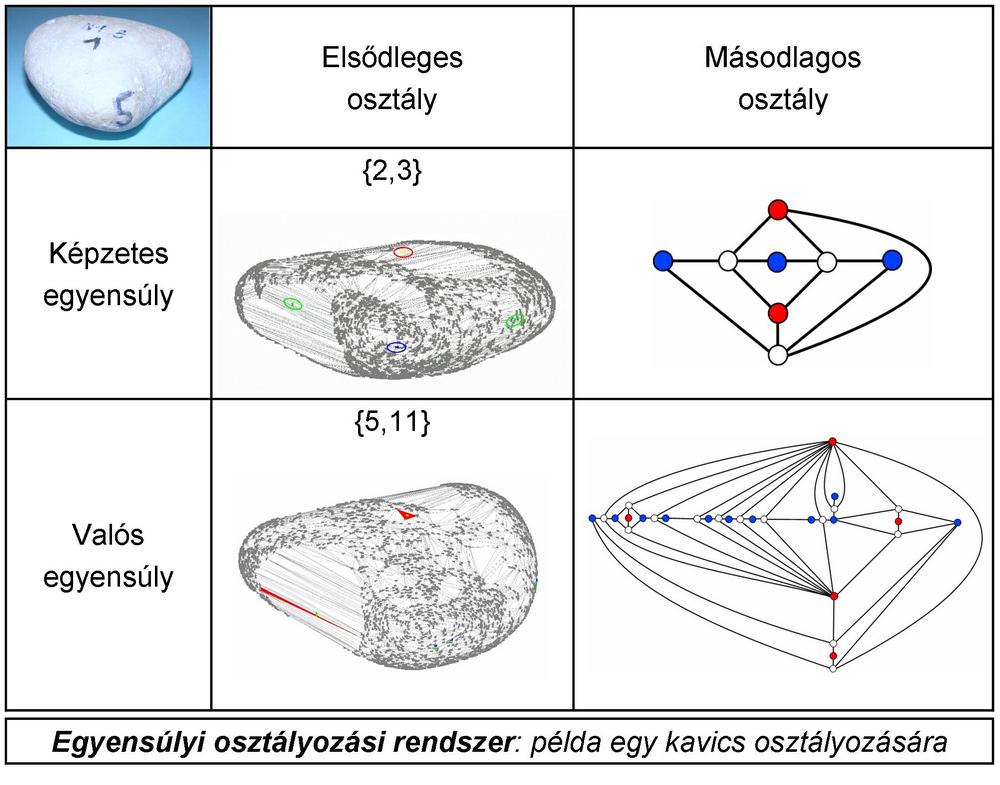
A másodlagos osztályt az egyensúlyi pontok közötti heteroklinikus pályák alkotta ún. Morse–Smale-komplex [22] topológiája határozza meg; ez egy síkba rajzolt gráffal szemléltethető, amelynek csúcsai az egyensúlyi pontok, az élek pedig azt reprezentálják, hogy mely egyensúlyi pontok szomszédosak a kavics felületén. A valós egyensúlyok alkotta gráf egy a Morse–Smale-komplexek témakörében ismert algoritmussal [22] addig egyszerűsíthető, míg a mikroszkopikus léptékű valós egyensúlyok eltűnnek, és csak a makroszkopikus léptékű, a kézi kísérletek során érzékelhető egyensúlyok maradnak hátra – ez a képzetes egyensúlyok alkotta gráf. Geometriailag ez a gráf-egyszerűsítő algoritmus annak feleltethető meg, hogy a poliéder felületet „kisimítjuk”.
Eddigi eredmények
A kézi kísérletek előnye, hogy a képzetes egyensúlyok száma igen gyorsan és egyszerűen, akár terepi körülmények között is megszámlálható, így az új módszer hasznos eszközzé válhat a geológusok kezében. Egyszerűsége ellenére ez a kód meglepően jól jellemzi a kavicsok geometriáját, ugyanis szoros kapcsolat mutatható ki a Zingg-osztályok és az elsődleges képzetes egyensúlyi osztályok között. Mintegy 1000, jól lekopott kavics osztályozása alapján azt találtuk, hogy az egyensúlyi osztályozás egyszerűsített változata 80-90%-os pontossággal tartalmazza mindazokat az információkat, amelyeket a Zingg-osztályozás [1][2], ugyanakkor az új rendszer ennél pontosabb képet nyújt a morfológiáról. Az elsődleges osztályozás például jól jellemzi a koptatottságot, mert világos különbséget tesz például egy gömb, egy tetraéder és egy kocka között, míg a klasszikus, hosszméréseken alapuló rendszerekben, így például a Zingg-rendszerben ezek a formák egyazon osztályba esnek. Az új rendszer különösen alkalmas poliéderek osztályozására, így például kristályalakok új szemléletű rendszerezésére [2].

A fentebb bemutatott 3D szkenneléses módszerrel kimutattuk, hogy a valós egyensúlyok a kavicsok felszínén csoportokban (falkákban) helyezkednek el; egy-egy ilyen falkát a kézi kísérletek során egy-egy képzetes egyensúlyként azonosít a kísérletező. A valós és képzetes egyensúlyok (a mikro- és makroszkopikus egyensúlyok) skálája a gömbhöz közeli kavicsok kivételével jól szétválik [3], így a kézi kísérletek megbízhatóak, a kísérletező nagy biztonsággal el tudja dönteni, hogy a kavicsnak hány képzetes stabil, illetve instabil egyensúlyi pontja van.
A falkákban elhelyezkedő valós egyensúlyok száma szoros összefüggésben van a test lokális geometriájával. Legyen adott egy sima felület egy P egyensúlyi ponttal; megmutattuk, hogy a sima felületet elegendően sűrűn, egyenletesen diszkretizálva, a megjelenő mikro-egyensúlyok száma pontosan megadható P súlyponttól mért távolsága és a felület P-beli két főgörbülete segítségével [4].
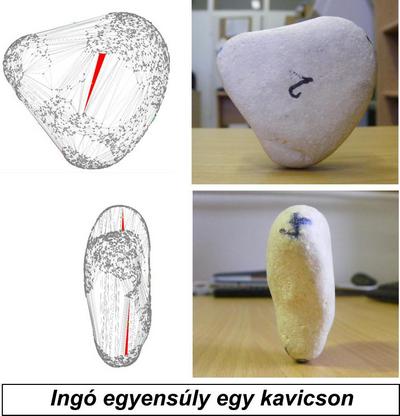
A valós és képzetes egyensúlyok fogalmával szemléletesen magyarázható egy igen érdekes jelenség: az ingókövek látványos egyensúlyi pozíciója. Ezek olyan hatalmas kőtömbök, amelyek az intuíciónak ellentmondó egyensúlyi helyzetben állnak, és nagy tömegük ellenére a legkisebb erőhatásra is mozogni, inogni kezdenek. Szokatlan viselkedésük miatt a múltban számos hiedelem kötődött az ingókövekhez, kapcsolatba hozták például azokat a boszorkánysággal is. Hasonló, de kisebb léptékű alkotásokat mesterségesen is létrehoznak „kőegyensúlyozó-művészek”. A jelenség magyarázatára egy új fogalmat, az ingó egyensúly fogalmát vezettük be [3]: az ingó egyensúly olyan stabil valós egyensúly, amely egy instabil képzetes egyensúlyhoz tartozik. Ez a fogalom világosan magyarázza azt az érzésünket, hogy az ingókövek egyensúlyi helyzete ellentmond az intuíciónak: a mikroszkopikus léptékű stabil valós egyensúlyt a külső szemlélő nem látja, csak azt érzékeli, hogy makroszkopikus léptékben egy instabil helyzetről van szó.
Korábbi kutatómunka [19] bebizonyította, hogy minden elsődleges egyensúlyi osztály nemüres. Felmerül a kérdés, hogy vajon ugyanez igaz-e a másodlagos osztályokra is, vagyis minden, kombinatorikailag lehetséges gráfhoz található-e egy azt reprezentáló homogén, konvex test. Nemrégiben bebizonyítottuk, hogy a válasz igen [5].
Várható impakt, további kutatás
A további kutatás során célzott terepi méréseket, azaz geológiai szempontból érdekes helyszíneken kavicsminták begyűjtését tervezzük. A mintagyűjtés alkalmas helyszíneinek megválasztásával lehetővé válik a különböző üledékképződési, -szállítási, -lerakódási környezetek vizsgálata, a kavicsok kopási folyamatának nyomon követése. Ezzel párhuzamosan a kopási folyamat laborkísérletek útján, illetve numerikus és analitikus modellek segítségével is vizsgálható. Végső célunk a különböző kopási folyamatok megértése és modellezése, különös tekintettel a fent leírt osztályozási rendszerre. 2012 júniusában a University of Newcastle egyetemmel közreműködve Prof. Stephen Fityus geológussal közösen az ausztráliai Williams folyó mentén gyűjtöttem bazaltkavicsokat annak érdekében, hogy végigkövessük a Barrington Tops bazaltfennsíkról származó kavicsok morfológia-változását a folyó forrásától annak torkolatáig, így lehetővé téve a folyóbeli kopási folyamat rekonstruálását.
Az ausztráliai eredményekről bővebben itt olvashat.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája:
[1] G. Domokos, A. Sipos, T. Szabó, P. Várkonyi (2010), Pebbles, Shapes, and Equilibria, Mathematical Geosciences, Vol 42, 29–47.
[2] T. Szabó, G. Domokos (2010), A new classification system for pebble and crystal shapes based on static equilibrium points, Central European Geology, Vol 53/1, 1–19.
[3] G. Domokos, A. Sipos, T. Szabó (2012), The mechanics of rocking stones: equilibria on separated scales, Mathematical Geosciences, Vol 44/1, 71-89.
[4] G. Domokos, Zs. Lángi, T. Szabó (2011), On the equilibria of finely discretized curves and surfaces, Monatshefte für Mathematik, DOI: 10.1007/s00605-011-0361-x
[5] G. Domokos, Zs. Lángi, T. Szabó, The genealogy of convex solids, in preparation, Manuscript PDF on arXiv
Linkgyűjtemény:
BME Szilárdságtani és Tartószerkezeti Tanszék
Az ingókövekről:
Youtube: Bill Dan "kőegyensúlyozó-művész"
[6] Aristotle, in Minor Works, Mechanical Problems, Question 15, translated by W. S. Hett (Harvard University, Cambridge, MA, 2000)
[7] Lord Rayleigh (1942), Pebbles, natural and artificial, Proc. Roy. Soc. London A, Vol 182, 107–118.
[8] F.J. Bloore (1977), The shape of pebbles, Math Geol, Vol 9, 113-122.
[9] W. Ashcroft (1990), Beach pebbles explained, Nature, Vol 346, 227.
[10] M. Lorang, P.D. Komar (1990), Pebble Shape, Nature, Vol 347, 433–434.
[11] T. Yazawa (1990), More pebbles, Nature, Vol 348, 398.
[12] D.J. Graham, N.G. Midgley (2000), Graphical representation of particle shape using triangular diagrams: an Excel spreadsheat method, Earth Surf Proc Land, Vol 25, 1473–1477.
[13] E. Sneed, R.L. Folk (1958), Pebbles in the lower Colorado River, Texas, a study in particle morphogenesis, J Geol, Vol 66, 114–150.
[14] W.C. Krumbein (1941), Measurement and geologic significance of shape and roundness of sedimentary particles, J Sed Petr, Vol 11, 64–72.
[15] C.K. Wentworth (1922), The shapes of beach pebbles, US Geological Survey Professional Paper, Vol 131-C, 75–83.
[16] T. Zingg (1935), Beitrag zur Schotteranalyse, Schweizer Miner, Petrog. Mitt., Vol 15, 39–140.
[17] W. Illenberger (1991), Pebble shape (and size!), J Sed Res, Vol 61, 756.
[18] S.J. Bott, K. Pye (2008), Particle shape: a review and new methods of characterization and classification, Sedimentology, Vol 55, 31–63.
[19] P. Várkonyi, G. Domokos (2006), Static equilibria of rigid bodies: dice, pebbles and the Poincaré-Hopf Theorem, J Nonlinear Sci, Vol 16, 255–-281.
[20] P. Várkonyi, G. Domokos (2006), Mono-monostatic bodies: the answer to Arnold’s question, Math Intell, Vol 28, 34–38.
[21] V.I. Arnold (1998), Ordinary differential equations, 10th printing, MIT Press, Cambridge
[22] H. Edelsbrunner, J. Harer, A. Zomorodian (2003), Hierarchical Morse-Smale complexes for piecwise linear 2-manifolds, Discrete Comput Geom, Vol 30, 87–107.
