BME Matematika- és Számítástudományok Doktori Iskola 

BME TTK, Sztochasztika Tanszék

Témavezető: Dr. Szász Domokos

Matematikai biliárdok és bolyongások aszimptotikus viselkedése 

A kutatási téma néhány soros bemutatása

 

Kutatásaimban a matematikai biliárdokkal (ezeken belül is elsősorban a Sinai biliárdokkal, vagy más néven szóró biliárdokkal), és bizonyos bolyongás modellekkel foglalkozom. A Sinai biliárd egy kaotikus (hiperbolikus, ergodikus, keverő, Bernoulli) dinamikai rendszer, így sok szempontból úgy viselkedik, mintha véletlen lenne. Az utóbbi évtizedekben a tudomány óriási fejlődése lehetővé teszi - ebben a newtoni mechanikai rendszerben - statisztikus fizikai törvények szigorú matematikai levezetését.

A kutatóhely rövid bemutatása

 

Kutatásaimat a BME Matematika Intézet Sztochasztika Tanszékén végzem. A Sztochasztika és a Differenciálegyenletek Tanszékhez kapcsolódik egy dinamikai rendszerekkel foglalkozó csoport, melyet elsősorban Szász Domokos (professzor, MTA alelnöke) és tanítványai alkotnak. Ezen kutatóhelyek rangos voltát jól tükrözik az itt működő szemináriumok: a Sztochasztika szeminárium és a Dinamikai rendszerek szeminárium.

 

A kutatás történetének, tágabb kontextusának bemutatása

 

A Sinai biliárd [S70] definíciója nagyon egyszerű: a d dimenziós tóruszon (általában d=2) adott néhány diszjunkt, sima határú szigorúan konvex halmaz, melyeket szórótesteknek nevezünk. A szórótestek között egy pontszerű részecske szabadon repül, amíg el nem éri az egyik szórótest határát, amikor is onnan visszaverődik (ilyenkor a beesési szög egyenlő a visszaverődési szöggel) (1. ábra). Periodikus Lorentz folyamat alatt ugyanezt a dinamikát értjük – a tórusz helyett a d dimenziós térben periodikusan kiterjesztett szórótest-konfiguráció esetén (2. ábra).

 

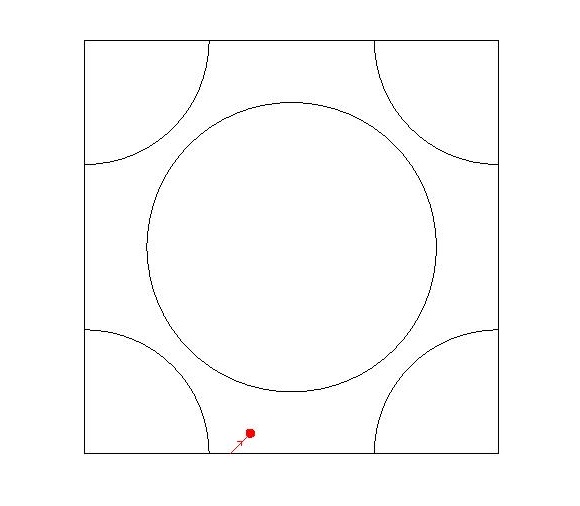
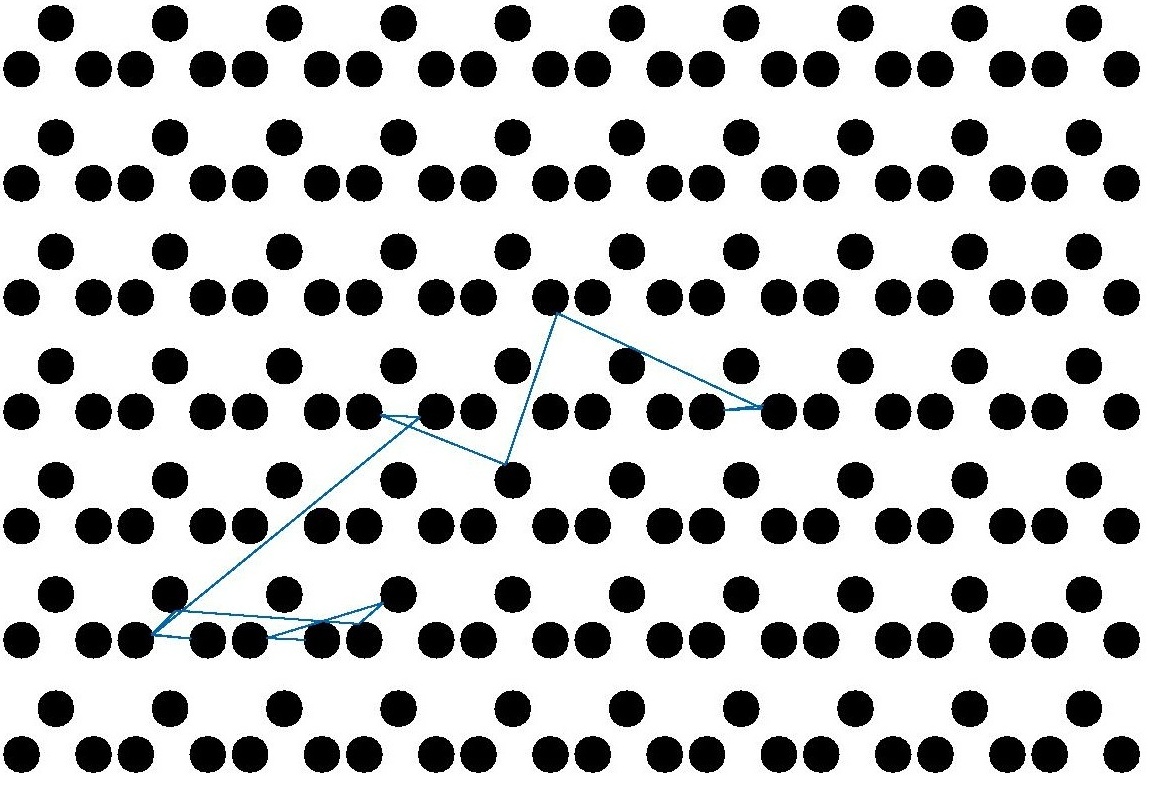
1. ábra: Egy véges horizontú két dimenziós                 2. ábra: 15 ütközéses trajektória egy

Sinai biliárd asztal. Animált változat.                végtelen horizontú Lorentz folyamatban.

 

Brown mozgás

A Brown mozgás durván szólva az a mozgás, melyet egy pohár vízbe ejtett porszem végez. Mivel a porszem rengeteg, különböző irányból érkező molekulával ütközik, ezért a mozgása nem reguláris, véletlenszerű. Ugyanakkor a matematikában gyakran Brown mozgásnak nevezik a Wiener folyamatot (3. ábra) is, ami egy, a fenti fizikai jelenséget modellező matematikai objektum, egy sztochasztikus folyamat.

 

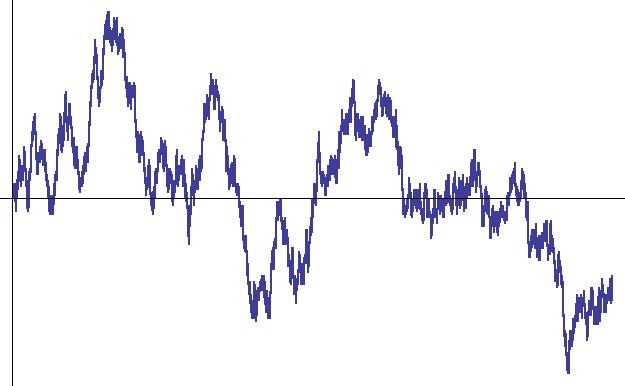
3. ábra: egydimenziós Wiener folyamat egy realizációja

(a vízszintes tengely az időt méri).

 

A Brown mozgás dinamikai elméletének kidolgozásában tehát alapvető fontosságú minden olyan eredmény, amely determinisztikus newtoni rendszerekben – például a Sinai biliárdban - a Wiener folyamat megjelenését igazolja matematikailag precíz módon. Az első ilyen eredmények: [BS80], [BSCh91], a legmodernebb pedig már két, egymással kölcsönható részecskét is tárgyal: [ChD09b]. Ezen kívül ma már egyéb statisztikus fizikai jelenségek (például relaxáció [Y98], hővezetés [GG08]) tárgyalása is lehetséges.

 

A kutatás célja, a megválaszolandó kérdések

 

Kutatásom célja biliárd modellek sztochasztikus tulajdonságainak megértése, bizonyítása.

Az ilyen tulajdonságok szempontjából két lényegesen különböző szórótest-konfiguráció létezik: véges horizont esetén a részecske szabad repülése korlátos (1. ábra), míg végtelen horizontnál nem korlátos (ilyenkor van ütközőmentes végtelen egyenes, 2. ábra).

Az előbb említett Wiener folyamathoz való konvergencia (melyet invariancia elvnek is neveznek) véges horizont esetén diffúzív skálázás mellett igaz, azaz az n ideig tekintett trajektóriát -nel kell skálázni, míg a végtelen horizont szuperdiffúzív, a skálázás  [SzV07, ChD09a].

A kapcsolódó, megválaszolandó kérdések a következők.

1. Igaz-e az invariancia elv, ha a periodicitást egy véges tartományon megsértjük? Ehhez kapcsolódóan érdemes megvizsgálni a részecske visszatérési tulajdonságait egy véges halmazba (mennyi idő alatt tér vissza, mennyit időzik ott, mennyi idő alatt érkezik be ha távolról indult, stb.). Ilyen kérdéseket tárgyalnak a [DSzV08], [DSzV09] cikkek véges horizont esetén; igaz-e hasonló végtelen horizontnál?
2. Mi történik, ha az előző véges perturbációt helyett valamilyen más inhomogenitást tekintünk – akár időben változó szórótest-konfigurációt?
3. Körülbelül mennyi szórótestet látogat meg a részecske n ideig, ha n nagy?
4. A fenti kérdések mindegyikénél szeretnénk megérteni, hogy valóban úgy viselkedik-e a biliárd részecske, mint a megfelelő analóg sztochasztikus modellben egy véletlen bolyongó.

 

Módszerek

Kutatásunk két alapvető tárgya tehát a bolyongások és a Lorentz folyamatok.

 

Bolyongás alatt itt olyan véletlen folyamatot értünk, melyben egy részecske (bolyongó) a d dimenziós négyzetrácson egységnyi időnként lép valamilyen véletlen szabály szerint. A lépésekről feltesszük, hogy azok nem függnek az aktuális pozíciótól. Ha egymástól is függetlenek, akkor a bolyongást egyszerűnek nevezzük. Itt a nem egyszerű bolyongások közül csak olyanokkal foglalkozunk, ahol a lépések eloszlását egy véges halmazbeli belső állapot befolyásolja – belső állapotú bolyongás. (4. ábra)

 

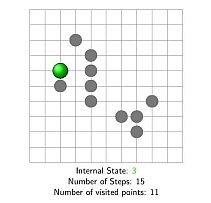
4. ábra: egy belső állapotú bolyongás által

15 lépés alatt meglátogatott pontok. Animált változat.

 

A bolyongások aszimptotikus vizsgálatának alapvető eszköze a Fourier transzformált, vagy más néven karakteriszitikus függvény. A módszer lényege a következő. Ha X, X1, X2, … valószínűségi változók („véletlen számok”), akkor a karakterisztikus függvényeik az uk valós-komplex függvények, melyeket a

 

formula definiálja, ahol E a várható érték, i pedig az imaginárius egység. Az u függvények tulajdonsága, hogy Xn pontosan akkor konvergál gyengén X-hez (azaz, akkor lesz Xn eloszlása közel X eloszlásához), ha  konvergál pontonként -hez, továbbá hasznos, hogy független változók összegének karakterisztikus függvénye a karakteriszitkus függvények szorzata. Így a független esetben aszimptotikus eloszlások sokszor könnyen számolhatók. A módszernek messzemenő általánosításai vannak. Egyszerű általánosítással bizonyíthatók lokális tételek, azaz megmondhatjuk, hogy a bolyongó milyen valószínűséggel tartózkodik sok idő múlva a nullában, így visszatérési tulajdonságokat vizsgálhatunk. Lényegesen nehezebb általánosítással a módszer alkalmazható belső állapotú bolyongásokra is, itt a Fourier transzformált mátrix értékű, sőt, akár determinisztikus rendszerekre is, ahol a karakteriszitkus függvény megfelelője általában valamilyen függvénytéren értelmezett egyparaméteres operátor család.

 

A Sinai biliárd esetén szokás a folytonos idejű dinamika egy Poincaré szelését bevezetni: a folytonos idő helyett csak az ütközési időpontokat tekinteni. Így a fázistér két dimenziós – egy paraméter a szórótest határán vett pozíció, egy paraméterrel pedig a sebességvektor jellemezhető. A diszkrét biliárd dinamika egy kellemes tulajdonsága, hogy hiperbolikus, azaz a fázistéren két közeli pont képe az iterációk során exponenciális sebességgel távolodik egymástól (, melynek oka, hogy az ütközők konvexek). Ugyanakkor kellemetlen tulajdonsága, hogy szakadásos - az érintő trajektóriák miatt. A hiperbolicitás miatt léteznek stabil és instabil sokaságok. Egy instabil sokaság képe kinyúlik (hiperbolicitás), és eltöredezik (szakadások) (5.ábra). Chernov és Dolgopyat módszerének lényege [ChD09b], [Ch06], hogy az úgynevezett növekedési lemmában igazolják, hogy a nyújtás erősebb, mint a töredezés, majd ennek segítségével képesek instabil sokaságokon lévő mértékeket csatolva például exponenciális korrelációlecsengést, vagy invariancia elvet bizonyítani (csatolási lemma).

 

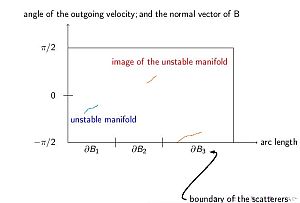
5. ábra: A Sinai biliárd fázistere; egy instabil sokaság képe

néhány instabil görbe uniója.

 

Eddigi eredmények

 

1. A végtelen horizontú lokálisan perturbált síkbeli Lorentz folyamat problémájához kapcsolódóan tekintettük az analóg bolyongás modellt (melyben a végtelen horizontnak megfelelően az n hosszú lépés valószínűsége körülbe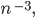lül  [N11b]). Itt igazoltuk a megfelelő visszatérési tulajdonságokat. Azt kaptuk, hogy ez a bolyongó sokkal nehezebben tér vissza az origóba, mint a véges horizontú esetben, hisz itt annak a valószínűsége, hogy n ideig nem tér vissza, körülbelül 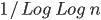, míg ugyanez az érték véges horizont esetén csak 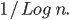 Analóg módon a többi visszatérési tulajdonság is lényegesen eltérő. A bizonyításban (többek között) Fourier transzformálttal igazolunk egy lokális határeloszlás-tételt.

2. Az egyéb inhomogenitásokkal kapcsolatban két cikket említünk: [NSz12], [NSzV12]. Az elsőben egy kétirányban végtelen vízszintes csőben tekintünk egy periodikus biliárd konfigurációt, azonban egy fix pozícióban (például az origóban) egy függőleges falat is beteszünk a csőbe, melyen egy apró lyukat fúrunk. A részecske csak a lyukon keresztül juthat át a falon - így a szórótest-konfiguráció nem homogén - továbbá megengedjük, hogy a lyuk mérete időben is változzon - időbeli inhomogenitás. Ha nincs lyuk, a részecske trajektóriájának skálalimesze a tükrözött Wiener folyamat (6. ábra), ha pedig a lyuk fix méretű, a Wiener folyamat. Az általános esetben véges horizontnál (néhány további feltétel mellett) belátjuk, hogy a diffúzívan skálázott trajektória ezek közös általánosításához, az úgynevezett kvázi tükrözött Wiener folyamathoz konvergál (7. ábra). Az érdekes eset az, amikor a lyuk n idő múlva körülbelül 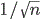  méretű, ekkor lesz a limesz nemtriviális (azaz se nem Wiener, se nem tükrözött Wiener). [NSzV12]-ben tetszőeges időben vett inhomogenitás esetén igazolunk normális eloszláshoz való konvergenciát bizonyos függvényekre, azonban ez a módszer egyelőre csak egy dimenziós rendszerekre érvényes (tehát a biliárdra nem). A bizonyítás során egy, az utóbbi időben népszerű módszert, a martingál közelítést alkalmazzuk.

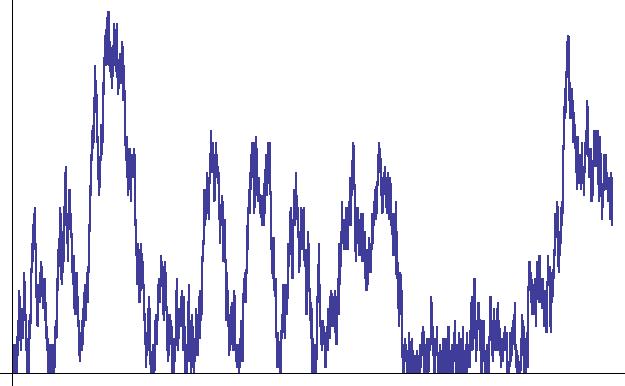
6. ábra: Tükrözött Wiener folyamat - a 3. ábrának megfelelő realizáció.

 

7. ábra: Kvázi tükrözött Wiener folyamat - egy, a 3. ábrának megfelelő realizáció.

 

3. Végül tekintjük egy belső állapotú bolyongó által meglátogatott pontok számát [N11a]. Ez a probléma egyszerű szimmetrikus bolyongásra régóta megoldott [DE51], síkbeli véges horizontú Lorentz folyamatra pedig Péne tárgyalta [P09]-ben. Mi [DE51] összes állítását általánosítjuk, és kitérünk az egy dimenziós esetre is. Az eredmények legérdekesebb része, hogy míg két dimenzióban a bolyongó n ideig nagyjából 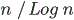  pontot látogat meg, addig 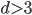 dimenzióban már konstansszor n-et. 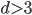Ez összefügg azzal a ténnyel, hogy a bolyongás két dimenzióig biztosan visszatér a kezdőpontjába,  dimenzióban azonban már nem feltétlenül.

 

Várható impakt, további kutatás

A magas dimenziós végtelen horizontú Lorentz folyamat matematikai elmélete ma még szinte teljesen kidolgozatlan. Most Szász Domokossal és Varjú Tamással azt vizsgáljuk, hogyan különböztethetők meg a diffúzív és szuperdiffúzív szórótest-konfigurációk. A fizikusok által is vizsgált sejtés ([ZGNR86], [D12]) az, hogy csak akkor lesz szuperdiffúzió, ha a szórótestmentes térrész maximális dimenziós. Mi Dettmann [D12] első két sejtését akarjuk most bizonyítani.

Tervezzük továbbá a síkbeli végtelen horizontú esetben az invariancia elvet újra bizonyítani a növekedési lemma és az úgynevezett martingál módszer segítségével, melyekkel esetleg később a lokális perturbációk is kezelhetők lehetnek.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

 

[N11a] Nándori, P., Number of distinct sites visited by a random walk with internal states, Probability Theory and Related Fields 150 3 (2011), 373-403.

 

[N11b] Nándori, P., Recurrence properties of a special type of Heavy-Tailed Random Walk, Journal of Statistical Physics, 142, 2 (2011), 342-355.

 

[NSz12] Nándori, P., Szász, D., Lorentz Process with shrinking holes in a wall

Chaos: An Interdisciplinary Journal of Nonlinear Science 22, 2, 026115 (2012).

 

[NSzV12] Nándori, P., Szász, D., Varjú, T., A central limit theorem for time-dependent dynamical systems, Journal of Statistical Physics, 146, 6 (2012), 1213-1220.

 

 

Linkgyűjtemény.

 

A Scholarpedia cikke matematikai biliárdokról 

Krámli András: A káosz matematikusszemmel,Természet Világa 135, 7 (2004)

Chernov és Dolgopyat cikke a 2006-os Nemzetközi Matematikai Kongresszuson hiperbolikus biliárdokról tartott előadás alapján

 

 

Hivatkozások listája.

 

[BS80] Bunimovich L. A., Sinai, Ya. G., Statistical properties of Lorentz gas with

periodic configuration of scatterers, Comm. Math. Phys. 78 (1980/81), 479-

497.

 

[BSCh91] Bunimovich L. A., Sinai, Ya. G., Chernov, N. I., Statistical properties of two-

dimensional hyperbolic billiards, Russ. Math. Surveys 46 (1991), 47-106.

 

[Ch06] Chernov, N., Advanced statistical properties of dispersing billiards, Journal of Statistical Physics 122 (2006), 1061-1094.

 

[ChD09a] Chernov, N.,  Dolgopyat, D., Anomalous current in periodic Lorentz gases with infinite horizon, Russian Mathematical Surveys 64 4 (2009), 651-699.

 

[ChD09b] Chernov, N., Dolgopyat. D., Brownian Brownian Motion–1, Memoirs AMS. 198, No. 927 (2009), pp 193.

 

[D12] Dettmann, C., New horizons in multidimensional diffusion: The Lorentz gas and the Riemann Hypothesis, Journal of Statistical Physics 146 (2012) 181-204.

 

[DSzV08] Dolgopyat, D., Szász, D., Varjú, T., Recurrence Properties of Planar Lorentz Process, Duke Mathematical Journal  142 (2008), 241-281.

 

[DSzV09] Dolgopyat, D., Szász, D., Varjú, T., Limit Theorems for Perturbed Lorentz Processes. Duke Mathematical Journal 148 (2009), 459-499.

 

[DE51] Dvoretzky, A., Erdős, P., Some Problems on Random Walk in Space, Proc. 2nd Berkeley Sympos. Math. Statis. Probab. (1951), 353-367.

 

[GG08] Gaspard, T., Gilbert, T., Heat conduction and Fourier's law in a class of many particle dispersing billiards, New Journal of Physics 10 103004 (2008).

 

[P09] Péne, F., Asymptotic of the number of obstacles visited by a planar Lorentz process, Discrete and Continuous Dynamical Systems, series A, 24 (2009), 567-588.

 

[S70]  Sinai, Ya. G., Dynamical systems with elastic reflections: Ergodic properties of

dispersing billiards, Russ. Math. Surv. 25 (1970), 137–189.

 

[SzV07] Szász, D., Varjú, T., Limit Laws and Recurrence for the Planar Lorentz Process with Infinite Horizon, Journal of Statistical Physics 129 (2007), 59-80.

 

[Y98] Young L.–S. Statistical properties of dynamical systems with some hyperbolicity, Annals of Mathematics 147 (1998), 585–650.

 

[ZGNR86] Zacherl A., Geisel T., Nierwetberg, J., Radons, G., Power spectra for anomalous diffusion in the extended Sinai billiard, Physical Letters 114A (1986) 317-321.