|
BMe Kutatói pályázat |

|
BME Vásárhelyi Pál Építőmérnöki és Földtudományi Doktori Iskola
BME Építőmérnöki Kar, Tartószerkezetek Mechanikája Tanszék
Témavezető: Dr. Bojtár Imre
A szerkezeti üveg anyagszerkezeti hibáinak mechanikai hatása
A kutatási téma néhány soros bemutatása
Az évezredek óta legkülönfélébb célból használt üveg korunkban is kiváló és egyre szélesebb körben alkalmazott építőanyagnak tekinthető. A transzparens építészeti stílusok térhódításával az építészek egyre gyakrabban alkalmazzák az üveget merészebbnél merészebb megoldásokkal. Nem csak bevilágítóként, hanem – a mechanika fejlődésével, a tervezési eljárások megbízhatóbbá válásával és nem utolsó sorban az üveg gyártástechnológiai fejlődésével – homlokzati falként vagy egész terek lefedéseként is megjelenik e transzparens szerkezet.
Az üveg legnagyobb hátránya rideg anyagi viselkedése. Szerkezetének apró hibája nagy feszültségcsúcshoz vezethet, ennek következtében sokszor azonnali tönkremegy, tartalék teherbírása gyakorlatilag elhanyagolható. Ezért nagyon fontos feltérképezni a tartószerkezetként használt üveg mikroszkopikus anyagszerkezeti hibáit. Munkám az ilyen mezo/mikroszintű hibák vizsgálatával és hatásaik tervezési szintű figyelembevételével foglalkozik.
A kutatóhely rövid bemutatása
A Tartószerkezetek Mechanikája Tanszék a Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki Karának kutatási szempontból egyik legaktívabb tanszéke.
A mechanikai alapkutatáson felül több tudományágban is nemzetközi szinten képviselteti magát, ilyenek például a szerkezeti optimalizálás, a biomechanika és az anyagtudományok.
A kutatás történetének, tágabb kontextusának bemutatása
Az üveg – transzparenciájának köszönhetően – napjaink egyik legnépszerűbb építőanyaga. Magának az anyagnak elképesztő szilárdsága van, az építőipari tervezési szabványok jelentős hányada azonban komoly megkötésekkel él az effektív szilárdság és a kellő biztonság megadását illetően, mivel a rideg és hirtelen tönkremenetel jelentősen csökkenti a szerkezeti elem megbízhatóságát.
Az anyagszerkezeti viselkedés okai az amorf molekuláris szerkezetben keresendők. Annak ellenére, hogy a szilícium- és oxigénatomok közti kovalens kötés meglehetősen erős, mivel két atom között jön létre, nem hasonlít a fémes kötésekhez, amelyekben egy elektronfelhő tartja össze a részecskéket. Így a kötés nem rendelkezik jelentős nyírási ellenállással, és ebből következően az anyag alapvetően rideg viselkedésű. Ennek köszönhetően a lokális hibák környezetében a feszültségek nem tudnak leépülni – az anyag nem válik képlékennyé – és így magas feszültségcsúcsok keletkeznek. E feszültségcsúcsok elérhetik az üveg molekuláris szilárdságát és a szerkezeti elem azonnali tönkremeneteléhez vezethetnek.
Ez az oka annak, hogy fontos megismernünk az anyagszerkezeti hibák méretét, alakját és eloszlását, így képet kaphatunk arról, hogy mi játszódik le a tönkremenetel pillanatában. Amennyiben különféle felületkezelések segítségével csökkenteni tudjuk a hibákat, lehetőségünk nyílik az adott elem – makroszkopikusan érzékelhető – effektív szilárdságának a növelésére.
Az egyértelműség kedvéért rögzítjük, hogy a továbbiakban a szóda-mész-szilikát anyagú változatot nevezzük üvegnek.
A kutatás célja, a megválaszolandó kérdések
Az 1. ábrán az üveg négy különböző szintű vizsgálati megközelítése látható. Az első (nano)szinten a molekuláris struktúra kötési energiáit tudjuk elemezni, ezt a feladatot célszerűen „molekuláris dinamikai modellezés” (molecular dynamics) segítségével oldhatjuk meg. A módszert használhatjuk dinamikus mikrorepedés terjedésvizsgálatára amorf szilícium-oxidban; egy 13 milliós elemszámú vizsgálattal például hajtottak végre hasonló szimulációt (Rountree et. al, 2007). Sajnos ez a módszer mai lehetőségeinket figyelembe véve még alkalmatlan a mérnöki gyakorlatban felmerülő problémák megoldására, hiszen mérnökként bennünket elsősorban a makroszintű elemzés érdekel, aminek eredményei a hétköznapi tervezési gyakorlatban is jól alkalmazhatók.
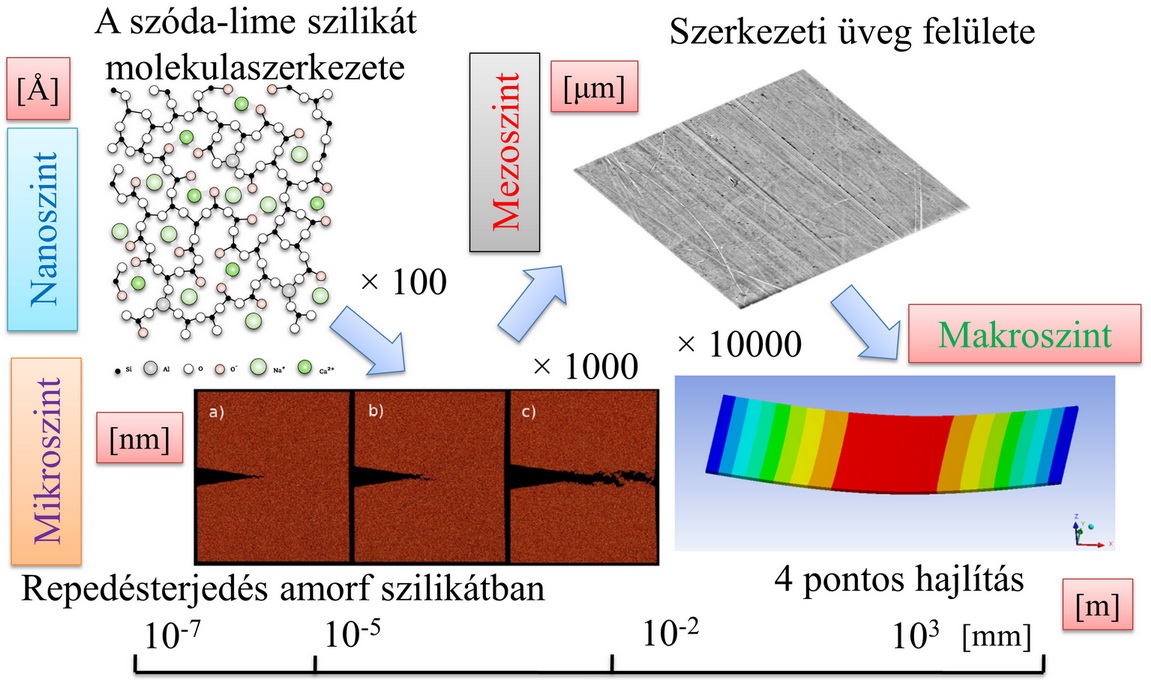
1. ábra: A szerkezeti üveg többszintű modellje
A mikro- és a makroszint közti kapcsolatot egy harmadik típusú, úgynevezett mezoszintű analízis teremti meg. Jelen kutatómunka célja egy kontinuummechanikai modellen alapuló, a mikro- és a makroszintet összekötő vizsgálat végrehajtása, melynek eredményeivel makroszkopikus anyagtulajdonságokat határozunk meg későbbi vizsgálatainkhoz.
A vizsgálat megkezdése előtt fel kellett osztanunk a szerkezeti üvegtáblát vizsgálati régiókra. Első és egyben legjelentősebb része ennek a felosztásnak az üveglap felülete. Ezt a részt éri a legtöbb környezeti hatás, azaz időben változhat a felületi topológia. Második régiónak az élt tekintettük – az élcsiszolásból (zámolásból) eredően ez az üvegtábla leggyengébb része –, a törés többnyire innen indul ki. Harmadik vizsgálati egységünk az üvegtábla térfogatán belüli – a gyártás folyamán, az üvegtestben bennmaradó – zárványokra vonatkozott. A felületi hibákat AFM (atomerő-mikroszkóp), a térfogati zárványokat mikro-CT segítségével vizsgáltuk.
Módszerek
Az elvégzett vizsgálat két nagy részre bontható. Először megvizsgáltuk az üvegtábla mezoszkopikus hibáit, valamint az általuk keltett feszültségcsúcsokat – ehhez numerikus segítségként végeselem módszert használtunk. A második ütemben a térfogati hibák mechanikai hatását vizsgáltuk statisztikus módszerekkel, és próbáltunk olyan egyszerű tervezési irányelveket kialakítani, amellyel pontosabban figyelembe vehető a zárványok keltette feszültségnövekmény.
AFM
A kontakt atomerő-mikroszkóp (AFM) működése egy kantilevernek (konzolnak) is nevezett nagyon érzékeny rugón alapszik, ami egy hegyes formában végződő tű. Ezt a kis hegyet nyomjuk a vizsgált minta felületére egy jól meghatározott laterális erővel. Ezután a mintát egy precíz piezoelektromos szkennerrel mozgatjuk a vízszintes síkban. A kép a kantilever függőleges alakváltozásaiból épül fel, amit lézeres reflexióméréssel határozunk meg.
Mikro-CT
Az inhomogenitások vizsgálatához mikro-CT-t használtunk. A mikro komputertomográfia széleskörűen elterjedt és használt háromdimenziós képalkotási eljárás. A készülék 2D röntgenképeket készít, amelyekből egy célszoftver segítésével felépíthetjük a vizsgált tárgy 3D képét. A képeket egy vagy több detektor rögzíti. Miközben a röntgenforrás mozog a vizsgált tárgy körül, a detektorok 5 fokonként képeket készítenek. Miután a szükséges képeket rögzítettük, egy számítógép rekonstruálja az egyes szeletek képeit, amelyekből elkészíthető a 3D test.
A felesleges torzítások elkerülése érdekében a mintadarabokat oszlop alakúra formáltuk, hogy a sugárnak a lehető legkevesebb üvegen kelljen áthaladnia. Feltételeztük, hogy a mikro-CT-vel készített képek pontos reprezentációi a vizsgált tárgyaknak.
Végeselemes modell
A végeselemes modell felépítéséhez először szükségünk volt a valós geometriára. A mikroszkópok által szolgáltatott adatokat saját szoftver segítségével átalakítottuk a kívánt formátumra, majd előírt elmozdulások – mint peremfeltételek – segítségével egységnyi alakváltozást hoztunk létre a kinagyított, mezoszkopikus modellen.
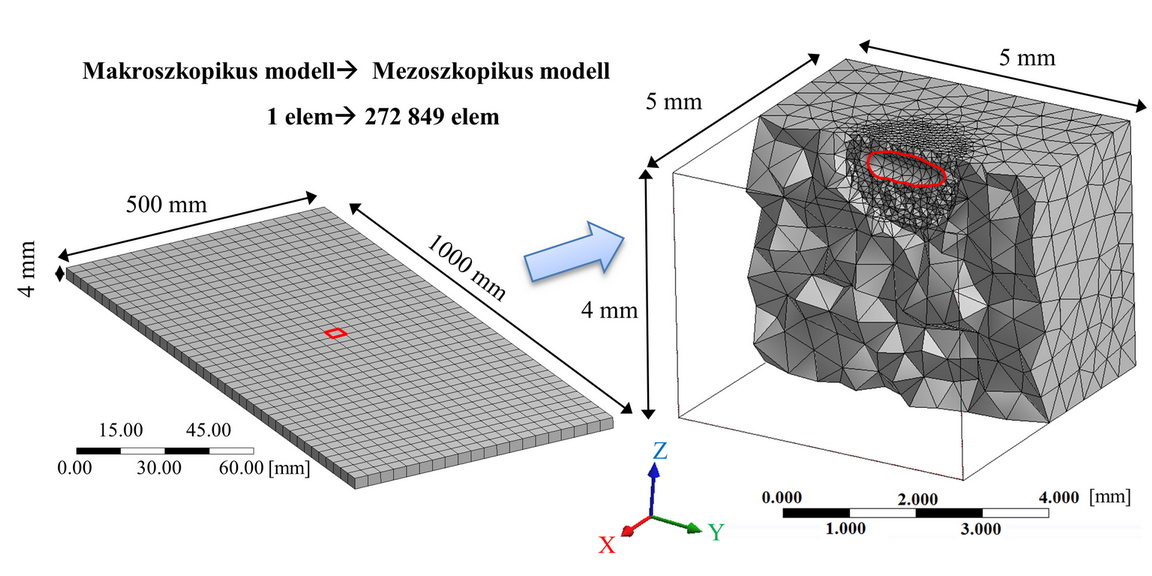
2. ábra: Zárvány vizsgálatához épített modell
A számítások elvégzése után a kapott alakváltozásokat összehasonlítottuk egy tökéletesnek tekintett referenciaelemen számított értékkel, így definiáltuk a hiba által keltett feszültségnövekményt.
Statisztikus homogenizáció
Annak a valószínűsége, hogy a legélesebb zárvány a legnagyobb igénybevétel helyén van, szinte elhanyagolható. Ezért az Eurocode-alapú tervezési irányelvekhez hasonlóan a kutatás céljául egy olyan növekményi érték meghatározását tűztük ki, melynél 95% biztonsággal nem lesz nagyobb, vagyis az érték alulmaradási valószínűsége 0,95. A probléma megoldásához először fel kell írnunk a feszültségkoncentráció sűrűségfüggvényét, majd az ebből képzett eloszlásfüggvénynél a felső integrálási határt úgy kell beállítanunk, hogy a végeredmény éppen 0,95 legyen. A beállított felső határ a keresett feszültséglimit.
Az úsztatott üvegek gyártása során a zárványoknak csak térbeli helyét és méretét regisztrálják, alakjukat nem, a zárvány által keltett feszültségcsúcs azonban elsősorban nem a méret, hanem az alak függvénye. Így az eredi négy valószínűségi változó (három térbeli koordináta és egy alakparaméter) és a feszültségcsúcs közötti transzformációt kellett elvégeznünk. Az átalakítást Monte-Carlo módszerrel hajtottuk végre.
Eddigi eredmények
Ahogy a vizsgálat, úgy az eredmények bemutatását is két részre bontottuk. Első részben a mezoszkopikus hibák keltette feszültségzavarokat ismertetjük, majd az üveglemezekben található térfogati hibák mechanikai hatását figyelembe vevő statisztikai alapon megállapított tényezőt adjuk meg. A tényező segítségével olyan irányelveket és javaslatokat készítettünk, melyek segítségével a hibák hatása nagymértékben csökkenthető.
Felületi karcok hatása
|
|
|
|
|
Gyártósor +7.8 % |
Feldolgozó üzem +36.59 % |
3 éves homlokzat +70.11% |
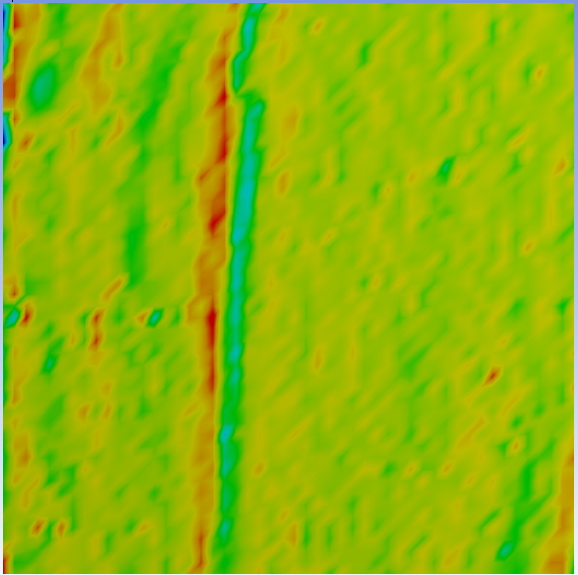
3. ábra: Felületi vizsgálat végeselemes eredményei
A gyártószalagról lekerülő próbatest (Guardian Magyarország Kft.) felülete néhány apró, nanométer mély egyenetlenségtől eltekintve szinte tökéletes volt. (3. ábra)
A második oszlopban lévő eredmények egy a feldolgozóüzemből (OROSházaGLAS Kft.) származó próbadarabról származnak. Jól látható, hogy a karcok mélysége és mennyisége nő, azonban nem a karcok, hanem az apró mélyedések okozzák a maximális feszültség-koncentrációkat.
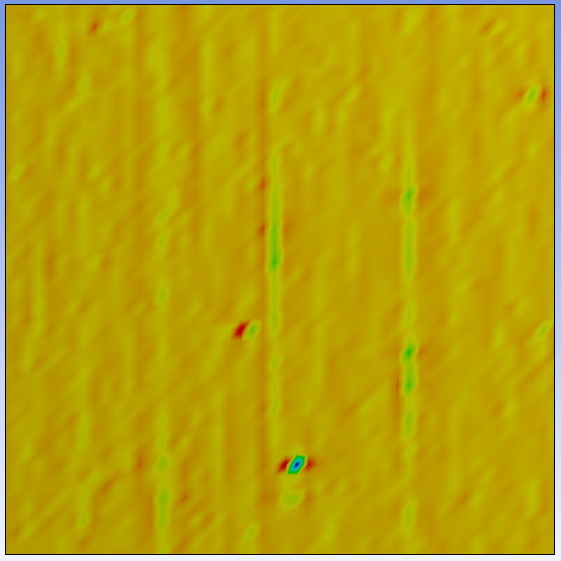
A harmadik oszlopban egy hároméves, homlokzati falként használt üvegdarab eredményei láthatók. Szembetűnő, hogy a karcok mennyisége és hatása is csökken, ezzel párhuzamosan viszont a környezeti hatások okozta apró mélyedések a numerikus szimuláció eredményein már jelentős feszültségcsúcsokat jeleznek. Ez a folyamat a környezeti korrózióval magyarázható. A 4. ábrán további eredmények láthatók a használati idő függvényében.
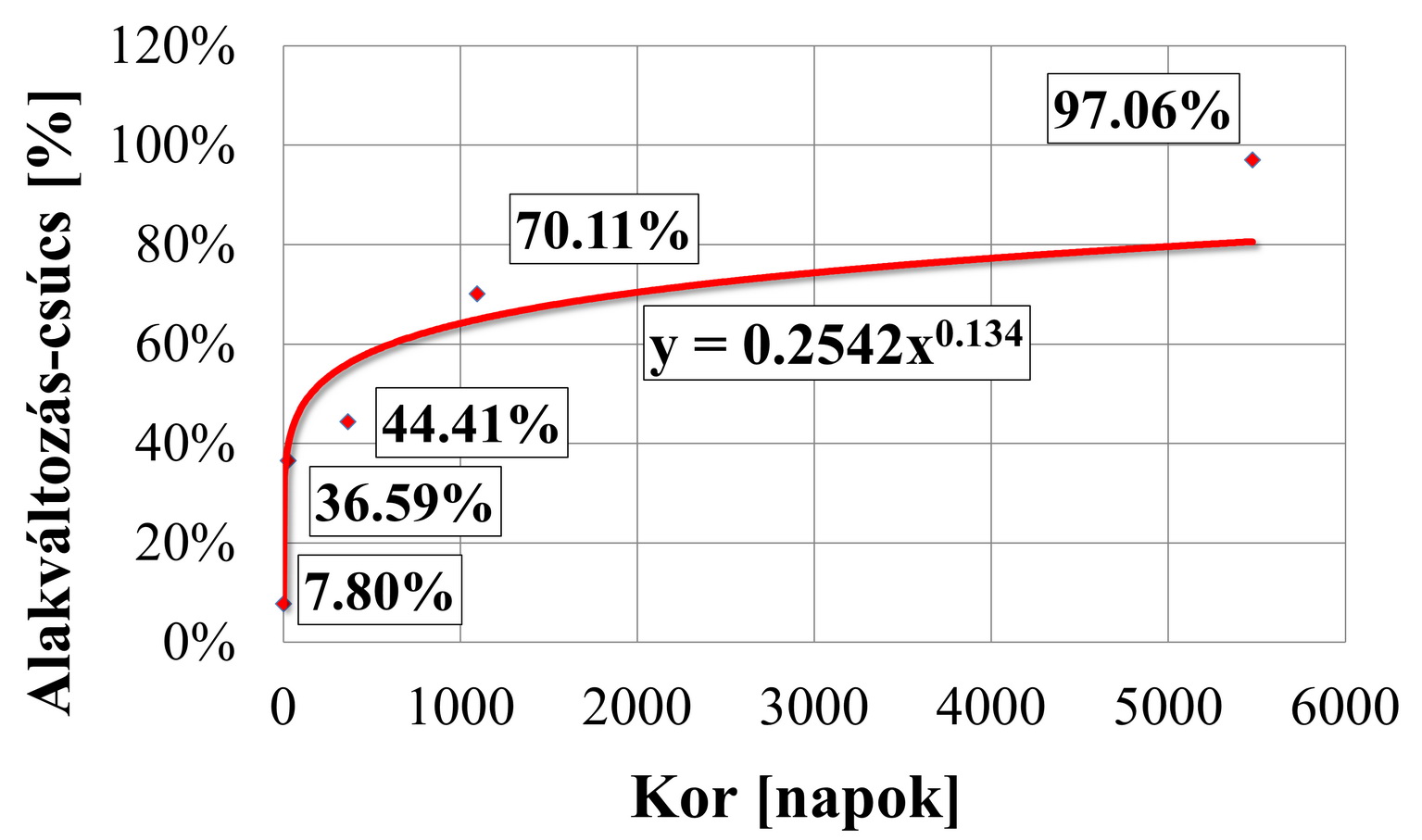
4. ábra: Feszültségnövekmény az üvegfelület korának függvényében
Élmegmunkálásból eredő hibák
A vizsgálat célja, hogy összehasonlítást nyerjünk a különböző felületi megmunkálások keltette feszültségcsúcsokról. A szerkezeti üveglemezek élét a vágás után csiszolni (zámolni) szokták, külön kérésre azonban a zámolás után polírozzák is. Az volt a feladatunk, hogy eldöntsük, mennyire tudjuk a felület egyenetlenségét csökkenteni mechanikai szempontból az utókezeléssel.
|
|
|
|
Csiszolt (zámolt) +352.46% |
Polírozott +157.21% |
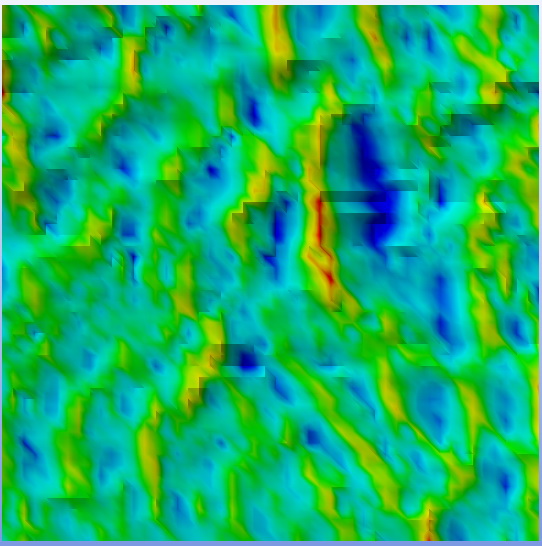
5. ábra: Feszültségnövekmény az éleken a megmunkálás függvényében
Az 5. ábrán jól látható, hogy a polírozott él sokkal egyenletesebb, így a feszültség-növekmény is sokkal kisebb. Végeredményképpen kimutattuk, hogy az utólagos polírozott élmegmunkálás közel 200%-kal csökkentheti az élen kialakuló feszültségeket, így növelve a szerkezeti elem effektív, érzékelhető szilárdságát.
Térfogati hibák keltette feszültségek
A vizsgálathoz Skyscan 1172 mikro-CT-t alkalmaztunk. Kimutattuk, hogy a légzárványok forgási ellipszoid (orsószferoid) alakúak (6. ábra), hiszen az 1600 °C-os olvadékban a légzárványok – a hidrosztatikus állapot miatt – gömbformát vesznek fel és az egyirányú húzástól (úsztatástól) megnyúlnak, ezért legnagyobb főtengelyük mindig párhuzamos az úsztatási iránnyal.

6. ábra: Optikai felvétel az üvegben lévő légzárványról
A gyártótól kapott adatbázis alapján fel tudtuk írni a térbeli sűrűségfüggvényeket (7. ábra), valamint további – optikai mikroszkópos – vizsgálatokkal mérni tudtuk, hogy milyen a legnagyobb és a legkisebb főtengely arányának eloszlása.
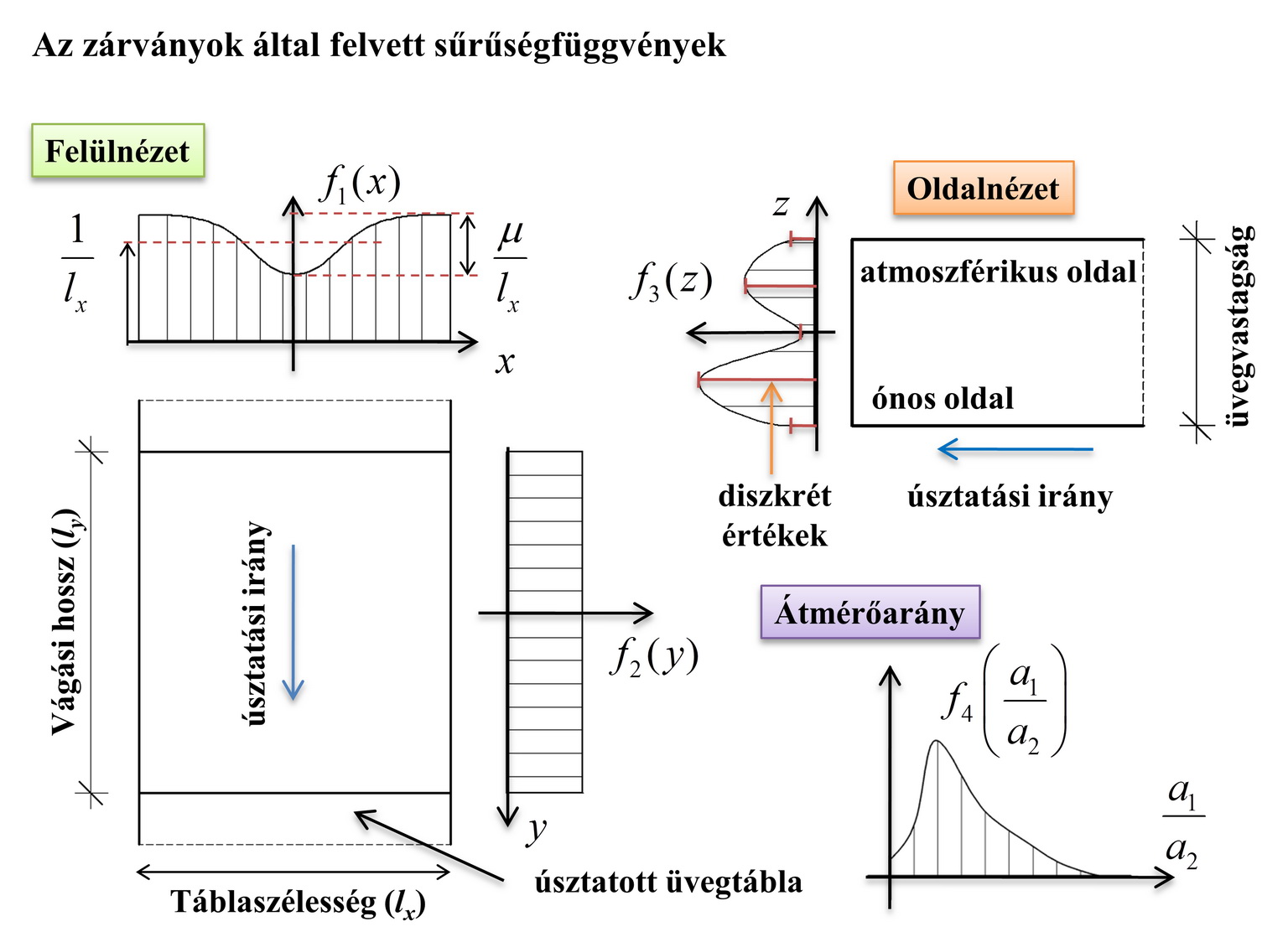
7. ábra: A zárványok sűrűségfüggvényei (három reprezentálja a térbeli elhelyezkedést, egy alakot)
Erre azért van szükség, mert az általuk okozott feszültségcsúcs ennek az alakparaméternek a függvénye. A „Módszerek” szakaszban leírt eljárás alapján definiált tényezővel különböző méretű üvegtáblákat vizsgáltunk. Jól látható a 8. ábrán, hogy a tényező összességében egy mérethatást fejez ki, amely szerint minél nagyobb az üveglap, annál nagyobb a valószínűsége, hogy élesebb hiba van az üvegben.
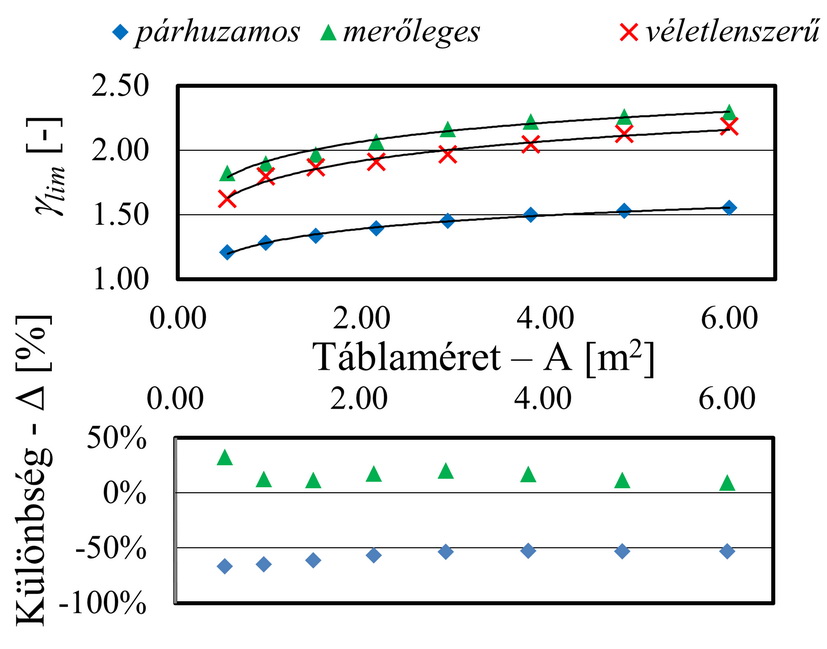
8. ábra: A zárványok mechanikai hatását figyelembe vevő tényező az üveg méretének függvényében
Kimutattuk, hogy ha a zárványokkal párhuzamos a terhelés iránya, úgy átlagosan 50%-kal csökkenthető az általuk keltett feszültségnövekmény. Emellett még több különböző módszert is megalkottunk, melyekkel tovább csökkenthető a térfogati hibák hatása – további eredmények az irodalomban (Molnár et al, 2012) olvashatók.
Várható impakt, további kutatás
A kontinuum-alapú mezoszkopikus vizsgálattal meghatározott anyagjellemzőket egy hibrid – diszkrét- és végeselem-módszerben épített – modellben használjuk fel, melynek célja az edzetlen és az edzett üvegtáblák teljes tönkremenetelének nyomon követése különböző terhelések hatására. A vizsgálat egy numerikus és a modell verifikációját célzó gyorskamerás plusz feszültségoptikai kísérleti összeállításból áll. Ezeket a vizsgálatokat a Dán Műszaki Egyetemmel együttműködve végezzük.
Megjegyezzük, hogy a szerkezeti üvegek tervezéséről szóló európai szabványt (Eurocode) összeállító bizottság a „TUD COST Action TU0905 Structural Glass” a mezoszkopikus vizsgálatot és eredményeit bemutató munkánkat érdemesnek találta a további kutatásokra, és felvette az üvegszilárdság meghatározását célzó munkacsoport fontos témái közé.
Kapcsolódó saját publikációk listája
MOLNÁR G., BOJTÁR I., The effects of the manufacturing inhomogeneities on strength properties of float glass. Mechanics of Materials, 2012.„Publikálásra benyújtva”
MOLNÁR G., VIGH L. G., STOCKER GY., DUNAI L., Finite Element Analysis of Laminated Structural Glass Plates With Polyvinyl Butyral (PVB) Interlayer. Periodica Polytechnica Civil Engineering, Vol. 56, No. 1, pp. 35-42, 2012.
MOLNÁR G., Effect of the Mesoscale Defects on the Strength Properties of Structural Glass, COST Training School “Structural Glass” Student Colloquium, Ghent, Belgium, pp. 15-18. 2012. (ISBN: 978-94-6197-029-9)
MOLNÁR G., MOLNÁR L.M., BOJTÁR I., Preparing a comprehensive analysis of the mechanical classification of structural glass, Materials Engineering - Materiálové inžinierstvo, Vol. 19, pp. 71-81, 2012.
MOLNÁR G., MOLNÁR L.M., BOJTÁR I., Multi-Scale Analysis of Structural Glass, Imaging of The Mesostructure, Journal of Material Testers, Vol. 21, No. 3-4, pp. 1-14, 2012.
MOLNÁR G., BOJTÁR I., Solution of 1D Finite Element Problems With Explicit Time Integration, Architectonics and Architecture, Vol. 40, No. 1, pp. 5-32, 2012.
MOLNÁR G., VIGH L. G., STOCKER GY., Laminált üveglemezek hajlítási teherbírásának vizsgálata, Magyar Építőipar, 62. kötet, 1. szám, 17-23. oldal, 2012.
MOLNÁR G., Experimental and Numerical Examination of Laterally Loaded Laminated Glass, 28th Danubia-Adria-Symposium on Advances in Experimental Mechanics, Siófok, Hungary, pp. 263-264. 2011. (ISBN: 978-963-9058-32-3)
MOLNÁR, G., The Mechanical Behaviour of Laterally Loaded Laminated Structural Glass, 11th Hungarian Conference on Theoretical and Applied Mechanics, Miskolc, Hungary, pp. 1-6. 2011. (ISBN: 978-963-661-975-6)
Linkgyűjtemény
BME Department of Structural Mechanics
Department of Electronics Technology
Journal of the American Ceramic SocietyMechanics of Materials
Hivatkozások listája
[1] Haldimann, M., Luible, A., Overend, M., Structural Use of Glass, Structural Engineering Document 10 IABSE, AIPC, IVBH pp. 85-106. 2008.
[2] Wörner, J.-D., Schneider, J., Fink, A.: Glasbau. Grundlagen, Berechnungen, Konstruktion. Springer-Verlag Berlin Heidelberg New York, p. 66. (2001)
[3] EN 1288-3:2000: “Glass in Building – Determination of the bending strength of glass – Part 3: Test with speciment supported at two points (four-point bending)”, CEN, Brussels; pp. 8-11, (2000)
[4] Rountree C.L., Prades, S., Bonamya, D., Bouchaud, E., Kalia, R., Guillot, C., A unified study of crack propagation in amorphous silica: Using experiments and simulations, Journal of Alloys and Compounds 434–435 (2007)
[5] Kern, W., Puotinen, D.A. Cleaning solutions based on hydrogen peroxide for use in silicon semiconductor technology. RCA Review, June, pp. 187-206, (1970)
[6] Henke, L., Nagy, N., Krull, U.J., An AFM determination of the effects on surface roughness caused by cleaning of fused silica and glass substrates in the process of optical biosensor preparation, Biosensors and Bioelectronics 17, pp. 547-555, (2002). (doi:10.1016/S0956-5663(02)00012-X)
[7] Molnár, L.M.; Mojzes, I.; Nanotechnológia, Műegyetem Kiadó, 2007. 5. fejezet, 75. oldal
[8] Hounsfield G. N.: Computerized transverse axial scanning (tomography): Part 1. Description of system, British Journal of Radiology, 46 , pp. 1016-1022 (1973). (doi: 10.1259/0007-1285-46-552-1016)
[9] Bartuška, M., and co-authors, 2001 Glass Defects Glass Service, Inc.
[10] Benedetti, A., Geotti-Bianchini, F., Fagherazzi, G., Riello, P., Albertini, G., De Riu, L., 1994 SAXS study of the micro-inhomogeneity of industrial soda lime silica glass. Journal of Non-Crystaline Solids. 167, 263-271.
[11] Dyson, F.D., 1981 The potentials of ellipsoids of variable densities. Quarterly Journal of Pureand Applied Mathematics. 25, 259-288.
[12] Eshelby, J.D., 1957 The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 241, 376-396.
[13] Eshelby, J.D., 1959 The elastic field outside an ellipsoidal inclusion. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 252 561-569.
[14] Eshelby, J.D., 1961 Elastic inclusion and inhomogeneities. Progress in Solid Mechanics 2, 89-140.
[15] Ferrers, N.M., 1877 On the potentials of ellipsoids, ellipsoidal shells, elliptic laminae and elliptic rings of variable densities. Quarterly Journal of Pureand Applied Mathematics. 14, 1-22.
[16] Jin, Y., Wang, Z., Zhu, L., Yang, J., 2011 Research on in-line glass defect inspection technology based on Dual CCFL. Procedia Engineering. 15, 1797-1801. 10.1016/j.proeng.2011.08.334
[17] Liu, H.G., Chen, Y.P., Peng, X. Q., Xie, J.M., 2011 A classification method of glass defect based on multiresolution and information fusion. Int. J. Adv. Manuf. Technol. 56, 1079-1090. 10.007/s00170-011-3248-z
[18] Meng, C., Heltsley, W., Pollard, D.D., 2011 Evaluation of the Eshelby solution for the ellipsoidal inclusion and heterogeneity. Computers & Geosciences., 10.1016/j.cageo.2011.07.008
[19] Mura, T., 1987 Micromechanics of Defects in Solids: Mechanics of Elastic and Inelastic Solids. Kluwer Academic.
[20] Peng, X., Chen, Y., Liu, H., Xie, J., Gu, C., 2011 An online defect classification method for float glass fabrication. Glass Technology - European Journal of Glass Science and Technology Part A. 52 (5) 154-160.
[21] Peng, X., Chen, Y., Yu, W., Zhou, Z., Sun, G., 2008 An online defects inspection method for float glass fabrication based on machine vision. Int. J. Adv. Manuf. Technol. 39, 1180-1189. 10.1007/s00170-007-1302-7
[22] Routh, E.J., 1895 Theorems on the attraction of ellipsoids for certain laws of force other than the inverse square. Philosophical Transactions of the Royal Society of London. Series A. 186, 897-950.