 |
BMe Kutatói pályázat |

|
Fizikai Tudományok Doktori Iskola
BME TTK, Atomfizika Tanszék/Fizika Intézet
Témavezető: Dr. Erdei Gábor
Pozitronemmissziós tomográf detektormoduljainak optikai vizsgálata
A kutatási téma néhány soros bemutatása
A 3 dimenziós orvosi képalkotás fontos szerepet tölt be az orvosi diagnosztikában, illetve az anyagcsere folyamatok, idegrendszeri működés és a daganatok kialakulásának kutatásában. Ennek egyik hatékony jövőbeni eszköze a mágneses rezonancia képalkotással (MRI) kombinált pozitron emissziós tomográfia (PET). Ennek az új PET készüléknek azonban új, szilícium technológián alapuló gamma detektormodulokra kell épülnie. Az új típusú detektormodulok fejlesztése sokrétű tervezési, szimulációs és tesztelési feladatot ró a fejlesztőkre, hogy optimalizált eszközök készülhessenek. Célom egy olyan új mérési eljárás kifejlesztése, ami megkönnyíti a detektormodulok tesztelését. [1]
A kutatóhely rövid bemutatása
A BME Atomfizika Tanszék Optika Laboratóriuma optikával kapcsolatos fejlesztésekkel foglalkozik ipari partnerekkel együttműködve. Egyik ipari partner a preklinikai és humán orvosi diagnosztikai berendezéseket fejlesztő Mediso kft, amellyel több sikeres fejlesztés zárult le eddig. Jelenleg a SPADnet elnevezésű európai konzorcium keretében folyik a kutatás a fent említett résztvevők mellett több európai egyetemmel és kutatóközponttal.
A kutatás történetének, tágabb kontextusának bemutatása
A PET készülékek működésének alapja, hogy a szervezetbe az elektron antianyag párját, pozitront kibocsátó kontraszt anyagot juttatnak olyan módon, hogy a pozitronkibocsátó anyag kövesse a vizsgálni kívánt folyamat térbeli lefutását (1. ábra). A pozitronkibocsátás helyét onnan lehet azonosítani, hogy az antianyag anyaggal való találkozás hatására megsemmisül, és egy egyenes mentén mindkét irányban, azonos időpillanatban két jól meghatározott energiájú gamma-fotont bocsát ki. Ezeket a fotonokat detektálva, elnyelődésük helyét meghatározva és időbeli megjelenésük szerint párba állítva őket lehetőség nyílik az említett egyenesek térbeli elhelyezkedésének meghatározására. Ilyen egyenes-sokaságból egy speciális matematikai transzformáció (Radon transzformáció) segítségével a kontrasztanyag térbeli eloszlása meghatározható.
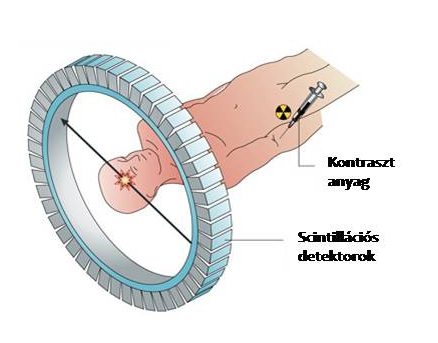
1. Ábra A pozitronemissziós tomográfia alapötlete
A hagyományos detektormodulok gamma-foton elnyelésére néhány 1000 fotonnal válaszoló szcintillátorkristályból készült tűmátrixból, fotoelektron-sokszorozó csövekből (PMT) és a fény kristálytűből való kicsatolását segítő egyéb optikai elemekből állnak. Mivel a fotoelektron-sokszorozó az MRI mágneses terében nem képes megfelelően működni, az új PET/MRI berendezések számára a gyártók új, szilíciumtechnológián alapuló fotoelektron-sokszorozók (SiPM) fejlesztésébe fogtak. [2, 3] Ezek az új érzékelők számos egyéb előnnyel rendelkeznek, így például lehetővé teszik a szcintillátor kristálymátrix folytonos kristálytömbbel való kiváltását, amivel olcsóbb és egyben pontosabb pozíciómeghatározás valósítható meg. Az ilyen detektormodulok tesztelésénél és kísérleti vizsgálatánál azonban nem, vagy csak nehézkesen használható az eddig megszokott méréstechnika.
A kutatás célja, a megválaszolandó kérdések
Feladatom egy olyan mérési eljárás kidolgozása, amely alkalmas az új, szilícium alapú, folytonos szcintillátor kristállyal ellátott detektormodulok vizsgálatára. A hagyományos vizsgálati módszer azon alapul, hogy gamma-foton nyalábbal gerjesztik a szcintillátor tűmátrix egyes elemeit. Tekintve, hogy a gamma-fotonok egy nyaláb mentén haladnak a kristályban, azt egy véges vastagságú vonal mentén gerjesztik (2. ábra). Másképpen megfogalmazva, nem lehet pontosan tudni, hogy a mérés során a gamma-foton a kristálytűben milyen mélységben nyelődött el, vagyis nem lehet tudni, hogy pontosan milyen pontban történt gerjesztésre adott választ mérjük. Ez kristálytűk esetében mégsem jelent gondot, mivel tű a kibocsátott optikai fotonok számára úgynevezett homogenizáló rúdként viselkedik. Vagyis ha szemünk képes lenne ilyen alacsony intenzitású felvillanást látni, akkor sem látnánk pontszerű forrást a kristályban, mindössze azt figyelhetnénk meg, hogy a tű vége világít. Ennek megfelelően azt lehet megállapítani, hogy kristálytűben a felvillanás mélységi információja elvész.
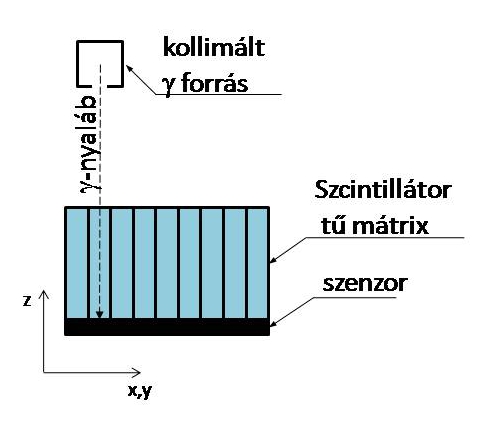
2. Ábra Hagyományos PET modul tesztelési eljárása
Ami szerencse a mérési eljárásban, szerencsétlenség magában az alkalmazásban. A mélységi információ elvesztése úgynevezett parallaxis hibát okoz a gamma-fotonok haladási irányának meghatározásában. (3. ábra) Hiszen, ha az ábrán látható módon a pozitron-kibocsátás a PET készülék látómezejének szélén keletkezik, akkor az egyenes nem közel tengelyirányban hatol be a tűbe, hanem jóval nagyobb szögben. Ez azt jelenti, hogy több kristálytűn is áthaladhat, mire elnyelődik ami a mélységi információ hiányában megnöveli az egyenes detektálásának pontatlanságát.
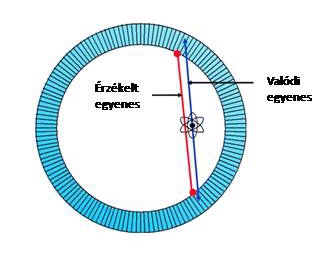
3. Ábra A parallaxis hiba hatása a gamma-foton kibocsátási irányának meghatározására
Folytonos szcintillátorokkal felszerelt detektormodulokban a fényérzékelő síkjában kialakuló fényeloszlás nem független az elnyelés mélységétől. Legegyszerűbb esetben az úgynevezett totálreflexió jelensége miatt csak a szenzorhoz képest adott szögtartományból érkező fény képes kijutni a kristályból. A kialakuló fényfolt mérete ilyenkor függ a szenzortól mért távolságtól. Ebben az esetben a korábban vázolt mérési eljárás nem alkalmazható. Ezért szükség van egy olyan eljárásra, amely pontszerű gerjesztést képes létrehozni a kristályon belül, hiszen bizonyítanunk kell, hogy feltevésünk bonyolultabb optikai elemekkel ellátott detektormodulokban is igaz. Vagyis, hogy a gerjesztés mélységével változik a fényeloszlás. Emellett azt is tudnunk kell, hogy mely fényeloszlás-paraméter mérésével (átmérő, maximális intenzitás, stb.) tudunk következtetni az elnyelődés mélységére.
Módszerek
A gamma-fotonok terjedésének fizikai törvényszerűségeit számba véve arra a következtetésre jutottunk, hogy kontrolláltan pontszerű gerjesztés ilyen módon nem valósítható meg. Nincs olyan eljárás, amivel irányítani lehetne az elnyelődés mélységét. Ennek megfelelően a kristályt valamilyen alternatív módon kell gerjeszteni, emulálni kell a szcintillátor kristályban történő elnyelésre adott választ. Az emuláció kidolgozása folyamán számos dolgot figyelembe kell vennünk. Egyrészt az emulált fényfelvillanásban keletkező fotonok hullámhosszának hasonló eloszlást kell mutatnia, mint a valódi esetben, és ez érvényes a kibocsátott fotonok számára is. A felvillanásnak természetesen pontszerűnek kell lennie, vagy legalább is megfelelően kis térfogatban (0,1mm-nél kisebb átmérőjű gömbben) kell lezajlania. A folyamat időbelisége is fontos: egy valódi felvillanás 100-200 ns hosszúságú, amit az emulált esetben is biztosítani kell.
A közelmúltban bebizonyították, hogy a legelterjedtebb szcintillátor anyag, a LYSO:Ce szcintillátor hasonló hullámhossz-eloszlású fényt bocsát ki ultraibolya (UV) fénnyel történő gerjesztés hatására, mint gamma-fotonra [4]. Eljárásunkat erre a tényre építjük. Az ötlet lényege, hogy egy szcintillátor-üveg szendvicset hozunk létre, amelynek egyik felét olyan, UV fényt átengedő üvegből készítjük el, amely minden egyéb optikai tulajdonságában egyezik a LYSO:Ce kristályéval. Másik fele viszont a szcintillátor kristály. Ha egy ilyen szendvicsbe az üveg felől UV fényt fókuszálunk úgy, hogy a fókuszpont a LYSO:Ce és üveg határrétegre esik, akkor ezen a határfelületen pontszerű gerjesztést kapunk. (4. ábra) Mivel a két anyag optikai tulajdonságai azonosak, a kibocsátott látható fotonok úgy fognak terjedni a szendvicsben, mintha folytonos anyagban haladnának.
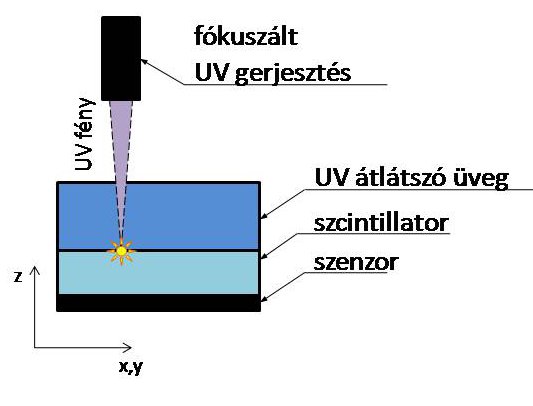
4. ábra Az általunk javasolt mérési elrendezés emulált, folytonos detektormodullal
Ennek az elrendezésnek a kísérleti megvalósításához elengedhetetlen, hogy a gerjesztő fény ne jusson át a kristályon, hiszen ez a fényérzékelőre jutva meghamisítaná a mérést. Ezért elsőként olyan gerjesztő fényforrást kellett találnunk, ami a LYSO:Ce kristályban teljesen elnyelődik. Ehhez megvizsgáltuk a szcintillátoron átjutó fény hullámhosszfüggését, aminek alapján egy 365nm-en sugárzó LED fényforrásra esett a választásunk. Erre alapozva elkészült a megvilágító objektív, amely képes a követelményeknek megfelelően kis méretű gerjesztő foltot létrehozni. A kész optikai elrendezéssel teszteltük, hogy a fény valóban átjut-e a kristályon. A tapasztalat azt mutatta, hogy a LED fényének a teljes intenzitásához képest csekély, a gerjesztett fénnyel viszont összemérhető része halad át a kristályon. A LED spektrumának ezt a nem kívánt részét egy szűrővel zártuk ki. Annak érdekében, hogy az emuláció időbelisége is helyes legyen, a LED-del 100-150 ns hosszú fényimpulzusokat generálunk. Az impulzusok alakját és hosszát szintén kísérletileg ellenőriztük. Az eljárás működőképességének bizonyítására megépített kísérleti elrendezést láthatjuk az alábbi ábrán. Fényérzékelő szenzorként a SensL SPM Array2 fotonszámlálót használtuk.
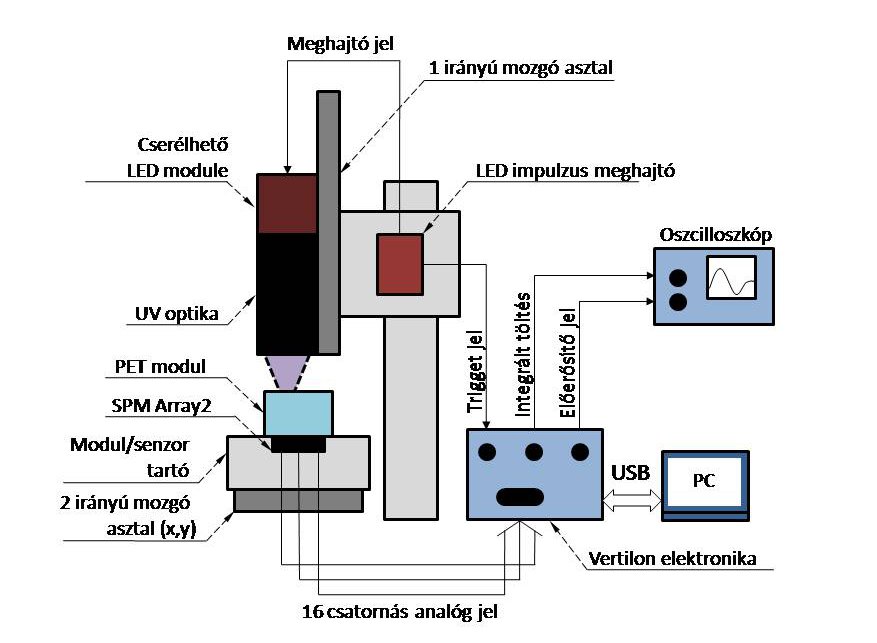
5. ábra Az elkészült kísérleti elrendezés vázlata
Eddigi eredmények
Az eljárás működőképességének bizonyítását három lépésben végeztük. Először megvizsgáltuk, hogy az emulált, szendvics szerkezetű kristálytömbben alkalmazott üveg optikai tulajdonságai valóban egyeznek-e az LYSO:Ce kristályéval. Ezt az összehasonlítást részben irodalmi adatokra támaszkodva, részben saját mérésekkel igazoltuk. [5, S1] Ellenőriztük, hogy a kiválasztott Schott N-LASF44 típusú üveg átengedi-e a LED gerjesztő hullámhosszát (6. ábra). Ezekkel és az előző fejezetben a megvilágításra vonatkozó tesztekkel igazoltuk, hogy sikerült olyan anyagokat és technikai megoldásokat alkalmazni, amelyek lehetővé teszik egy ilyen mérés kivitelezését.
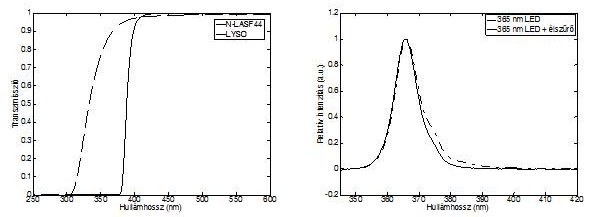
6. ábra Balra a kiválasztott üveg anyag és a LYSO áteresztése a hullámhossz függvényében. Jobbra a gerjesztő fény hullámhossz-eloszlása szűrővel és anélkül.
Második lépésben a kiválasztott SPM Array2-es tulajdonságait vizsgáltuk. Tudnunk kell ugyanis, hogy ennek a 4x4 db pixelből álló szenzornak minden pixele azonos választ ad-e azonos fényintenzitásra, illetve amennyiben nem, milyen korrekciós tényezőt kell figyelembe vennünk. Elképzelhető, hogy ezeknek a szenzoroknak a válasza nem lineárisan függ a bejövő fényintenzitástól, hanem valamilyen függvény szerint. Ezt a detektor nem-linearitást is ellenőriztük a korrekciós tényezők pontos megállapítása érdekében. A szenzorral kapcsolatos méréseink sajnos azt mutatták, hogy a pixelek válasza nagy mértékben eltérő. Nem lehetséges adott beállítás mellett összefüggő fényeloszlást mérni velük. Mivel némelyik pixel csak saját zaját mutatja, míg mások már érzékelési küszöbük felső határát túllépve telítésben vannak (7. ábra), ezért úgy döntöttünk, hogy a szenzor egyik általunk legjobbnak ítélt pixelét használva fogunk méréseket végezni. Először ezt pixelenként a szcintillátor különböző részei alá helyezve mérünk, majd a teljes fényeloszlást ezekből az egyedi mérésekből mozaikként rakjuk össze. Ennek az eljárásnak megvan az az előnye is, hogy tetszőleges méretű fényérzékelőt felépíthetünk. Hátránya természetesen a hosszabb mérési idő.
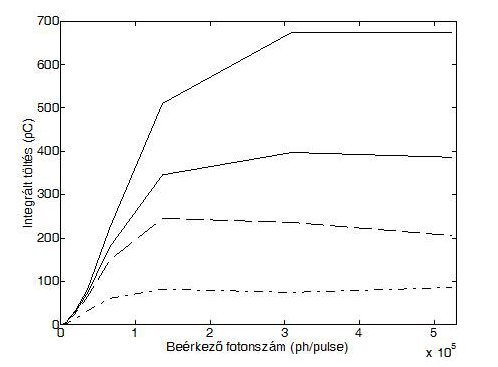
7. ábra Néhány jellemző pixel érzékenységi görbéje a megvilágítás függvényében.
Mindezek ismeretében elkészítettünk egy 10x10x20mm3 detektor modult, amelynek széleit fényelnyelő anyaggal vontuk be (8. ábra). A modult két mélységben lehet gerjeszteni: 3 és 6 mm-re a szenzor felületétől. A kristályt 3x6 elemből álló pixelmátrixszal fedtük le. Egy ilyen elrendezésben csak a korábban említett totálreflexió jelensége határozza meg, hogy mekkora foltméret látható a szenzoron. (9. ábra) Ahogy a korábbiakban megjegyeztem, a foltméret függ a felvillanás kristálybeli mélységétől. Ez a foltméret elméleti úton is jól számolható. A két értéket összevetve pedig mindkét mélység esetén jó egyezést kaptunk. Ezzel a méréssel igazolva láttuk, hogy a rögzített fényeloszlás valóban egy, az emulált kristály belsejében létrejött, felvillanásból származik. [S2]

8. ábra Elkészült emulált kristálymodul, középen gerjesztve
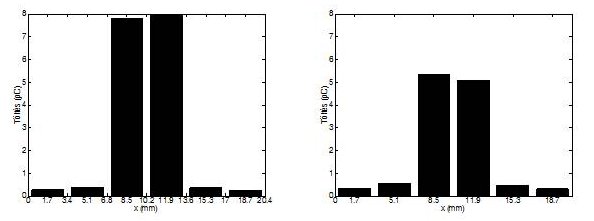
9. ábra A középső pixelsoron mért intenzitásértékek 3 (bal) és 6 mm-re (jobb) a szenzor felületétől.
Várható impakt, további kutatás
Ahhoz hogy az eljárás teljes legyen, még egy lépés hátra van. Meg kell határozni, hogy adott bejövő UV teljesítményre mennyi fotonnal válaszol a kristály. Ennek hiányában abszolút mérést nem, csak összehasonlító jellegűt végezhetünk.
Az elkészült elrendezéssel remélhetőleg a jövőben bármilyen SiPM érzékelőre épülő detektort könnyedén meg tudunk vizsgálni. Egy ilyen vizsgálatnak több eredménye lehet. Használható arra, hogy fényhozam-becslést adjon a különböző detektorkonstrukciók esetén, illetve megjósolja az adott elrendezéssel elérhető térbeli felbontást. Emellett szolgálhat köztes lépésként is. Kis területen sok pixelt (50-100 pixel/cm2) tartalmazó szenzoroknál különös jelentősége van annak, hogy milyen számítási módszerrel határozzuk meg (rekonstruáljuk) a felvillanás eredeti helyét. Ilyen algoritmusok fejlesztőinek a felvillanás helyéhez tartozó nagy mennyiségű valódi fényeloszlás mérés nagy segítséget nyújt eljárásuk finomításához.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája.
[S1] G. Erdei, et al., "Refractive index measurement of cerium-doped Lux-Y2-xSiO5 single crystal," Optical Materials, Vol. 34., Issue 5, 2012, pp.781-785.
[S2] B. Játékos, et al., "Characterization of MRI-compatible PET detector modules by optical excitation of the scintillator material," SPIE Photonics Europe, 2012.
Linkgyűjtemény.
BME, Atomfizika Tanszék, Orvosi képalkotással kapcsolatos fejlesztések
Hivatkozások listája.
[1] Zaidi H. "Recent developments and future trends in nuclear medicine instrumentation", Z Med Phys, 2006;16(1):5-17.
[2] P. Eckert, W. Shen, R. Stamen, and A. Tadday, “Characterisation Studies of Silicon Photomultipliers,” IEEE Jurnal of Quantum Electronics, vol. 44., No. 2., Febr. 2008, pp. 1-11.
[3] N. Dinu, “Electro-optical characterization of SiPM: A comparative study,” Nuclear Instruments and Methods in Physics Research Section A, vol. 610, Oct. 2009, pp. 423-426.
[4] L. Zhang, “Emission Spectra of LSO and LYSO Crystals,” IEEE Nuclear Science Symposium Conference Record, 2007.
[5] Schott AG., "Optical Glass Chatalogue - Description of properties", online, 2011.
