 |
BMe Kutatói pályázat |

|
Fizikai Tudományok Doktori Iskola
BME TTK, Atomfizika Tanszék/Fizika Intézet
Témavezető: Dr. Gali Ádám
Félvezető nanokristályok biológiai nyomjelző és napelem alkalmazásokhoz
A kutatási téma néhány soros bemutatása
Kutatásaim biológiai nyomjelző és harmadik generációs napelem alkalmazásokhoz használt, negyedik főcsoportbeli félvezető, nanométer méterű kristályok (nanokristályok) optikai tulajdonságainak megismerésére irányulnak. Munkám elméleti jellegű, a nanokristályok optikai tulajdonságait első elvekből levezetett egyenletek segítségével szimulálom szuperszámítógépeken. A számolások segítségével korábbi kísérleti eredmények megértéséhez járultam hozzá, illetve kísérletileg még nem ismert jelenségek vizsgálatára adtam ötleteket.
A kutatóhely rövid bemutatása
Munkámat Dr. Gali Ádám kutatócsoportjában végzem az Atomfizika Tanszéken. Számításaink kis részét a helyi számítógépes klaszterünkön végezzük, a produkciós futások a nagy számítási igény miatt javarészt nemzetközi együttműködéseken keresztül, külföldi szuperszámítógépeken történnek.
A kutatás történetének, tágabb kontextusának bemutatása
Az utóbbi évtized kísérleti technikáinak fejlődésének hála a nanométer méretű kristályokat is sok esetben rutinszerűen lehet előállítani. Bizonyos kivételes esetekben ez atomi pontosságú szabályozást jelent. Az ilyen nanométer mérettartományba eső nanokristályok speciális tulajdonságokkal rendelkezhetnek a makroméretű, makroszkopikus kristályokhoz képest. Ilyen például, hogy a tömbi méretekben fotolumineszcens tulajdonságokkal nem rendelkező anyag nanoméretben jelentős fotolumineszcencia jelet adhat. Az is nagyon érdekes, hogy az ilyen nanokristályok színe a mérettel hangolható. Mindezen jelenségek egy alapvető kvantummechanikai effektussal, az ún. kvantum bezártsággal magyarázhatók.
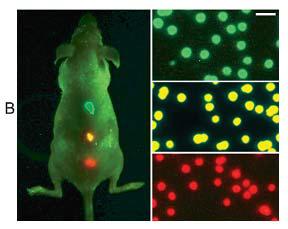
Balra: élő egérben nanokristályokkal megvalósított optikailag detektált biológiai nyomkövetés, jobbra: a nanokristály színe a nanokristály méretével hangolható [1].
Mivel ilyen méretekben drasztikusan megváltozik a felület/térfogat arány a makroszkopikus (mm-cm) méterű kristályokhoz képest, a felület különös jelentőséggel bír és nagyon sok esetben az határozza meg a kristály tulajdonságait, felülírva az egyszerű kvantum bezártságból adódó várakozásokat. Az, hogy a felület ennyire fontos valamilyen szempontból hátrány, hiszen nagyon körültekintőnek kell lenni az anyagok előállításával, kezelésével, ugyanakkor előny is, mivel jól kiforrott kémiai módszerekkel lehet befolyásolni a felületi atomok, funkciós csoportok helyzetét, amivel a nanokristályok tulajdonságát a megfelelő irányba lehet hangolni.

Kadmium-szulfid (CdS) nanokristályok felhasználásával készült napelem festék [2]. A festék színe a nanokristályok méretével szabályozható.
Felhasználva a nanokristályok kis méretét és hangolható színét, felmerül a gondolat, hogy optikailag detektált nyomkövetést valósítsunk meg az emberi szervezetben [1]. A mérettel való fényelnyelési tulajdonságok miatt természetesen merül fel az az ötlet is, hogy a nanokristályokat napelemek aktív fényelnyelő elemeként lehetne használni teljesen lefedve a nap sugárzási spektrumát [2,3].
A kutatás célja, a megválaszolandó kérdések.
Kutatásaimnak, amelyet a „számítógépes anyagtudomány” területbe sorolok, két fő célja van. Egyrészt szeretném elősegíteni a már rendelkezésre álló kísérleti eredmények megértését, másrészt szeretnék olyan jóslatokat tenni, amelyekkel le lehet csökkenteni a kísérletezésre szánt emberi és pénzügyi forrásokat, mivel a szimulációk sok esetben gyorsabbak és gyakorlatilag minden esetben olcsóbbak is.
Az utóbbi évek során elvégzett munkám két fő alterületre osztható: főleg a periódusos rendszer negyedik főcsoportjában található elemekből felépülő, gyémánt és szilícium nanokristályokkal foglalkoztam.
Gyémánt nanokristályok
Kísérleti áttörés volt, hogy 99%-os tisztaságú speciális gyémánt nanokristályokat, ún. diamondoid-okat állítottak elő [4]. Ezek atomi szerkezete teljes mértékben ismert a szerves vegyületekhez hasonlóan. Ez ritkaságnak számít a nanorendszerek fizikájában, úgyhogy ideális keretet nyújtanak arra, hogy a különböző kísérleti/számítási módszereket teszteljük. Mivel nagy pontosságú mérési adatok álltak rendelkezésre az optikai tulajdonságukat illetően [4], feladatul tűztem ki, hogy ezeket megvizsgáljam atomi szimulációkkal.
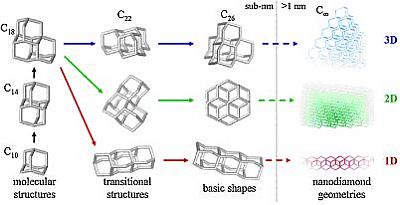
Gyémánt nanokristályok szerkezeti ábrája, a szürke vonalak kovalens szén-szén kötéseket jelölnek. Megfigyelhető, hogy a tömbi gyémánthoz hasonlóan a nanokristályokban is tetraéderes szén-szén kötések vannak, emiatt stabilitásuk is hasonló. A legkisebb gyémánt nanokristály a C10-el jelölt bal alsó struktúra, az adamantane.
Szilícium nanokristályok
Arthur Nozik, az amerikai NREL intézet munkatársa az újfajta, ún. harmadik generációs napelemek élharcosa [5,6]. Nozik 2002-ben publikált cikke nagy feltűnést keltett [7], melyben először vetette fel, hogy miért lenne igazán előnyös nanokristályokat használni napelemekben, amelyek az olcsóbb és hatékonyabb napelemek előfutárai lehetnének: az ún. Multiple Exciton Generation (MEG) folyamatnál több lyuk-elektron pár kinyerésére is van lehetőség egy beeső fotonra, ami növelné a napelem hatásfokát. Munkám során megvizsgáltam, hogy az ilyen célú felhasználás esetén fontos tulajdonságok hogyan változnak meg a napelemipar legfontosabb alapanyagából, a szilíciumból készült nanokristályok esetén [8].
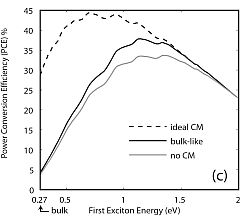
Olyan napelemek maximális elméleti hatásfoka, amelyek kihasználják a MEG effektust [9]. A legjobb ilyen napelem elérhetné a 44%-os hatásfokot is. Összehasonlításképpen az elméleti maximum egykristályos szilícium napelemeknél kb. 32% [5].

Az első olyan laborban előállított ólom-szelenid (PbSe) nanokristály alapú napelemstruktúra hamis színezésű keresztmetszeti ábrája, melyben 100%-nál nagyobb belső kvantumhatásfokot mértek, ami a MEG effektus egyértelmű kísérleti bizonyítéka. Az eszköz külső (teljes) hatásfoka a 4%-ot is elérte [10].
Módszerek
Atomi szintű modellezés
Mivel az atomi mérettartományban az elektronok hullámviselkedése egyáltalán nem elhanyagolható, atomi szintű szimulációk szükségesek. Sajnos az ezt a viselkedést leíró Schrödinger-egyenlet numerikus megoldása csak kisszámú elektron esetén létezik, így további módszereket kell segítségül hívni. Munkám során sűrűségfunkcionál-elmélet alapú módszereket használtam, amik azon alapulnak, hogy a nagyon komplex teljes hullámfüggvény helyett csak az elektronok sűrűséget kezelik. Noha ez elvileg egzakt eljárás, a gyakorlatban komoly közelítéseket kell alkalmazni. Ezek a számolások a rendszer külső elektromos tér-mentes alapállapotát adják meg, a fénnyel való kölcsönhatás kiszámításához további módszerek szükségesek: ehhez az időfüggő sűrűségfunkcionál-elméletet hívtam segítségül, amellyel számolható a rendszer abszorpciós tulajdonsága. A napelemes alkalmazásnál pedig az elektronok dinamikájára vagyunk kíváncsiak, amelynek vizsgálatára egy perturbációs eljárást vezettem le és fejlesztettem ki egy már elérhető programcsomagban. Ebben az esetben azt számoltam ki, hogy mi a fény által gerjesztett lyuk-elektron párok lebomlásának az időegységre jutó átmeneti valószínűsége.
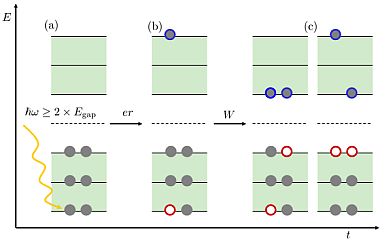
A MEG effektus impakt ionizációs modelljének időbeli lefolyása. (a) Amennyiben egy elegendően nagy energiájú foton (sárga hullámos vonal) érkezik a mintára, (b) az elnyelődés hatására létrejött ún. forró töltéshordozók (c) újabb töltéshordozó párokat kelthetnek. A színes teli (lyukas) körök elektronokat (lyukakat) jelképeznek. Minél magasabban (mélyebben) van energiában egy elektron (lyuk), annál nagyobb valószínűséggel kelt újabb lyuk-elektron párokat.
Szuperszámítógépek
Mivel ezek a számolások igen számításigényesek és a rendszer karakterisztikus méretének (N) N3 illetve N4 hatványával skálázódnak, ezért elengedhetetlen, hogy hatékonyan fussanak. Ez a skálázódás egyébként azt jelenti, hogyha megduplázzuk a szimulálni kívánt rendszer méretét, akkor nyolcszorosára (tizenhatszorosára) nő a számításigény. Ilyenkor egy-egy számolás időigénye annyira megnő, hogy az optimális futás elengedhetetlen. A hatékony futtatáshoz alapvetően két módszer van: (1) optimalizáljuk a megoldásra használt algoritmust, (2) felkészítjük a programot egyszerre több processzor használatára. Én általában a második részre helyeztem több hangsúlyt, a legnagyobb szimulációknál egyszerre 128-256 processzort (tipikusan kettő hatványai szerint szokták felosztani a folyamatokat) használtam akár több hetes futásidővel sokszor terabájtos memória igénnyel.

A Wigner Fizikai Kutatóközpontban található szuperszámítógép: egy rack szekrény, amelyben a lapos egységek az egyes számítógépek. Az összeköttetésért a lentebb látható kisebb modul, egy infiniband switch a felelős.
Eddigi eredmények
Gyémánt nanokristályok
Gyémánt nanokristályokat vizsgálva megállapítottam, hogy az időfüggő sűrűségfunkcionál-elmélet segítségével kiszámolt abszorpciós spektrumok egyrészt a kísérletivel nagyon jó egyezést mutattak, másrészt megmutattam, hogy ún. Rydberg átmenetek uralják a spektrum alacsonyenergiás részét még viszonylag nagy nanokristályoknál is [V1,V2]. A Rydberg átmenetek nagyon jól ismertek szerves molekuláknál, de félvezető nanokristályoknál tudtommal még nem tapasztaltak ilyet. Ez a szokatlan tulajdonság magyarázhatja például a nanogyémánt jó elektron-emitter tulajdonságát [11]. Mivel ezen Rydberg állapotok kiterjedése igen nagy, jelentősen túlnyúlik a nanokristályokon, ezért szenzoros alkalmazásokban is érdekes lehet.
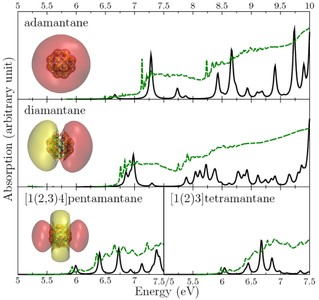
Néhány kiválasztott gyémánt nanokristály kísérleti (zöld szaggatott vonal) és elméleti (fekete folytonos vonal) abszorpciós spektruma [V1,V2]. A piros-sárga ábrák fentről lefele rendre s, p, d típusú Rydberg pályákat jelölnek.
Megvizsgáltam azt is, hogy mi történik akkor, ha ezeket a nanokristályok felületét célzottan megváltoztatjuk. Azt találtam, hogy kettős kötésű kén atomokat helyezve a nanokristály felszínére, az optikai gap az ultraibolya tartományból a látható/infravörös tartományba esik le, ezáltal esetleg – a nanogyémánt megfelelő mérete és nem toxikus tulajdonsága miatt is – biomarker alkalmazásokban is használható lehetne a gyémánt, ahol az infravörös lumineszcencia elengedhetetlen követelmény [V2,V3].
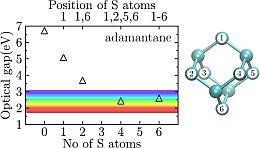
Balra: A legkisebb gyémánt nanokristály, adamantane első optikai gerjesztési energiájának a felületen lévő kén atomok számától való függése. Minél több kén atom van a felületen, annál kisebb az optikai tiltott sáv, négy és hat kén atom esetén már a látható tartományban nyel el az adamantane [V3]. Jobbra: az adamantane szerkezeti ábrája, a türkiz gömbök szén atomokat jelölnek.
Szilícium nanokristályok
A szilícium nanokristályoknál megmutattam, hogy optikai elnyelésük jelentősen függ a nanokristályok alakjától, a felület atomi átrendeződésétől, illetve a felületen lévő funkciós csoporttól [V4]. A kutatást folytatva kifejlesztettem egy kódot, sűrűségfunkcionál-elméletet és perturbációs módszert alkalmazva, amely képes kiszámolni nanokristályokra a MEG folyamat átmeneti valószínűségét az impakt ionizációs közelítésen belül. Azt találtam, hogy a nanokristályok felületi strukturáltsága jelentősen megnöveli az átmeneti valószínűséget [V5]. Ez kedvező üzenet a kísérleti csoportoknak, hiszen ennek segítségével lehet növelni a szükséges folyamat valószínűségét. Ezen eredmények fényében megvizsgáltuk azt is, hogy a tömbi szilícium magas nyomású fázisaiból készített nanokristályok milyen impakt ionizációs tulajdonságokat mutatnak. A várakozásoknak megfelelően nagyon kedvező eredményeket kaptunk, ami leginkább az ilyen fázisok alacsony tiltott sávjának köszönhető [V6].
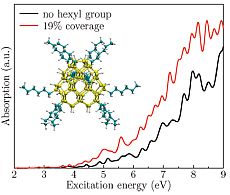
Szilícium nanokristály abszorpciójának a növekedése a hexilcsoportos fedés hatására: piros vonal a hexilcsoportokkal, fekete vonal azok nélkül.
Várható impakt, további kutatás
Doktori munkám során megjelent cikkeimre az írás pillanatáig 22 független hivatkozás érkezett. A szilíciummal kapcsolatos eredményeinkről egy recenzió jelent meg az MRS Bulletin-ban, mindemellett a legújabb Nature cikk hivatkozik rá [11]. Több nemzetközi konferencián előadást tartottam kutatásaimról, a „Time-dependent density Functional Theory: prospects and applications” konferencián bemutatott poszteremet kiválasztották az öt legjobb poszter közé. Mindezeken felül sikerült elnyernem az egyetem számára az elméleti spektroszkópia témakörében jártas fiatal kutatók következő éves konferenciájának, a 2013. évi European Theoretical Spectroscopy Facility Young Researchers’ Meeting rendezési jogát.
A terület annyira szerteágazó, hogy nagyon sok irányban lehet tovább haladni. Az általam felvázolt területeken kívül nagyon érdekes még az ún. színcentrumok vizsgálata. A színcentrumok olyan atomi hibák a kristályban, amelyeket akár szilárdtestalapú kvantumszámítógép létrehozására is lehetne alkalmazni [12]. Nagyon friss kísérleti eredménynek számít, hogy ilyen színcentrumokat nanokristályokban is létre tudtak hozni [13].
Saját publikációk, hivatkozások, linkgyűjtemény
Saját publikációk
[V1] Márton Vörös and Adam Gali, Optical absorption of diamond nanocrystals from ab initio density functional calculations
Physical Review B 80, 161411(R) (2009)
[V2] Márton Vörös, Tamás Demjén, Adam Gali, The Absorption of Diamondoids from Time-dependent Density Functional Calculations
MRS Spring Meeting Proceedings 1370, mrss11-1370-yy02-07 (2011)
[V3] Márton Vörös, Tamás Demjén, Tibor Szilvási, Adam Gali, Tuning the optical gap of nanometer-size diamond cages by sulfurization: A time-dependent density functional study
Physical Review Letters, közlésre elfogadva (2012)
[V4] Adam Gali, Márton Vörös, Dario Rocca, Gergely T. Zimanyi and Giulia
Galli, High Energy Excitations in Silicon Nanoparticles
[V5] Márton Vörös, Dario Rocca, Giulia Galli, Gergely T. Zimanyi and Adam Gali, Increasing the efficiency of Multiple Exciton Generation in Si nanoparticles: an ab-initio study
Physical Review Letters, elbírálás alatt
[V6] Stefan Wippermann, Márton Vörös, Dario Rocca, A. Gali, G. T. Zimanyi and G. Galli, High pressure phase Si nanoparticles: Applications to solar energy conversion
Előkészületben
Egyéb publikációk
[V7] Márton Vörös, Péter Deák, Thomas Frauenheim, Adam Gali, The absorption spectrum of hydrogenated silicon carbide nanocrystals from ab initio calculations
Applied Physics Letters 96, 051909 (2010)
[V8] Márton Vörös, Péter Deák, Thomas Frauenheim, Adam Gali, The absorption of oxygenated silicon carbide nanoparticles
The Journal of Chemical Physics 133, 064705 (2010)
[V9] Márton Vörös, Péter Deák, Thomas Frauenheim, Adam Gali, Time-dependent density functional calculations on hydrogenated silicon carbide nanocrystals
Mater. Sci. Forum 679 - 680, 516 (2011)
[V10] Márton Vörös, Péter Deák, Thomas Frauenheim, Adam Gali, Influence of oxygen on the absorption of silicon carbide nanoparticles
Mater. Sci. Forum 679 - 680, 520 (2011)
[V11] Márton Vörös, Adam Gali, Efthimios Kaxiras, Thomas Frauenheim,
Jan Knaup, Identification of defects at the interface between 3C-SiC quantum dots and a SiO2 embedding matrix
Phys. Status Solidi B 249, 360 (2012)
[V12] Jan Knaup, Márton Vörös, Péter Deák, Adam Gali, Thomas Frauenheim,
Efthimios Kaxiras, Annealing Simulations to Determine the Matrix Interface Structure of SiC Quantum Dots Embedded in SiO2
Phys. Status Solidi C 7, 407 (2010)
Linkgyűjtemény
Dr. Gali Ádám kutatócsoportja:
http://www.fat.bme.hu/kulonc/galia/
Wikipédia oldalak:
http://en.wikipedia.org/wiki/Multiple_exciton_generation
http://en.wikipedia.org/wiki/Nanocrystal
http://en.wikipedia.org/wiki/Third_generation_photovoltaic_cell
UC Davis:
http://physics.ucdavis.edu/zimanyi/
NREL intézet:
Referenciák
[1] Maureen A Walling, Jennifer A Novak, and Jason R. E Shepard, Quantum Dots for Live Cell and In Vivo Imaging
[2] Matthew P. Genovese, Ian V. Lightcap, and Prashant V. Kamat, Sun-Believable Solar Paint. A Transformative One-Step Approach for Designing Nanocrystalline Solar Cells
[3] Illan J. Kramer and Edward H. Sargent, Colloidal Quantum Dot Photovoltaics: A Path Forward
[4] L. Landt, K. Klunder, J. E. Dahl, R. M. K. Carlson, T. Moller, and C. Bostedt, Optical Response of Diamond Nanocrystals as a Function of Particle Size, Shape, and Symmetry
Phys. Rev. Lett. 103, 047402 (2009)
[5] W. Shockley and H. J. Queisser, Detailed Balance Limit of Efficiency of p-n Junction Solar Cells
Journal of Applied Physics 32, 510 (1961)
[6] M. Green, Third generation photovoltaics: advanced solar energy conversion,
Springer series in photonics, Springer, 2006
[7] A. J. Nozik, Quantum Dot Solar Cells
Physica E: Low-dimensional Systems and Nanostructures 14, 115 (2002).
[8] Trinh, M. T., Limpens, R., de Boer, W. D. A. M., Schins, J. M., Siebbeles, L. D. A., and Gregorkiewicz, T., Direct generation of multiple excitons in adjacent silicon nanocrystals revealed by induced absorption
Nature Photonics 6, 316 (2012)
[9] Gautham Nair, Liang-Yi Chang, Scott M. Geyer, and Moungi G. Bawendi, Perspective on the Prospects of a Carrier Multiplication Nanocrystal Solar Cell
[10] Octavi E. Semonin, Joseph M. Luther, Sukgeun Choi, Hsiang-Yu Chen, Jianbo Gao, Arthur J. Nozik, Matthew C. Beard, Peak External Photocurrent Quantum Efficiency Exceeding 100% via MEG in a Quantum Dot Solar Cell
[11] Trinh, M. T., Limpens, R., de Boer, W. D. A. M., Schins, J. M., Siebbeles, L. D. A., and Gregorkiewicz, T., Direct generation of multiple excitons in adjacent silicon nanocrystals revealed by induced absorption
Nature Photonics 6, 316 (2012)
[12] L. Yang, és tsai, Monochromatic Electron Photoemission from Diamondoid Monolayers
[13] L. Childress és tsai, Coherent Dynamics of Coupled Electron and Nuclear Spin Qubits in Diamond
[14] Yi-Ren Chang és tsai, Mass production and dynamic imaging of fluorescent nanodiamonds
Nature Nanotechnology 3, 284 (2008)
