 |
BMe Kutatói pályázat |

|
Oláh György Doktori Iskola
BME VBK, Szervetlen és Analitikai Kémia Tanszék
Témavezető: Dr. Veszprémi Tamás
Molekuláris reakcióoptimalizálás nagy térkitöltésű csoportokkal
A kutatási téma néhány soros bemutatása
Munkám során nagy térkitöltésű csoportok kémiai reakciókra gyakorolt speciális hatásait vizsgálom elméleti módszerekkel. Kutatási eredményeim új megközelítést adnak eddig ismeretlen kémiai reakciók megtervezésére, illetve a már ismert reakciók optimálására.
A kutatóhely rövid bemutatása
A Szervetlen és Analitikai Kémia Tanszéken immár évtizedes hagyománya van a különleges elektronszerkezetű vegyületek elméleti kémiai vizsgálatának, különös tekintettel az alacsony koordinációjú szén és szilícium vegyületekre. A Tanszék számos nemzetközi együttműködése és a témában megjelent kiemelkedően magas színvonalú publikációi jól jellemzik a kutatások elismertségét.
A kutatás történetének, tágabb kontextusának bemutatása
Évszázados tapasztalat, hogy kémiai reakciók lelassíthatók, sőt akár meg is szüntethetők, ha nagyméretű inert csoportok vannak a reakciócentrumok közelében. Ekkor a sztérikus vagy más néven nagy térkitöltésű csoportok egyszerűen meggátolják, hogy a két reakciópartner megközelíthesse egymást és ezáltal blokkolják a reakciót (1. ábra). Ez az elv alapvetőnek bizonyult reaktív rendszerek előállításakor, ahol kifejezetten kedvező a reakció hiánya, így az elmúlt évtizedekben több rendkívül meglepő eredmény született
.
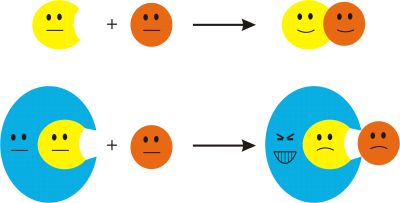
1. ábra. Sztérikus csoportok hatása
Ilyen volt a kettős kötés szabály megcáfolása. A kettős kötés szabály szerint csak szén, nitrogén és oxigén képes többszörös kötés kialakítására. A kémikusok más elemek között túl gyengének, és ezért nagyon reaktívnak tartották a kettős kötést, így tartós létezését elvetették. Emiatt volt alapvető az első stabil Si = Si kettős kötést tartalmazó vegyület előállítása [1, 2], melyet több meglepő felismerés követett [3, 4, 5].
Hasonló hatást váltott ki az első divalens szén- és szilíciumvegyület (karbén, szililén) előállítása [6, 7]. A szén és a szilícium is négy kémiai kötést alakít ki vegyületeiben. A periódusos rendszerben elfoglalt helyük alapján azonban két kötés kialakulása is elképzelhető lenne. Erre sikerült példát mutatni, sőt nemrég egy formálisan nulla kötést kialakító szénvegyületet mutattak be [8].
A kémiai kíváncsiságon felül komoly lendületet adott a terület kutatásának az a felismerés, hogy ezek a vegyületek kitűnő katalizátorok. Egyes karbén-családok jobban aktiválják a hidrogént, mint a platina [9]. Ennek eredményeként több hagyományos átmenetifém katalizátoros reakciót sikerülhet lecserélni környezetbarát technológiára. Éppen ezért a divalens szén- és szilíciumvegyületek reakcióinak tanulmányozása és mélyebb megértése elengedhetetlen. A helyzetet jól jellemzi, hogy a Web of Science szerint karbénekről közel ugyanannyi közlemény jelent meg, mint a grafénnel kapcsolatban.
A kutatás célja, a megválaszolandó kérdések.
Mint láttuk, a nagy térkitöltésű csoportok meghatározó szerepet játszanak a reaktív vegyületek stabilitásában, mivel megakadályozzák a gyors elreagálásukat. Ugyanezen ok miatt fontosak a megvalósítani kívánt reakciók szempontjából is. Elméleti kutatások eddig nem foglalkoztak valódi, a kísérletekben alkalmazott szubsztituensek hatásának vizsgálatával, mivel számítástechnikailag kivitelezhetetlenek voltak ilyen szimulációk. Emiatt modellvegyületeket szokás alkalmazni, ahol a nagy térkitöltésű csoportokat például egy hidrogénatommal helyettesítik, így hatásukat elhanyagolják. A nagy teljesítményű számítógépeknek és az elmélet fejlődésének hála mára azonban elérhetővé vált valódi rendszerek teljes szimulációja.
Munkám során olyan reakciók vizsgálatára fókuszáltam, amelyeket a modellvegyületek képtelenek voltak megmagyarázni. Az irodalomban számos olyan anomális reakciót is találtam, amelyek arra utaltak, hogy a nagy térkitöltésű csoportoknak a jól ismert reakciógátló tulajdonságukon túl más eltérő hatásuk is lehet. Feladatom volt ezen anomáliák feloldása és a nagy térkitöltésű csoportok különleges tulajdonságainak mélyebb megértése, és elméletük kiegészítése. Eddigi munkám két témakör köré csoportosítható.
A kettős kötés szabály megcáfolása után ugyanazzal a reakciósémával több meglepő szerkezetű vegyületet is előállítottak nagy kitermeléssel, csupán a nagy térkitöltésű csoportok változtatásával [10, 11, 12, 13]. A modellvegyületeken végzett számítások szerint számos energetikailag hasonló szerkezet lehetséges, így felmerül a kérdés, hogy miként lehet a nagy térkitöltésű csoportoknak rendkívül precíz és szelektív irányító hatása.
A fehér foszfor (P4) fontos kiinduló vegyülete számos növényvédő- és rovarirtószernek. A jelenlegi technológiák a P4 aktiválását drága és mérgező nehézfém komplexek segítségével oldják meg, melynek kiváltása költség- és környezetkímélő lenne. A P4 reakciója többféle karbénnel is ismert [14, 15, 16], míg szililének esetén mindössze egyetlen eggyel [17], aminek az okát egyelőre nem sikerült megmagyarázni.
Módszerek
Munkám során a legmodernebb elméleti kémiai és fizikai elméleteket alkalmazom (ab initio, post-HF módszerek, sűrűségfunkcionál elmélet, QTAIM) nagy teljesítményű számítógépeket felhasználva. Központi kérdés a klasszikus kémiai fogalmak, többek között a kémiai kötés, stabil molekula, kémiai reakció stb. megfeleltetése a modern fizikai elméletek eszköztárának.
Ennek egyik legfontosabb eleme az ún. potenciális energia hiperfelület (PES), mely a Schrödinger-egyenletből a Born-Oppenheimer közelítéssel származtatható. E szerint a különböző atommag-konfigurációkhoz egy-egy energiaérték rendelhető, ami egy 3N-6 dimenziós felületet ad (ahol N az atommagok száma). A kémiai átalakulások ezen a felületen való mozgásnak feleltethetők meg. A PES egydimenziós speciális metszetei a kémikusok számára jól ismert reakciókoordináta fogalmával kapcsolhatók össze (2. ábra). A reakciókoordináta (q) olyan geometriai paraméter, amely méri a reakció előrehaladását. A görbe maximuma az átmeneti állapot, amely megadja, hogy a reakció lejátszódásához mekkora energiagátat kell leküzdeni.
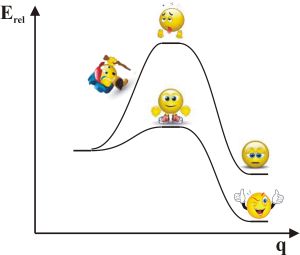
2. ábra. A reakciókoordináta
Ezt az értéket a reakciókinetika átmeneti állapot elmélete összekapcsolja a reakciók sebességével. A potenciális energia hiperfelületen az átmeneti állapot megfeleltethető két völgy közötti hágónak, vagyis egy nyeregpontnak. A reakciómechanizmus felderítésekor a szimulációink legfőképp e nyeregpontok megtalálására összpontosulnak. A probléma nehézségét az adja, hogy mind a mai napig nem ismert egyértelmű algoritmus a megtalálására. Emiatt különféle közelítő módszerek, komoly kémiai intuíció és tapasztalat mellett jó adag szerencsére is szükség van a nyeregpontok belátható időn belüli megtalálásához.
A nagy térkitöltésű csoportok klasszikus elmélete is jól megjeleníthető az egydimenziós metszeteken (2. ábra): a sztérikus csoportok hatására az aktiválási energiagát megnő, lecsökkentve ezzel a reakciósebességet.
Eddigi eredmények
Reaktív szilíciumvegyületek előállítása
Sikerült kimutatni, hogy a nagy térkitöltésű csoportoknak a reakció menetét irányító hatását nem a megnövekedett aktiválási gátak okozzák, hanem a potenciálfelület alakjának megváltozása (3. ábra) [T1]. A kísérletekben alkalmazott csoportok destabilizálták az összes kompetitív szerkezetet, vagyis megszűntek bizonyos minimumok a potenciálfelületen, és így gyakorlatilag csak egy reakciócsatorna maradt nyitva, ami a végtermékhez vezetett. Ráadásul a végtermék esetén a szubsztituensek tökéletes fedést nyújtottak, és így megakadályozták a reaktív szerkezet elbomlását.
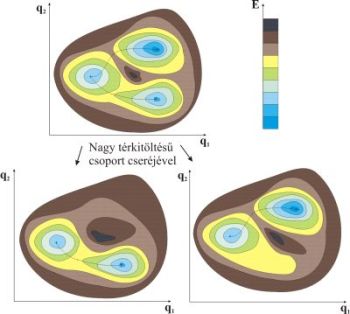
3. ábra. A sztérikus csoport lehetséges hatása a reakcióra
Az eredményeket felhasználva sikerült megfelelő nagy térkitöltésű csoportot tervezni a hexaszilabenzol előállításához (4. ábra), melyet a szilíciumkémia szent gráljának tekintenek. A kísérleti munkát két kutatócsoport (Prof. West, University of Wisconsin és Prof. Tamao, RIKEN, Japán) is azonnal vállalta.
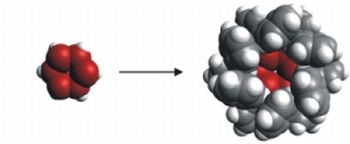
4. ábra. Hexaszilabenzol-tervezés
Fehér foszfor aktiválása szililénekkel
Munkám során megmutattam, hogy modellvegyületek alapján a reakció egyedisége nem magyarázható meg [T2, T3]. A nagy térkitöltésű csoportok vizsgálata azt mutatta [T4], hogy egy szubsztituens meglepő módon csökkenti a sebességmeghatározó aktiválási gátat (éppen a pozitív kísérleti példa sztérikus csoportja), míg a többi csoport a várakozásnak megfelelően megnöveli azt (5. ábra). A szubsztituens tehát ebben az esetben nem gátolja, hanem elősegíti a reakciót, amelyre eddig még soha nem mutattak példát.
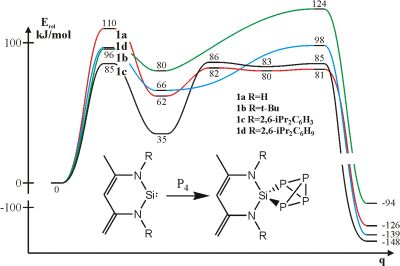
5. ábra. Fehér foszfor aktiválása szililénnel
Az ellentmondás feloldása a kedvező másodlagos kölcsönhatásokban rejlik, mely a molekulák van der Waals reprezentációjában jól látható (6. ábra). Ez alapján az enzimkatalízissel analóg magyarázatot tudtam adni. A különféle nagy térkitöltésű csoportokat tartalmazó szililének esetén a piros nyilak jelölik, hogy a sárga foszforatomok és a szubsztituensek között hol van jelentős átfedés, azaz taszítás.
A pozitív kísérletben alkalmazott szubsztituens (1c) esetén nincs ilyen, a négy foszforatom tökéletesen illik a sztérikus csoportok által létrehozott üregbe, így tehát csak kedvező kölcsönhatás jön létre a szubsztituens és a foszforatomok között.
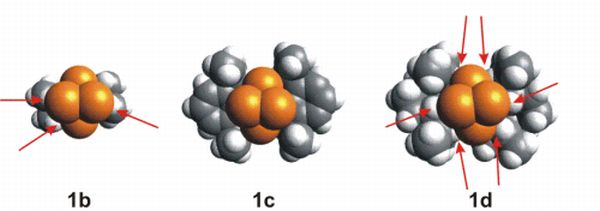
6. ábra. Különböző szubsztituensű szililén Van der Waals reprezentációja. Piros nyilak mutatják a sztérikus taszítást
Hasonló módon fogalmazható meg az enzimek működése, ahol az alakszelektivitásnak és a nemkötő kölcsönhatásoknak szintén fontos szerepük van. Ezzel az eredménnyel a foszfor karbénnel való reakcióját is sikerült értelmezni, ugyanis minden reagáló karbén ugyanezt a nagy térkitöltésű csoportot tartalmazta.
7. ábra. Sztérikus csoportok módosításának elve
Az elv ismeretében (7. ábra) sikerült egy másik szililént tervezni [T5], amelynél az aktiválási gát csökkenése még jelentősebb. A kísérleti preparatív munkát Prof. R. West (University of Wisconsin) és kollégái végezték.
Várható impakt, további kutatás
Munkám során megmutattam, hogy nagy térkitöltésű csoportokkal hogyan lehet szilíciumvegyületek szintézisét szelektíven irányítani, és sebességét akár módosítani is. Ezek az eredmények alapvetően új lehetőségeket nyitnak meg, ezért a tudományterületünk legrangosabb nemzetközi folyóirataiban publikáltuk őket. Konkrét eredményeink általánosan megfogalmazható alapelvekre építenek, ezért kiterjeszthetők a kémia nagy részére. Az elv segítségével és az általunk bemutatott tervezési módszerekkel számos, eleddig meg nem valósított reakció realizálhatóvá válik, mások a kívánalmaknak megfelelően felgyorsíthatók vagy éppen lassíthatók lesznek.
Az eredmények ilyen megfogalmazása nagy visszhangot váltott ki, és ennek eredményeként tavaly megkaptam az Észak-Rajna Vesztfália tartomány által alapított és az egész világra kiterjesztett nagy presztízsű német Fiatal Kutatói Díjat kémiából, melyet magyar, de még kelet-európai sem kapott meg eddig soha semmilyen tudományterületen.
A jövőben eredményeink minél szélesebb körű alkalmazására kívánok koncentrálni [T6].
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
[T1] T. Szilvási, T. Veszprémi: Molecular-tailoring: Reaction path control with bulky substituents, Organometallics, 31, 3207 (2012)
[T2] K. Nyíri, T. Szilvási, T. Veszprémi: The mechanism and energetics of insertion reactions of silylenes, Dalton Trans. 39, 9347 (2010)
[T3] T. Szilvási, K. Nyíri, T. Veszprémi: On the unique insertion mechanisms of β-diketiminato-silylene, Organometallics, 30, 5344 (2011)
[T4] T. Szilvási, T. Veszprémi: On the mechanism of the reaction of white phosphorus with silylenes, Dalton Trans. 40, 7193 (2011)
[T5] T. Szilvási, R. West, T. Veszprémi: Molecular-tailoring: Internal catalytic effect of bulky substituents, publikációra előkészítve
[T6] T. Szilvási, T. Veszprémi: Molecular-tailoring: Internal catalytic effect of bulky NHC ligands in Suzuki-Miyaura coupling: Revised theory of bulky groups, publikációra előkészítve
Hivatkozások listája
[1] R. West, M. J. Fink, J. Michl: Tetramesityldisilene, a stable compound containing a silicon-Silicon double bond, Science, 214, 1343 (1981)
[2] R. West: Isolable Compounds Containing a Silicon-Silicon Double Bond, Science, 225, 4667 (1984)
[3] L. Gagliardi, B. O. Roos: Quantum chemical calculations show that the uranium molecule U2 has a quintuple bond, Nature, 433, 848 (2005)
[4] T. Nguyen, A. D. Sutton, M. Brynda, J. C. Fettinger, G. J. Long, P. P. Power: Synthesis of a stable compound with fivefold bonding between two chromium(I) centers, Science, 310, 844 (2005)
[5] S. Shaik, D. Danovich, W. Wu, P. Su, H. S. Rzepa, P. C. Hiberty: Quadruple bonding in C2 and analogous eight-valence electron species, Nature Chemistry, 4, 195 (2012)
[6] A. J. Arduengo III, R. L. Harlow, M. Kline: A stable crystalline carbene, J. Am. Chem. Soc. 113, 361 (1991)
[7] M. Denk, R. Lennon, R. Hayashi, R. West, A. V. Belyakov, H. P. Verne, A. Haaland, M. Wagner, N. Metzler: Synthesis and structure of a stable silylene, J. Am. Chem. Soc, 116, 2691 (1994)
[8] C. A. Dyker, V. Lavallo, B. Donnadieu, G. Bertrand: Synthesis of an extremely bent acyclic allene (a “carbodicarbene”): a strong donor ligand, Angew. Chem. Int. Ed. 47, 17, 3206 (2008)
[9] G. D. Frey, V. Lavallo, B. Donnadieu, W. W. Schoeller, G. Bertrand: Facile splitting of hydrogen and ammonia by nucleophilic activation at a single carbon center, Science, 316, 439 (2007)
[10] A. Sekiguchi, T. Yatabe, C. Kabuto, H. Sakurai: The "missing" hexasilaprismane: synthesis, X-ray analysis, and photochemical reactions, J. Am. Chem. Soc. 115, 5853 (1993)
[11] A. Sekiguchi, R. Kinjo, M. Ichinohe: A stable compound containing a silicon-silicon triple bond, Science, 305, 1755 (2004)
[12] K. Abersfelder, A. J. P. White, H. S. Rzepa, D. Scheschkewitz: A tricyclic aromatic isomer of hexasilabenzene, Science, 327, 564 (2010)
[13] K. Suzuki, T. Matsuo, D. Hashizume, H. Fueno, K. Tanaka, K. Tamao: A planar rhombic charge-separated tetrasilacyclobutadiene, Science, 331, 1306 (2011)
[14] J. D. Masuda, W. W. Schoeller, B. Donnadieu, G. Bertrand: Carbene activation of P4 and subsequent derivatization, Angew. Chem. Int. Ed. 46, 7052 (2007)
[15] J. D. Masuda, W. W. Schoeller, B. Donnadieu, G. Bertrand: NHC-mediated aggregation of P4: Isolation of a P12 cluster, J. Am. Chem. Soc. 129, 14180 (2007)
[16] O. Back, B. Donnadieu, P. Parameswaran, G. Frenking, G. Bertrand: Isolation of crystalline carbene-stabilized P2-radical cations and P2-dications, Nature Chemistry, 2, 369 (2010)
[17] Y. Xiong, S. Yao, M. Brym, M. Driess: Consecutive insertion of a silylene into the P4 tetrahedron: Facile access to strained SiP4 and Si2P4 cage compounds, Angew. Chem. Int. Ed. 46, 4511 (2007)
