 |
BMe Research Grant |

|
Pál Csonka Doctoral School
Department of Mechanics, Materials and Structures
Supervisor: Prof. Gábor Domokos
The morphology of pebbles
Introducing the research area
 What shape is a
pebble? - the aim of my PhD research is to answer this fundamental question.
What shape is a
pebble? - the aim of my PhD research is to answer this fundamental question.
The great diversity and beauty of pebble shapes have always posed a puzzle
for scientists. The basic idea of the research is that the concept of static
equilibria offers a natural classification system to encode pebble shapes.
In my PhD research I investigate the mathematical background of this new
classification system and apply the system to describe the morphology and
the abrasion process of pebbles.
Brief introduction of the research place
The Department of Mechanics, Materials and
Structures is engaged in a big variety of problems in the field of
mechanics and structural design. Research topics are
not only related to steel, timber, reinforced concrete, composite,
membrane, masonry and adobe structures but there are also ongoing researches in
the areas of earthquake engineering and stability
of structures. Our research area includes a wide range of mechanics and
applied mathematics, in addition to morphology and abrasion processes of
pebbles, and members of our department also investigate the shape dynamics of asteroids,
and the stability problems of colliding bodies and population dynamics.
History and context of the research
 Since Aristotle
[5], many illustrious scientists have been interested in the
geometry of pebbles [6][7]. Pebble shapes attract also considerable attention nowadays
[8][9][10] because investigation of natural shapes formed by abrasion
processes (e.g. landforms, asteroids or pebbles) helps understand abrasion
processes itself. Pebble shapes carry important information on the history of
sediment transport and deposition [11][12], thus an appropriate shape classification helps
differentiate facies.
Since Aristotle
[5], many illustrious scientists have been interested in the
geometry of pebbles [6][7]. Pebble shapes attract also considerable attention nowadays
[8][9][10] because investigation of natural shapes formed by abrasion
processes (e.g. landforms, asteroids or pebbles) helps understand abrasion
processes itself. Pebble shapes carry important information on the history of
sediment transport and deposition [11][12], thus an appropriate shape classification helps
differentiate facies.
Despite the extensive literature on the topic, there is little agreement on
the best classification method for pebble shape analysis [16][17]. Geologists have developed a big variety of standardized
shape indices and shape classification systems for rough estimation of pebble
morphology [12][13][14][15]. These classical methods rely on length
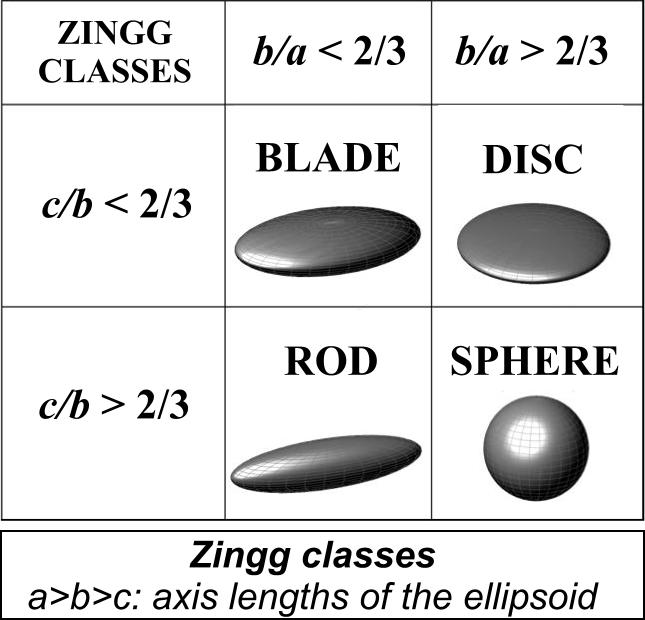
measurements, the simplest and most widespread classification system set up by Zingg [15] who proposed approximating pebbles with a three-axial
ellipsoid and classified shapes based on the axis ratios. While these classical
systems have undoubtedly proved to be useful tools, their application inevitably
requires tedious and ambiguous measurements, and the classification involves the
introduction of arbitrarily chosen constants.
The research goal, open questions
The aim of my research is to propose a new and completely different classification system for pebble morphology. As the new system does not rely on length measurements it does not suffer from ambiguities in classical methods. Our method is readily applicable in field work as well. The new classification system encodes shapes based on the number and type of static equilibria and the relationships between equilibrium points.
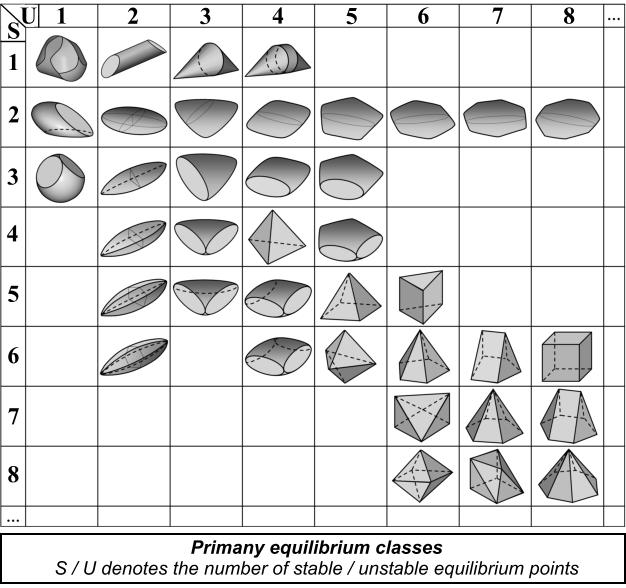
The basis of the code is the number of stable and unstable equilibrium points. Based on these two natural numbers every homogeneous, convex body can be classified unambiguously [18], and the result is called the primary equilibrium class of the body. For example, the cube belongs to class {6,8} because there is a stable point on each of the 6 faces and each of the 8 vertices is an unstable point. The Gömböc [19], invented by Gábor Domokos and Péter Várkonyi belongs to class {1,1} (mono-monostatic body).
Morphology can be more accurately described if we take qualify the equilibrium points if they are neighbours or not. These adjacency relationships define a graph on the pebble's surface, which is called the secondary equilibrium class of the body.
The above described classification system can be further refined with the concept of imaginary equilibrium points. Through the "magnifying glass" we can observe numerous microscopic equilibrium points on the pebble's surface: these are the real equilibria of the pebble. However, outside observer cannot discriminate microscopic real equilibria by eye because they occur in highly localized groups (flocks) [3][4] on the surface, thus human experimenter perceives only these flocks as imaginary equilibria.
My PhD research includes the mathematical study of the new classification system based on primary, secondary, imaginary and real equilibria, as well as the practical application of the new system to examine pebble morphology.
The other main goal of my research is to understand and model abrasion
processes of pebbles, especially considering the above described new
classification system. Our system uses only natural numbers, thus every shape
can be described by a code and change of the code can be followed up with the
appropriate mathematical and technical tools if we measure the body's code
systematically during the abrasion process. The aim of the research is to
understand the changes in the morphology through the changes of code, and to
assign different code sequences to different abrasion processes.
Methodology
 Imaginary
equilibrium points of a pebble can be counted in simple and fast hand
experiments. Typical 3D bodies may have three types of equilibrium points:
stable equilibria, unstable equilibria and saddle points; their number will be
denoted by S, U and H, respectively. The Poincare-Hopf
Theorem [20] establishes the relationship S+U-H=2 for bodies
with spherical topology, hence we only have to count stable and unstable
equilibrium points, the number of saddle points can be computed. Based on
hand experiment, {S,U} is the primary class corresponding to imaginary
equilibria of the pebble.
Imaginary
equilibrium points of a pebble can be counted in simple and fast hand
experiments. Typical 3D bodies may have three types of equilibrium points:
stable equilibria, unstable equilibria and saddle points; their number will be
denoted by S, U and H, respectively. The Poincare-Hopf
Theorem [20] establishes the relationship S+U-H=2 for bodies
with spherical topology, hence we only have to count stable and unstable
equilibrium points, the number of saddle points can be computed. Based on
hand experiment, {S,U} is the primary class corresponding to imaginary
equilibria of the pebble.
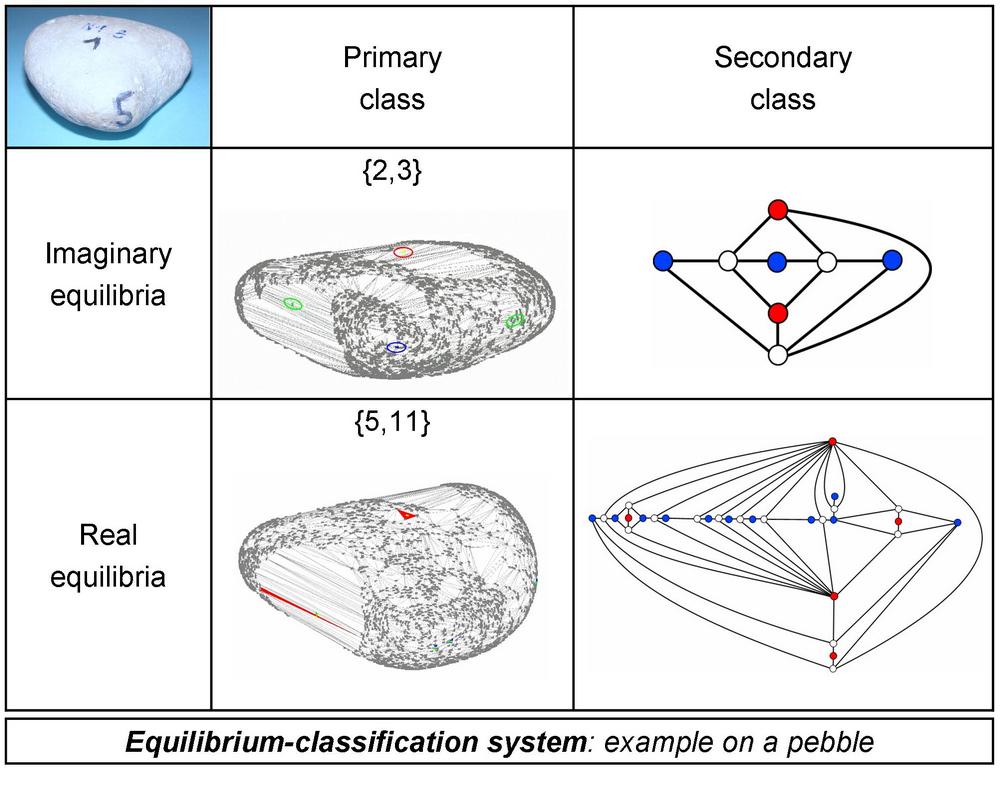
Identifying real equilibria on a pebble is a more complex task, however, the information contained is also more detailed. Microscopic real equilibria can be detected by modern 3D scanning technology, the high-accuracy (0.1 mm) scanning was performed at the Department of Manufacturing Sciences and Technology, using a 3D laser scanner mounted on a CNC machinery. The result of the scanning process is a many-faceted, triangulated polyhedral surface, on which equilibrium points can be identified by an appropriate computer algorithm.
Secondary class is determined by
the topology of the Morse–Smale-complex [21] which is built up by the heteroclinic
orbits between equilibrium points. The topology of this
Morse–Smale complex can be illustrated by a planar graph: equilibrium points are
the vertices of the graph and there is an edge between two equilibrium points if
they are neighbours on the pebble's surface. The graph corresponding to real
equilibria can be simplified with a known algorithm [21] until microscopic real equilibrium points disappear and
only the macroscopic, imaginary equilibria remain that can be observed by hand
experiments. Geometrically, simplification of the Morse–Smale complex
corresponds to the "smoothing" of the polyhedral surface.
Results

Determining the number of imaginary equilibrium points can be done in seconds by very simple and
fast hand experiments. This promises to be of great
advantage in geological field-work. Despite the simplicity of this code, these
two natural numbers describe the geometry of the pebble adequately since there
is a strong relationship between the Zingg-classes and primary (imaginary)
equilibrium classes. Based on data of 1000 measured pebbles we found that the
simplified version of equilibrium classification contains all the information
contained in the Zingg system, with up to 10-20% inaccuracy [1][2]. However, the new system is more sophisticated: it may help
to identify shape attributes unexplored so far as it is able to store
information on special geometries, e.g. on crystal shapes [2]. Primary class is also closely connected to roundness: as an
example we mention that the classical Zingg system cannot make a difference between
tetrahedral and cubic shapes, while equilibrium classes {4,4} and {6,8} give
clear descriptions of these shapes.
Using the above described 3D scanning
technology, we showed that microscopic real equilibrium points on pebbles are
accumulated in highly localized groups (flocks), the latter can be
perceived as imaginary equilibrium points in hand experiments. Except for
spherical pebbles, the scales of real and imaginary equilibria (micro- and
macro-equilibria) are well separated [3], thus imaginary equilibria (flocks) can be reliably counted
in a hand experiment, i.e. our new classification system is practically
applicable.
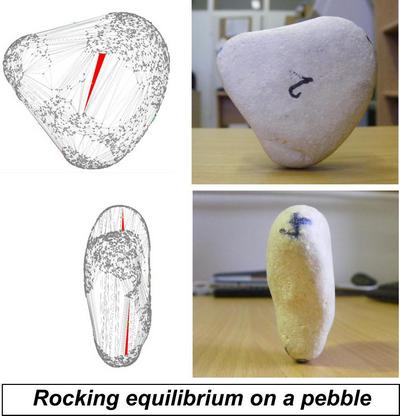
The concept of real and imaginary equilibria provides a framework to explain
an interesting phenomenon: the amazing and counter-intuitive equilibrium
position of rocking stones. These
large stones are so sensitively balanced that despite their large mass, even a
small force applied causes them to rock. Because of their strange attitude, rocking
stones were connected to plenty of beliefs in the past, e.g. they were associated
with witchcraft. Rock-balancing
artists produce similar but smaller scale artworks. We introduced the
concept of rocking equilibrium to explain this phenomenon [3]: rocking equilibrium is a stable real equilibrium belonging
to an unstable imaginary equilibrium. The concept of rocking equilibrium clearly
explains why we feel that equilibrium position of rocking stones is
counter-intuitive: outside observer does not perceives the microscopic stable
equilibrium point, only the macroscopic unstable (imaginary) equilibrium.
Expected impact and further research
In the course of further research we plan to perform meaningful field
measurements in which we collect pebble samples from locations of geological interest. A thoughtful selection of geological locations allows us to examine
different depositional environments to follow up and distinguish different
abrasion processes. Besides this, we plan to perform laboratory experiments and
we work on numerical and analytical models of abrasion processes. Our final goal
is to understand and model different abrasion processes of different
depositional environments, using the new classification system to encode shapes.
Publications, references, links
Publications:
[1] G. Domokos, A. Sipos, T. Szabó, P. Várkonyi (2010). Pebbles, Shapes, and Equilibria. Mathematical Geosciences, Vol 42, 29-47.
[2] T. Szabó, G. Domokos (2010). A new classification system for pebble and crystal shapes based on static equilibrium points. Central European Geology, Vol 53/1, 1–19
[3] G. Domokos, A. Sipos, T. Szabó. The mechanics of rocking stones: equilibria on separated scales. Submitted to Mathematical Geosciences. Manuscript
[4] G. Domokos, Zs. Lángi, T. Szabó. On the equilibria of finely discretized curves and surfaces. Submitted to Monatshefte für Mathematik. Manuscript
Links:
BME Department of Mechanics, Materials and Structures
Rocking stones:
Youtube: Bill Dan
rock-balancing artist
References:
[5] Aristotle, in Minor Works, Mechanical Problems, Question 15, translated by W. S. Hett (Harvard University, Cambridge, MA, 2000)
[6] Lord Rayleigh (1942). Pebbles, natural and artificial. Proc. Roy. Soc. London A, Vol 182, 107-118
[7] F.J. Bloore (1977).: The shape of pebbles. Mathematical Geology, Vol 9, 113-122
[8] W. Ashcroft (1990). Beach pebbles explained. Nature, Vol 346,
227
[9] M. Lorang, P.D. Komar (1990). Pebble Shape. Nature, Vol 347,
433-434
[10] T. Yazawa (1990). More pebbles. Nature, Vol 348, 398
[11] D.J. Graham, N.G. Midgley (2000).: Graphical representation of particle shape using triangular diagrams: an Excel spreadsheet method. Earth Surface Processes and Landforms, Vol 25, 1473-1477
[12] E. Sneed, R.L. Folk (1958).: Pebbles in the lower Colorado River, Texas, a study in particle morphogenesis. J Geology, Vol 66, 114-150
[13] W.C. Krumbein (1941). Measurement and geologic significance of shape and
roundness of sedimentary particles. J Sed Petr, Vol 11, 64-72
[14] C.K.
Wentworth (1922). The shapes of beach pebbles. US Geological Survey Professional
Paper, Vol 131-C, 75-83.
[15] T. Zingg (1935). Beitrag zur Schotteranalyse. Schweizer Miner. Petrog. Mitt., Vol 15, 39-140
[16] W. Illenberger (1991). Pebble shape (and size!). J. of Sedimentary
Research, Vol 61, 756
[17] S.J. Bott, K. Pye (2008). Particle shape: a
review and new methods of characterization and classification. Sedimentology Vol
55, 31-63
[18] P. Várkonyi, G. Domokos (2006). Static equilibria of rigid bodies: dice, pebbles and the Poincaré-Hopf Theorem, J Nonlinear Sci, Vol 16, 255-281
[19] P. Várkonyi, G. Domokos (2006). Mono-monostatic bodies: the answer to Arnold’s question, The Mathematical Intelligencer Vol 28, 34-38
[20] V.I. Arnold (1998). Ordinary differential equations. 10th printing, MIT Press, Cambridge.
[21] H. Edelsbrunner, J. Harer, A. Zomorodian (2003). Hierarchical Morse-Smale complexes for piecewise linear 2-manifolds. Discrete Comput Geom Vol 30, 87-107
