 |
BMe Research Grant |
|
Doctoral School in Mathematics and Computer Science
Department of Stochastics/Institute of Mathematics
Supervisor: Károly Simon
Mathematics of the Internet – Modeling networks with random graphs
Introducing the research area
My research interest is focused on Internet-related mathematical questions, most importantly, on the theory of different network models. Our aim is to describe and present network models that share properties similar to many of the most important real networks, like ones with hierarchical structure combined with scale-free degree distribution, or those consisting of small, well-wired communities connected by weak edges. These and similar models gain high interest in both the mathematical and applied sciences.
Brief introduction of the research place
The research takes place at the the Department of Stochastics of BME, which is considered the strongest Central European research place in the field of probability and stochastics. Our professors, Domokos Szász (vice president of the Hungarian Academy of Sciences, dynamical systems), Bálint Tóth, (head of department, long-memory random walks) and Károly Simon (random and deterministic fractals) publish in the best reputed journals and are plenary speakers of conferences of the field. The younger generation is represented by internationally recognized researchers like Márton Balázs (interacting particle systems), Péter Tóth (dynamical systems) and Balázs Székely (applied probability). An outstanding probability seminar held in Hungary, the Stochastic Seminar attracts the most prestigious researchers to give lectures. A most important strength of our department is the high rate of excellent young researchers brought up here during the last decade. Most of the graduate students are offered postdoctoral positions at leading universities in the USA or in Europe after PhD and become successful researchers.
History and context of the research
Five institutes (including the Math Institute at BME) have won a consortial project (filed with OTKA NKTH no. 77778) for the research of future Internet. The leader of the project is professor Károly Simon. My research aims at providing new results in the field of Internet related mathematical questions. Since this area is new at our department, it was (and still is) very important for us to establish and maintain connections with leading Hungarian and foreign research groups in the field. I have spent three months at the Theory Group of Microsoft Research, working with Yuval Peres – two joint papers are in process. We also collaborated with Anna Karlin, (University of Washington), and this work yielded topics for MSc and BSc thesis of our students. We also started a joint work on the modeling of communities in social networks with professor Béla Bollobás, one of the most famous researcher of the mathematics of random graphs. As a starting point of this joint work served the social network models of János Kertész (BME, Institute of Physics, complex networks). We also contacted Tamás Vicsek (ELTE). The paper [A] where we generalized the deterministic scale-free network model he and his coauthors introduced in [1] has been accepted by Chaos, Solitons and Fractals and will be published soon. I present the content of this paper below.
The research goal, open questions
In the last two decades, a considerable amount of attention have been paid to the study
of complex networks like the World Wide Web, social networks, or
biological networks.
This resulted in the construction of
numerous network models, which try to model different properties of real
networks.
An important feature in most real networks is the scale-free property,
i.e., for a randomly chosen vertex in the graph, the number of edges starting
from the node has distribution with
power law decay. This means that high proportion of the vertices have very small
degree but there are also some vertices which have enormously many edges. Most
models having this property use a version of preferential
attachment and are of probabilistic nature. A completely different approach
was initiated by Barabási, Ravasz and Vicsek [1]. The
deterministic network models they introduced were generated by a
method commonly used in constructing fractals. Their models
exhibit hierarchical structure and the degree sequence obeys power law decay with exponent 1+log3/log2. To model the clustering
behavior of real networks as well, Ravasz and Barabási [2]
enhanced the original model so that their deterministic network model preserved the same power law decay and features a
clustering behavior similar to many real networks. Namely, the
average local clustering coefficient is independent of the size of the
network and the local clustering coefficient decays inversely
proportional to the degree of the node.
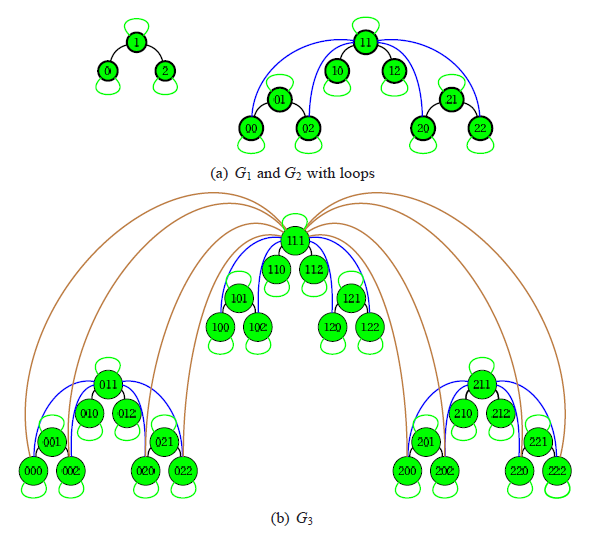
In our research we aimed to generalize
the model in the sense that we generate a graph sequence with hierarchical
structure obeying power law degree distribution with exponent γ,
which can be arbitrary in a given range. (An interesting case is the modeling of
networks with γ between 1 and 2, where the expected value of degree
distribution tends to infinity.) Another goal was to
randomize the model and produce random graphs with closely-hierarchical
structure with a given power law exponent.
We also aimed to give
mathematically rigorous proofs of statements about graph-theoretical properties
of the network (average shortest path, diameter, behavior of local clustering
coefficient as the function of the degree of the given node).
Methodology
After appropriate coding the vertices of the graph, we mapped
the adjacency matrix of the
graphs in the unit square (see the picture below) and then
we proved convergence of this embedding. (In the picture
below, each colored square corresponds to an edge of the same color in the
picture above). We showed that this sequence of sets converges to the
attractor of a graph-directed self similar set. The geometrical properties of
the set are characterized by the corresponding iterated function
system.
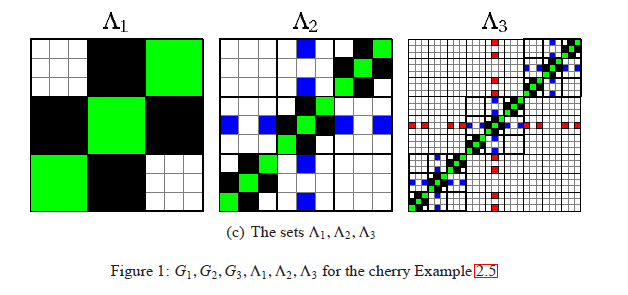So, we translated the graph sequence into the language of
fractals: the hierarchical structure corresponds to the fact that the next set
consist of little copies of the previous set, positioned in the diagonal of the
unit square. The edges connecting different copies are in the off-diagonal domain and
are converging to a self-similar fractal.
With this new
description we managed to generate hierarchical graph sequences starting from
arbitrary bipartite graph, and to derive their properties from the coding of
vertices and from the fractal.
Results
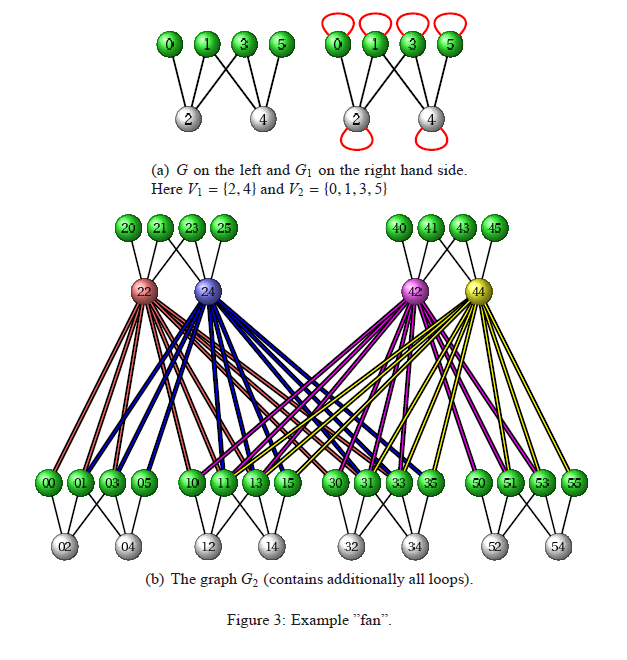
Starting from any
bipartite graph, we can define the corresponding hierarchical graph sequence
(an example can be seen in the figure on the right). The
power law exponent of the degree distribution can be determined from the initial
graph, or from the Hausdorff dimension
of the fractal coming from the embedded adjacency matrix in the unit square:
It is most interesting if the initial graph
has more edges than vertices. We proved that in this case the exponent γ is a quotient: the numerator is the Hausdorff dimension of the
intersection of the fractal with a line randomly thrown through it, and the
denominator is the Hausdorff dimension of the intersection of the fractal with a
vertical line. (see the picture below).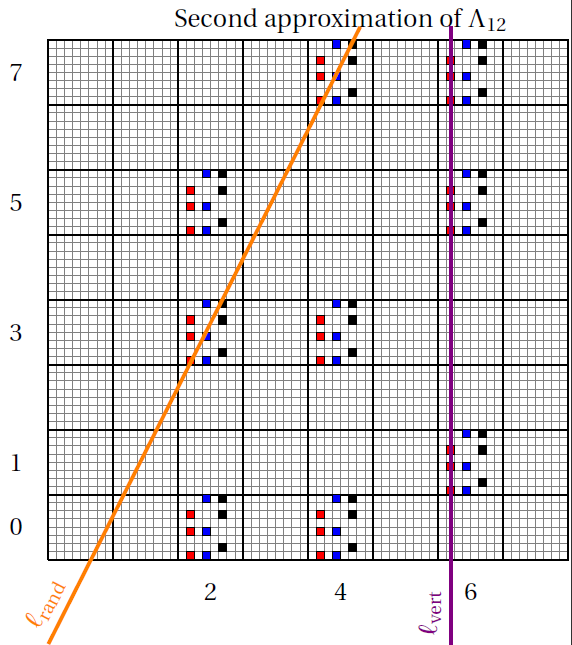
Using the appropriate coding of vertices we proved that the diameter of
the graph is proportional to the logarithm of the number of vertices.
Additionally, we showed that the expected length of the shortest path between two
random vertices is of the same order. Considering the slightly modified version
of the model we proved that the local clustering coefficient of any vertex is
proportional to 1/degree of the node, which is a rigorous proof of argumentations based on simulation
results.
Finally, we randomized the
model, which randomization can be described by the following probabilistic
interpretation: Imagine a deterministic graph sequence, where each node is replaced by an urn. Now take a number of balls, so that every urn receive on average as many balls as the number of vertices in the initial smallest graph. Drop
these balls independently and uniformly at random into the urns. In our random
graph each vertex corresponds to a ball, and two vertices are connected by an
edge if the corresponding balls landed in urns connected in the deterministic
graph. We proved that the random graph sequence we get by this method shares the
same power law exponent γ as the deterministic one.
Expected impact and further research
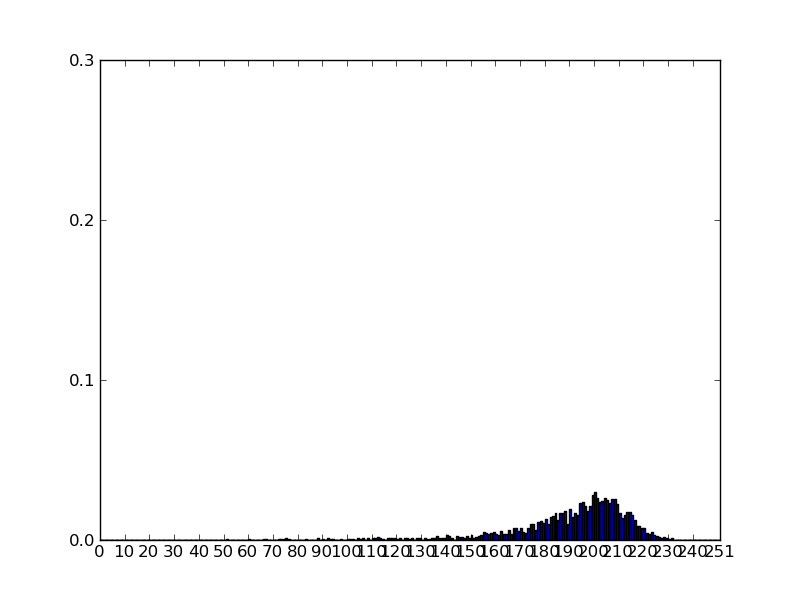
The model presented here has been accepted and will be published in the coming days in the Chaos, Solitons and Fractals journal. Our further research in this topic concentrates on a model initiated by János Kertész and his research group. This model is a dynamically improving network, which shares features similar to social networks. Namely, the links in the graph are strong within communities, and edges connecting communities are mainly weak. An important question is to determine the distribution of the largest community size, and the time it takes for this distribution to stabilize. The stabilized distribution of the largest component is shown in the picture to the right.
Publication, references, links
Publications
[A] J. Komjáthy, K. Simon. Generating hierarchical scale-free graphs from fractals. Chaos, Solitons & Fractals (2011), doi:10.1016/j.chaos.2011.05.012
[B] J. Komjáthy, J. Miller, Y. Peres. A tight bound of the uniform mixing
time of lamplighter walks. In preparation.
Links
Department of Stochastics, BME
Microsoft Research,
Theory Group
Complex Networks
Research Group, Department of Theoretical Physics, BME
References
[1] A.-L. Barabási, E. Ravasz, T. Vicsek, Deterministic Scale-Free Networks. Physica A: Statistical Mechanics and its Applications 299, Issues 3-4 559–564 (2001) 559–564.
[2] E. Ravasz, A.-L. Barabási. Hierarchical organization in complex networks. Phys.Rev. E 67 (2003) 47 026112.
[3] B. Bollobás. Random graphs. Cambridge University Press,
2001.