 |
BMe Kutatói pályázat |

|
BME Vásárhelyi Pál Építőmérnöki és Földtudományi Doktori Iskola
BME Hidak és Szerkezetek Tanszéke
Témavezető: Dr. Bódi István
Vasalt és vasalás nélküli téglafalazatok kísérleti és numerikus vizsgálata
A kutatási téma bemutatása
A tégla az egyik legrégebbi idők óta ismert építőanyag, amit már az ókori Mezopotámiában is használtak. Annak ellenére, hogy ilyen hosszú ideje alkalmazzák, a téglafalazatok viselkedése az egyik legkevésbé ismert a mérnökök számára az építőanyagok közül.
A falazott szerkezetek alkalmazása hazánkban nem olyan sokrétű, mint a tengerentúlon vagy Európa északnyugati részén. Itthon a magasabb falazott épületeket vasbeton vázzal együtt építik, a téglafalazatnak csak kitöltő szerepe van. Amerikában és Angliában gyakran építenek 4-10 emeletes teherbíró falszerkezeteket vasbeton keretváz nélkül. Az elmúlt évek tapasztalatai szerint ez legtöbbször vasalt téglafalazatok építésével valósítható meg, mely olcsóbb, gyorsabb és környezetbarátabb eljárás, mint az itthon alkalmazott vasbeton falazati rendszerek.
A falazatok nyomással szembeni ellenállása elegendő ahhoz, hogy a közepes szintszámú épületekben keletkező függőleges
erőket az alapig közvetítsék tönkremenetel nélkül. A vízszintes irányú terhekkel
(pl. szél, földrengés) szembeni ellenállásuk és alakváltozási képességük azonban
csekély. Magyarországon az elmúlt évtizedig a földrengés miatti követelményeket
nem kellett tervezéskor ellenőrizni. A földrengésre vonatkozó egységes európai
szabvány, az Eurocode 6 bevezetésével a tervezési követelmények kizárólag
téglafalazat alkalmazásával nehezen elégíthetőek ki a 2-3 emeletesnél
magasabb épületek esetében. Ha függőlegesen vagy vízszintesen betonacélt
helyezünk el a hézagokban, a fal alakváltozási képessége megnő, teherbírása és
rendkívüli terhekkel (pl. ütközés, földrengés, rezgések) szembeni ellenállása is
kedvezően változik. [1, 2, 3, 4]
A kutatóhely rövid bemutatása
Az Építőmérnöki
Kar Hidak és Szerkezetek Tanszéke főként a föld
feletti létesítmények erőtani tervezésével, méretezésével és vizsgálatával
foglalkozik. Tanszékünk rendelkezik a kar legnagyobb, szerkezetek vizsgálatára is alkalmas
laboratóriumával, mely a kutatáshoz és a tervezéshez
szükséges számos kísérletnek ad otthont. Tantárgyaink többsége a híd- és
szerkezettervezési szakirányt választó mérnökök szakmai tudását alapozza
meg.
A kutatás történetének, tágabb kontextusának bemutatása
A vasalt falazatokkal foglalkozó nemzetközi szakirodalomban olyan rendszerek találhatók, ahol a függőleges vasalás az erre a célra kifejlesztett falazóelem belsejében halad, vagy a téglákat olyan speciális kötésben helyezik el, amelynek közepében vasbeton oszlop alakítható ki. Mindkét esetben betonnal töltik ki a betonacél körüli üregeket. Ezen falak viselkedését és fent említett pozitív tulajdonságait számos kutató vizsgálta és kísérletileg igazolta. Minden terhelési esetre, alkotóelem-típusra és elrendezésre kísérletet végezni nagyon költséges. Numerikus modellek alkalmazásával olyan virtuális kísérletek is elvégezhetők, amelyekre a valóságban nincs technikai vagy anyagi lehetőség. A téglaszerkezetek esetében ez különösen fontos, hiszen felesleges minden kötéstípust, elrendezést és terhelési típust kísérlettel vizsgálni.
A modellezés alapvető feltétele, hogy ismerjük az alkotóelemek mechanikai jellemzőit. A falazóelemek, habarcsok és gyártóik sokfélesége miatt nemcsak az egyes anyagok mechanikai jellemzői különböznek, hanem az egyforma anyagokra rendelkezésre álló szakirodalmi adatok is nagyon eltérnek. A hazai gyártók nem rendelkeznek a falazóelemek minden jellemzőjével, és csak az összeépített falazatok tulajdonságainak vizsgálatára léteznek szabványos vizsgálati előírások.
Az említett okok miatt foglalkozik anyagvizsgálatokkal és modellezési problémákkal a teherhordó falazatok témakörében kutatók jelentős része. A falazatok és más szerkezetek vizsgálatára a diszkrét és végeselemes eljárások a szakirodalomban leginkább elterjedt numerikus szimulációs módszerek. A vizsgálat módszeréül választott diszkrét elemes modellezés kevésbé ismert eljárás. Olyan 3 dimenziós falszerkezeti diszkrét elemes modellezéssel kapcsolatban, amelyhez kísérleti adatok is rendelkezésre állnak, még nem jelent meg publikáció.
A kutatás célja, a megválaszolandó kérdések
A doktori értekezés elkészítése egy olyan többéves kutatási program első szakasza, mely a legnagyobb magyar téglagyártó és egy nemzetközi mérnöki szoftverfejlesztő céggel együttműködésben folyik. A végső cél az, hogy létrehozzunk egy olyan építési módszert, amely a magyarországi téglatípusokhoz, építési rendszerekhez igazodva biztosít nagyobb alakváltozási képességet a téglafalazatoknak, ezáltal lehetőség nyílik alkalmazásukra a nagyobb szintszámú épületek esetében is. A tervezés egyszerűsítése céljából meg kell határozni, hogy a falazaton belül milyen kötéskialakítással, hova helyezzünk el betonacélt a lehető leggazdaságosabb megvalósítás érdekében. Ennek tükrében javaslat tehető a falazóelemek gyártóinak a megfelelő elemválaszték kialakítására.
A tervezett kutatás elsődleges célja a magyar habarcs és tégla szakirodalomból hiányzó anyagjellemző paramétereinek meghatározása. Ezek alapján kidolgozható egy vasalatlan falazatokat modellező eljárás, amely modell viselkedése kísérletekkel igazolható. A tervezett célok között szerepelt egy új kötéstípus kidolgozása vasalt falazatra, hagyományos téglafalazathoz viszonyított előnyeinek és hátrányainak feltárása és vízszintes terhekkel szembeni kedvező viselkedésének igazolása. Kísérletek alapján a vasalt falazatokra is létrehozható modell, amellyel igazolható, hogy kizárólag vasalt téglafalazat segítségével 2-3-nál nagyobb szintszámú épület is megépíthető a tervezési előírások betartása mellett.
Módszerek
Összegyűjtöttem, csoportosítottam és tipizáltam a vasalás nélküli falazatok tönkremeneteli lehetőségeit különböző típusú és irányú terhelési esetekre. A vasalással ellátott falazatok tönkremeneteli módjainak (a vasalás hogyan befolyásolja a repedésképet, a teherbírási- és az alakváltozási képességet) megállapítására kísérleteket végeztem. Megállapítottam, hogy a tönkremenetel vasalt téglafalazatok esetében is – a vasalás nélküli falazathoz hasonlóan – leggyakrabban a habarcs és a téglafelület találkozásánál történik.
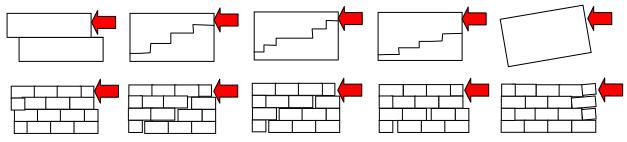
1. ábra: A tönkremeneteli típusok vízszintes erővel történő terhelési esetre
A falazatok modellezésére
három elterjedt módszer található a szakirodalomban. Az első, amikor a habarcsot
és falazóelemet külön-külön modellezik (2. a ábra), a második, amikor csak a
falazóelemet (b). A harmadik módszer az, amikor az alkotóelemeket nem ábrázolják
külön, csak az egész falazatot, egy összefüggő kontinuumként (c).
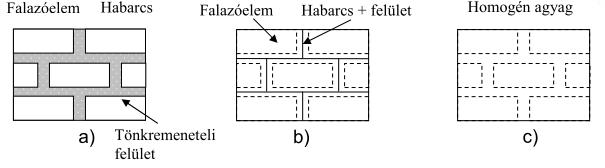
2. ábra: A téglafalazatok modellezési lehetőségei: a) mikromodell, b) egyszerűsített mikromodell, c) makromodell
Mivel a tönkremenetel a vasalt és vasalás nélküli falazat esetében is legtöbbször a két elem kapcsolatánál következik be és nem a habarcsban, ezért ha a modellezési feltételek engedik, lehetőség van mindkét esetre egyszerűsített mikromodell alkalmazására.
Egy 2D diszkrét elemes modell segítségével
meggyőződtem arról, hogy a modellezési paraméterek megfelelő megválasztásával elérhető
a vasalatlan falazat esetén szimulálható valamennyi vasalt és vasalatlan
falazatra jellemző tönkremeneteli mód. [15]
A tervezett 3D falazati modell megfelelőségének
igazolására három feltételt tűztünk ki:
1. A szakirodalomban jól meghatározott, és a kapcsolati viselkedést megfelelően bemutató kísérletekkel megegyező kapcsolati viselkedés,
2. Az általam kimért tégla anyagjellemzők alkalmazásával kapható és az elvégzett kísérlettel megegyező repedéskép,
3. A modellezett és a kísérletben felépített valódi szerkezet ugyanazon pontján alkalmazott erő hatására a szerkezet mindkét esetben ugyanakkora alakváltozást szenvedjen.
A diszkrét elemes modellezés kulcskérdése általában a
megfelelő mechanikai anyagjellemzők és egyéb, kísérlettel nem meghatározható
paraméterek megadása. A szakirodalomban fellelhető, ezekre vonatkozó
ellentmondásos és hiányos adatok miatt szükséges volt saját mérések elvégzésére.
A Hidak és Szerkezetek Tanszék szerkezetvizsgáló laboratóriumában és az Építőanyagok és Mérnökgeológia Tanszék anyagvizsgáló laboratóriumában roncsolásos és roncsolásmentes vizsgálatokat végeztem a tégla méret- és irányfüggő tulajdonságainak meghatározására. Ezen kívül vasalatlan, vízszintes, függőleges, és mindkét irányú vasalással ellátott falazatok vízszintes, statikus terhekkel szembeni viselkedéseinek meghatározására laborkísérleteket végeztem. Az alábbi hivatkozásra kattintva megtekinthető egy falazat tönkremenetelének videója.




3. ábra: Az elvégzett kísérletek egy része
Eddigi eredmények
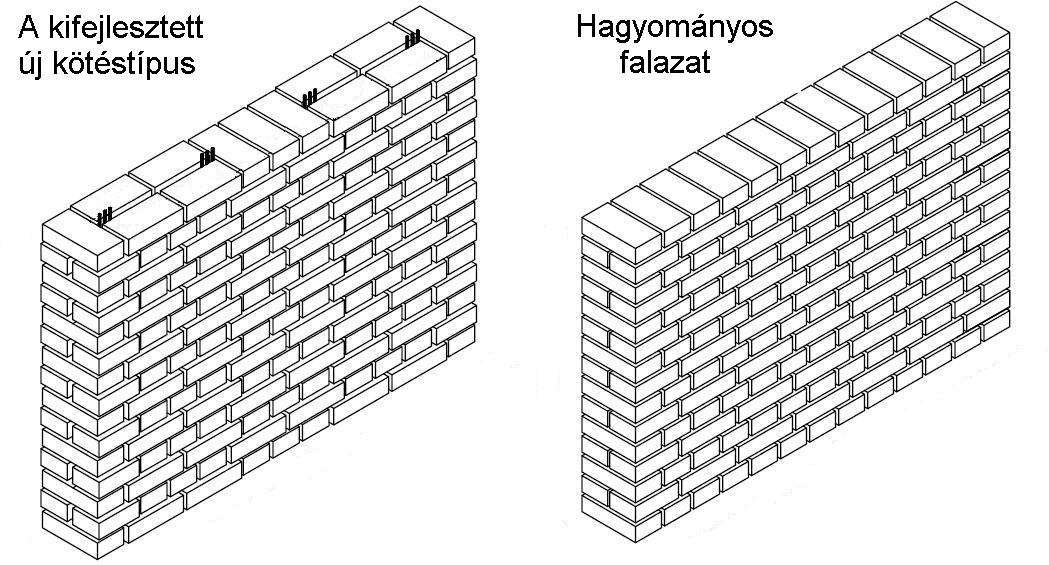
1. Kidolgoztam egy egyedi téglakötési típust, amely lehetővé teszi függőleges
és vízszintes acélbetétek elhelyezését a falazatban, a téglakötés szabályainak
megsértése nélkül és az eddigi rendszereknél sokkal kisebb méretű üreget
biztosít a vasalás elhelyezésére. Ez a rendszer egyedülálló a vasalt falazatokat
tekintve, mivel ugyanaz a habarcs használható a vízszintes fugák és a függőleges
üregek kitöltésére. [5, 7]
2. Az új rendszer viselkedésének igazolására
számos falazatból álló kísérletsorozatot végeztem, két típusú habarcs
alkalmazásával. Bebizonyítottam, hogy a hagyományos falazattal összehasonlítva
az első repedések több mint 2x nagyobb alakváltozás esetén jelennek meg, 20%-kal
magasabb teherszinten. A végső tönkremenetelig 10x nagyobb alakváltozásra képes,
mint a hagyományos falazat. Ez a típusú kialakítás más falazati rendszereknél
ott előnyösebb, ahol bármelyik irányban érheti teher a falat: foghíjtelek
beépítésekor, robbanás-, vagy földrengésveszélyes területeken, tűzfalak,
támfalak esetében. [8, 9]
3. Kísérletek segítségével elemeztem a jellemző
tönkremeneteli mechanizmusokat, és meghatároztam az azokat befolyásoló
paramétereket. Ezek alapján a mérnökök
tervezési munkáit könnyítő méretezési eljárást javasoltam az ilyen kötésben
készült vasalt falazatok vízszintes terhekkel szembeni vizsgálatára. [10]
4. A Wienerberger Zrt.-vel szoros együttműködésben meghatároztam a
tégla azon mechanikai jellemzőit, amelyek a gyártó számára nem ismeretek, de a
tervezéshez elengedhetetlenül szükségesek. Több mint száz próbatesten végeztem
kísérleteket, és tisztáztam a szakirodalmi ellentmondások okát.
Megállapítottam, hogy a tégla minden terhelési irányban eltérő viselkedést
mutat. Meghatároztam, hogy a kísérlettel nyerhető anyagjellemzők milyen
mértékben függnek az alábbi paraméterektől: a felület érdessége, a próbatest
magassága, szélessége, hosszúsága és alakja, a mintavételezés típusa
(fúrt, vágott), a terhelés iránya. Kimértem a Magyarországon alkalmazott habarcs
tervezési szempontból lényeges mechanikai jellemzőit több mint félszáz habarcs
próbatesten. [13]



5. A kísérletekben nyert mechanikai jellemzők
felhasználásával a 3DEC 3 dimenziós diszkrét elemes programmal modelleztem a
tégla és a habarcs közötti kapcsolatot. Ezek alapján egy olyan modellt
készítettem hagyományos, kisméretű téglából készült téglafalazatra, amellyel
elérhető a kísérletivel azonos töréskép (6. a ábra), megfelelő a teherbírás
meghatározására, és a kísérletivel megegyező alakváltozást szolgáltat. A
felépített modell alkalmas az elvégzett kísérletek szimulálására, és megfelelő
paraméterválasztással szimulálni
tudja a valós falazat viselkedését a kísérletekben alkalmazott terheléseknél. A kialakított modellben a falazatban
található elemek mérete, elrendezése, tulajdonságai és terhelési iránya is
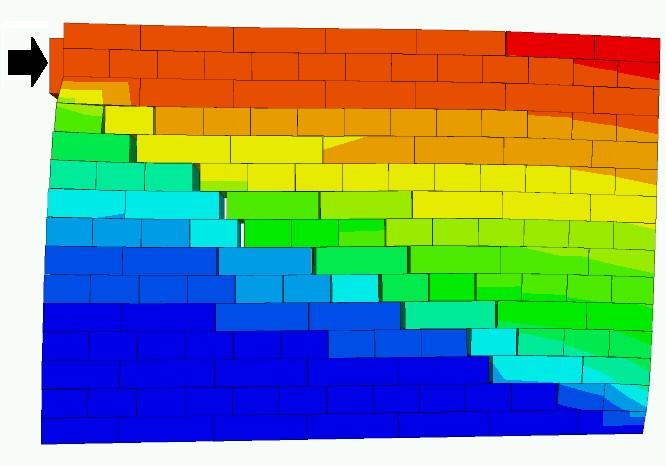
tetszőlegesen változtatható. A 6. b ábrán a falazat egy tönkremenetele
látható abban az esetben, ha egy nagy sebességű tárgy csapódik a középső
téglának [14] (a hivatkozásra
kattintva megtekinthető a szimuláció videója).
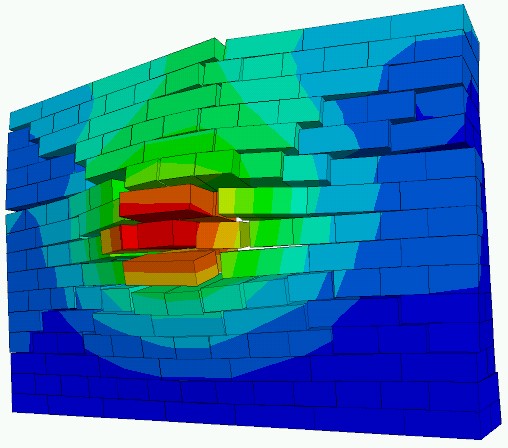
6. Kimutattam, hogy megfelelő paraméterválasztással a vasalatlan falazatok diszkrét elemes modellje vasalt falazatok tönkremeneteli módjainak szimulálására is alkalmas. További kutatási cél más téglatípusok és vasalt falazati rendszerek vizsgálata.
Várható impakt, további kutatás
A kifejlesztett építési rendszer további vizsgálatával olyan téglafalazat-építési eljárás valósítható meg, amely kielégíti a földrengési tervezésre vonatkozó követelményeket magasabb épületek esetében is. Számos téglafalazat vízszintes terhekkel szembeni vizsgálata és a numerikus modellel való összehasonlításuk alapján javaslatot tettem a falazatok modellparamétereinek célszerű megválasztására. Az elvégzett munka nagy segítséget nyújthat a téglafalazatok numerikus modellezésével foglalkozó vizsgálatokban.
A több mint száz téglaelem és majd félszáz habarcs próbatest felhasználásával meghatározott anyagjellemzőkre vonatkozó kísérletek fontos alapját képezhetik további kutatásoknak, értekezéseknek. A továbbiakban egy olyan, nagyobb léptékű modell kialakítását tervezzük, mellyel épületek modellezésére is lehetőség van, és amellyel bizonyítható, hogy ez a falszerkezeti rendszer előnyösen alkalmazható merevítőfalként a 3-5 szintes épületek esetében.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
[1] Fódi A.,
Megvalósult, hagyományos épületek szeizmikus vizsgálatának tanulságai, Doktori Kutatások a BME Építőmérnöki Karán (szerk.
Barna Zsolt), Budapest, 2007. november 14., 93–102.
[2] Fódi A., Bódi I.,
Reinforced masonry structures – European history – Hungarian present practice, Proceedings of the 6th International Conference Analytical Models and New
Concepts in Concrete and Masonry Structures, Łodź, Lengyelország,
2008-06-09-2008-06-11, 1–8. (cikk
megnyitása)
[3] Fódi A., Bódi I., Status
of reinforced masonry in Hungary, Proceedings of the 4th Central European
Congress on Concrete Engineering: Concrete Engineering in Urban Development
(szerk.: Jure Radic, Jelena Bleiziffer), Opatija, Horvátország,
2008-10-02-2008-10-03., 517–522.
[4] Fódi Anita, Megépült középmagas vasbetonvázas épület szeizmikus vizsgálatának tanulságai, Magyar Építőipar, 59:3 kötet, 2009/3., 96–100.
[5] Fódi A., Bódi I.,
Tömör téglából épített vasalt és vasalás nélküli téglafalazat kísérleti és
numerikus vizsgálata saját síkjában történő nyírásra, ÉPKO2009, XIII.
Nemzetközi Építéstudományi Konferencia, Erdélyi Magyar Műszaki Tudományos
Társaság (szerk.: Köllő Gábor), Csíksomlyó, 2009. június 11-14.,
144–151.
[6] Fódi A., Falazott szerkezetek alkalmazása, Tanulmány a Wienerberger Zrt. részére, 2009
[7] Fódi A., Bódi I., Shear
capacity and crack pattern of reinforced and plain masonry walls, 8th fib PhD
Symposium in Kgs. Lyngby, Denmark, Lyngby, Dánia, 2010. június 20–23.,69–74. (cikk
megnyitása)
[8] Fódi A., Bódi I., The
effect of horizontal and vertical reinforcement on the shear capacity of masonry
walls, SEMC 2010, The 4th International Conference on Structural Engineering,
Mechanics and Computation, Cape Town, Dél-Afrika, 2010. szeptember 6-8.,
997–1000.
[9] Fódi A., Bódi I., Experimental investigation of solid masonry walls reinforced in different
directions, 8IMC 8th International Masonry Conference, 2010,
Drezda, Németország, 2010. július 4-7., 843–852. (cikk
megnyitása)
[10] Fódi A., Bódi I.,
Comparison of shear behaviour of masonry walls with and without reinforcement, POLLACK PERIODICA, 2010 5. kötet, 3. szám, 71–82. (cikk
megnyitása)
[11] Klouda J. K., Fódi A., Kubica J., Popescu R. &G., Bosiljkov V., Preparation for the Shear Wop at 8IMC on July 4, Region: MEE-Middle-East-Europe, Tanulmány a falazott szerkezetek alkalmazásáról Közép- és Kelet-Európában, Szerkesztette: V. Bosiljkov, 2010
[12] Fódi A., Bódi I., Basics
of reinforced masonry, Journal of CONCRETE STRUCTURES, 2011, 12. kötet (cikk
megnyitása)
[13] Fódi A., Effects influencing the compressive strength of a solid, fired clay brick, PERIODICA POLYTECHNICA Civil Engineering, 2011, (megjelenés alatt)
[14] Fódi A., Bódi I., The behaviour of a simplified micromodel for masonry, HCTAM, 2011, 11th Hungarian Conference on Theoretical and Applied Mechanics, Miskolc, 2011. augusztus 29-31. (megjelenés alatt)
[15] Fódi A., Kisméretű
téglából épített falazat tönkremeneteli módjának vizsgálata saját síkjában
történő nyírásra, Szemcsés anyagok mikromechanikája házi feladat, 2009 (cikk
megnyitása)
Linkgyűjtemény
Ezúton fejezem ki köszönetemet azoknak a cégeknek és magánszemélyeknek, akik a kutatási munka megvalósulásában segítséget nyújtottak és nyújtanak: a Wienerberger Zrt-nek, aki rendelkezésre bocsátotta a kísérletekhez szükséges anyagokat, az Itasca Consultants, S.A.S. nemzetközi szoftvergyártó cégnek, aki az Itasca Education Partnership Program keretén belül egy éves használatra rendelkezésemre bocsátotta a 3DEC háromdimenziós, diszkrét elemes modellezési programot
Hivatkozások
Abrams, D P, Masonry in the Americas, American Concrete Institute, SP-147, Detroit, Michigan, 1994.Amrhein, J E, Reinforced masonry engineering handbook, Masonry Institute of America, 1973.
Anderson, T L, Fracture mechanics, CRC Press, 1995
Andrejev, Sz A, Design and calculation of masonry structures, É.M. Építőipari könyv- és lapkiadó, Budapest, 1953
Árva, P, Sajtos, I, Determining of the condition of masonry failures with homogenisation, Abstract of the 10th Hungarian Conference for Mechanics (IUTAM), 2007. augusztus 27-29, 3.
Bagi, K, The discrete element method. Lecture notes, BME Tartószerkezetek Mechanikája Tanszék Budapest, 2007
Beamish, R, Memoir of the life of Sir Marc Isambard Brunel, civil engineer, vice-president of the Royal Society, corresponding member of the Institute of France, Longman, Green, Longman and Roberts, London
Bekaert, Murfor – Reinforcement for masonry, Product identification, range of applications, installation details, design principles, Szerkesztő: Timperman P., Bekaert, 2005
BEKAERT Specification: Murfor, reinforcement for brick work, AS-05-19, 2009-05-07.
Berto, L, Saetta, A, Scotta, R, Vitaliani, R, An orthotropic damage model for masonry structures, International Journal for Numerical Methods in Engineering, 127–157, 2002
Bojtár, I, Practical approach for fracture mechanics, Lecture notes, Budapest University of Technology, Department of Structural Mechanics, 2007
Chetouane, B, Dubois, F, Vinches, M, Bohatier, C, NSCD Discrete element method for modelling masonry structures, International Journal for Numerical Methods in Engineering, 64. kötet, 1. szám, 65–94, 2005
Crisafulli, J F, Seismic behaviour of reinforced concrete structures with masonry infills Doctoral dissertation. University of Canterbury, Christchurch, New Zealand, 1997
Csák, B, Hunyadi, F, Vértes, Gy, The effect of the earthquakes on buildings, Műszaki Könyvkiadó, Budapest, 1981
D’Ayala D F, Numerical modelling of masonry structures reinforced or repaired, Computer Methods in structural masonry –4, 161-168, 1998
Dulácska, E, Earthquake hazard, Protection against earthquakes, TT-TS 3, Logod Bt., (in Hungarian) MMK Logod Bt, Budapest, 2000
Dulácska E, The reconstruction and diagnostic of load bearing elements of buildings (Épületek tartószerkezeteinek diagnosztikája és rekonstrukciója), Jegyzet, 2008
Engineering Structures Research Centre, City University London, Low-rise residential construction detailing to resist earthquake, Repair & Strengthening of Brick/Block masonry, http://www.staff.city.ac.uk/earthquakes/Repairstrengthening/ index.php, Szerk.: Virdi, K. S. és Rashkoff, R. D., 2008. július 4.
Itasca, 3DEC 3 Dimensional Distinct Element Code Version 4.1, Online kézikönyv
Lourenço P B, Rots J G, Blaauwendraar J, Continuum models for masonry: Parameter estimation and validation, Journal of Structural Engineering, 642–652, 1998. június
Lourenço, P J B B, Computational strategies for masonry structures, Delft University Press Doctoral dissertation, Delft University Press, 1996
MI 15011-1988 Technical directive (Műszaki irányelv, Épületek megépült teherhordó szerkezeteinek erőtani vizsgálata), Hungarian Standard, Magyar Szabványügyi Hivatal
McKenzie WMC, Design of structural masonry, Palgrave, New York, 2. oldal, 2001
MSZ 15023-87, Design of load bearing masonry structures, Magyar Szabványügyi Hivatal (magyar nyelven), 1987. december 7
MSZ EN 1996-1-1:2006, Eurocode 6 - Design of masonry structures, Part 1-1: Common rules for reinforced and unreinforced masonry structures, 1. oldal, MSZT, Budapest, 2006. április
MSZ EN 772-1:2000 Methods of test masonry units Part 1: Determination of the compressive strength (Falazóelemek vizsgálati módszerei 1. rész: A nyomószilárdság meghatározása)
Pate K, Noble W, Stress-strain relationship in heavy clay products, in: Mechanical properties of non-metallic brittle materials, Butterworth, London, 1958, 210–216 Megjelent: Blight GE, Calculated Load bearing brickwork, Technical Publications, 2009, www.claybrick.org.za
Pluijm, Rvd, Non-linear behaviour of masonry under tension, HERON, 42. kötet, 1. szám, 25–54, 1997
Pluijm, Rvd, Shear behaviour of bed joints Proceedings of the 6th North American Masonry Conference, Szerk.: A.A. Hamid és H.G. Harris, Drexel University, Philadelphia, Pennsylvania, USA, 125–136, 1993
Reinhardt, H W, Brickwork, Jegyzet, Universität Stuttgart, Institut für Werkstoffe im Bauwesen, 1989
Rózsa, M, Rules for design of stone-, brick-, reinforced masonry and concrete structures, Felsőoktatási Jegyzetellátó Vállalat, Budapest, 1953
Sajtos, I, The Eurocode 6: Design principles and examples in: Balázs, L. Gy., Eurocode 6: Masonry Structures, Építésügyi Minőségellenőrző Közhasznú Társaság, Budapest, 47–84, 2001
Sajtos, I, Reinforced masonry structures – architectural and structural advantages, Építőmester, 2006. január-február, 24–25
Sajtos, I, Reinforced masonry structures, Építéstechnika, 40. oldal, 2006
Sajtos, I, Bed joint reinforced masonry structures, Építőmester, 2006. május-június, 36–37
Sajtos, I, Materials of masonry, szerk.: S. Fernezely, T. Matuscsák, Load bearing elements of structures, Actual constructional solutions for engineers, Chapter 6.4. Verlag Dashöfer Szakkiadó Kft és T. Bt, Budapest, 2004
Schneider, R R, Dickey, L W, Reinforced masonry design, 3. kiadás, Prentice Hall, Englewood Cliffs, New Jersey, 1994
Sieh-Beygi, B, Pietruszczak S, Numerical analysis of structural masonry mesoscale approach, Computers and Structures 86: 1958–1973, 2008
Subasic, C A, Borchelt J G, Clay and shale brick material properties – a statistical report, Proceedings of the 6th North American Masonry Conference, The masonry society, Boulder, CO, 1993, 12. oldal, Megjelent: Technical Notes 3A – Brick Masonry Material Properties, Technical notes on brick construction, 1992, www.gobrick.com
Zucchini, A, Lourenço P B, A micromechanical model for the homogenisation of masonry, International Journal of Solids and Structures, 3233–3255, 2002
Wienerberger Ltd, Application and design (in Hungarian), Budapest, 2009
